2024-06-26:用go语言,给定一个长度为n的数组nums和一个正整数k, 找到数组中所有相差绝对值恰好为k的子数组, 并返回这些子数组中元素之和的最大值。 如果找不到这样的子数组,返回0。 输
2024-06-26:用go语言,给定一个长度为n的数组nums和一个正整数k,
找到数组中所有相差绝对值恰好为k的子数组,
并返回这些子数组中元素之和的最大值。
如果找不到这样的子数组,返回0。
输入:nums = [-1,3,2,4,5], k = 3。
输出:11。
解释:好子数组中第一个元素和最后一个元素的差的绝对值必须为 3 。好子数组有 [-1,3,2] 和 [2,4,5] 。最大子数组和为 11 ,对应的子数组为 [2,4,5] 。
答案2024-06-26:
题目来自leetcode3026。
大体步骤如下:
1.初始化变量:设定初始答案 ans 为负无穷大(math.MinInt),创建一个空的 map minS 用来存储元素之和为某特定值的最小下标,初始化总和 sum 为 0。
2.遍历输入数组 nums:对于数组中的每个元素 x:
-
查找 x+k 是否在 minS 中,如果在,则更新 ans 为 sum + x - minS[x+k] 与 ans 的最大值。
-
查找 x-k 是否在 minS 中,如果在,则更新 ans 为 sum + x - minS[x-k] 与 ans 的最大值。
-
查找 x 是否在 minS 中,如果不存在或者 sum 小于 minS[x],则更新 minS[x] 为 sum。
-
更新当前总和 sum。
3.最终判断 ans 是否仍为负无穷大,如果是,则返回 0,否则将 ans 转换为 int64 类型后返回。
总的时间复杂度为 O(n),其中 n 为输入数组的长度。这是因为算法只需要一次遍历输入数组。
总的额外空间复杂度也是 O(n),因为使用了一个 map 来存储元素之和为特定值的最小下标,当输入数组中所有元素都不相差绝对值恰好为 k 时,map 中最多会存储 n 个元素。
Go完整代码如下:
package main
import (
"fmt"
"math"
)
func maximumSubarraySum(nums []int, k int) int64 {
ans := math.MinInt
minS := map[int]int{}
sum := 0
for _, x := range nums {
s, ok := minS[x+k]
if ok {
ans = max(ans, sum+x-s)
}
s, ok = minS[x-k]
if ok {
ans = max(ans, sum+x-s)
}
s, ok = minS[x]
if !ok || sum < s {
minS[x] = sum
}
sum += x
}
if ans == math.MinInt {
return 0
}
return int64(ans)
}
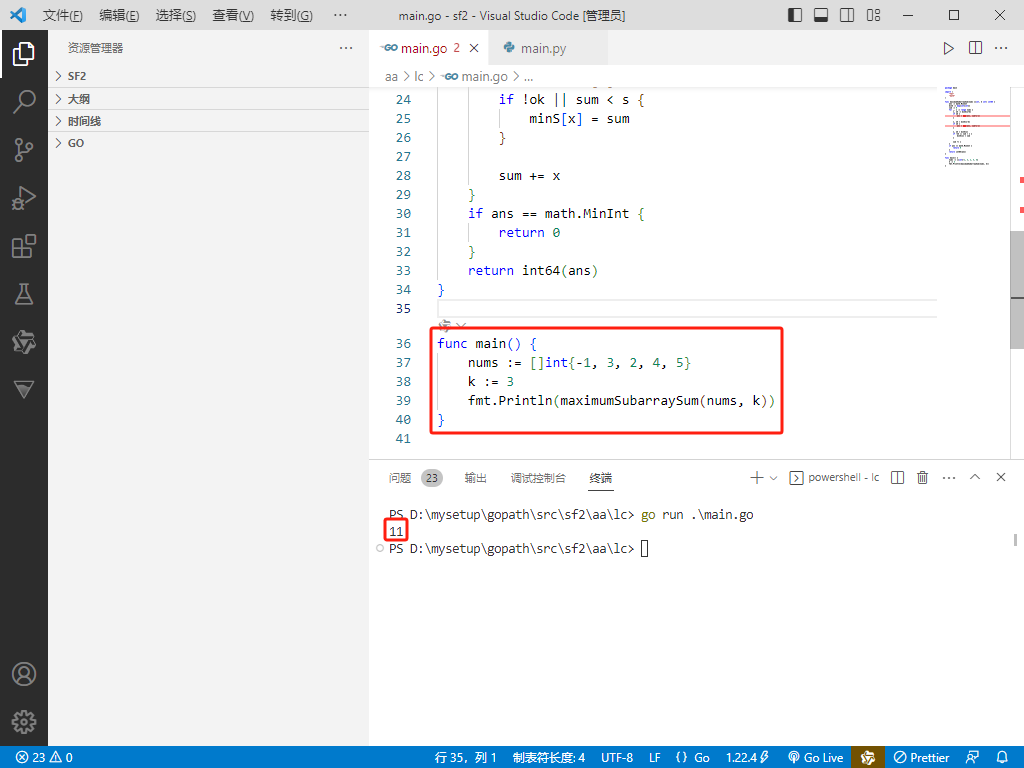
func main() {
nums := []int{-1, 3, 2, 4, 5}
k := 3
fmt.Println(maximumSubarraySum(nums, k))
}
Python完整代码如下:
# -*-coding:utf-8-*-
def maximum_subarray_sum(nums, k):
ans = float('-inf')
min_s = {}
sum_val = 0
for x in nums:
if x + k in min_s:
ans = max(ans, sum_val + x - min_s[x + k])
if x - k in min_s:
ans = max(ans, sum_val + x - min_s[x - k])
if x not in min_s or sum_val < min_s[x]:
min_s[x] = sum_val
sum_val += x
if ans == float('-inf'):
return 0
return ans
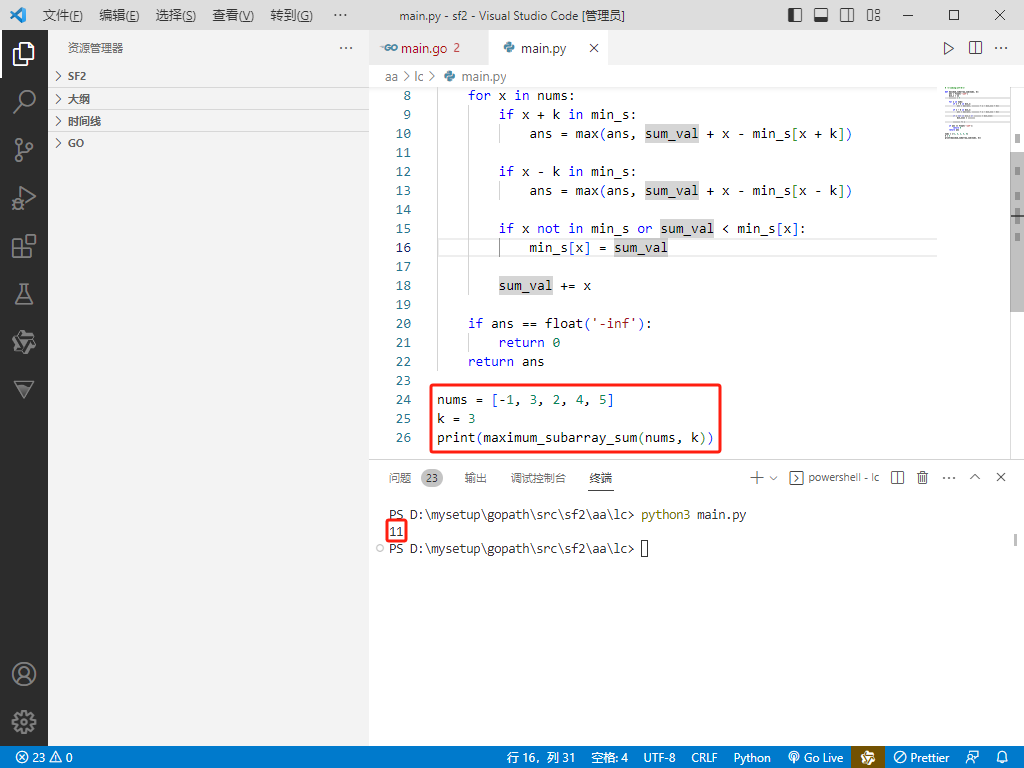
nums = [-1, 3, 2, 4, 5]
k = 3
print(maximum_subarray_sum(nums, k))
公众号:福大大架构师每日一题



 浙公网安备 33010602011771号
浙公网安备 33010602011771号