2024-05-22:用go语言,你有一个包含 n 个整数的数组 nums。 每个数组的代价是指该数组中的第一个元素的值。 你的目标是将这个数组划分为三个连续且互不重叠的子数组。 然后,计算这三个子数
2024-05-22:用go语言,你有一个包含 n 个整数的数组 nums。
每个数组的代价是指该数组中的第一个元素的值。
你的目标是将这个数组划分为三个连续且互不重叠的子数组。
然后,计算这三个子数组的代价之和,
要求返回这个和的最小值。
输入:nums = [1,2,3,12]。
输出:6。
答案2024-05-22:
题目来自leetcode3010。
大体步骤如下:
1.初始化操作:
-
从
main函数开始,创建一个整型数组nums,其中包含[1, 2, 3, 12]。 -
定义并调用
minimumCost函数来计算划分成三个子数组后的最小代价之和。
2.计算最小代价:
-
在
minimumCost函数中,fi和se被初始化为math.MaxInt64,表示两个最大的整数值,确保任何元素都会比它们小。 -
对于给定的数组
nums,迭代从第二个元素开始的所有元素:-
如果元素
x小于当前最小值fi,则将第二小值se更新为当前最小值fi,并更新最小值为x。 -
否则,如果元素
x介于当前最小值fi和第二小值se之间,则更新第二小值se为x。
-
-
返回结果为数组第一个元素
nums[0]与找到的两个最小值fi和se的和。
3.解问题:
-
对于输入数组
[1, 2, 3, 12],算法将找到两个最小值为1和2。 -
算法返回结果为
1 + 1 + 2 = 4,此结果表示划分三个子数组后的最小代价之和。
4.时间复杂度:
- 迭代一次数组,需要
O(n)的时间复杂度,其中n是数组的长度。
5.空间复杂度:
- 除了输入的数组外,算法只使用了常量级别的额外空间,因此空间复杂度为
O(1)。
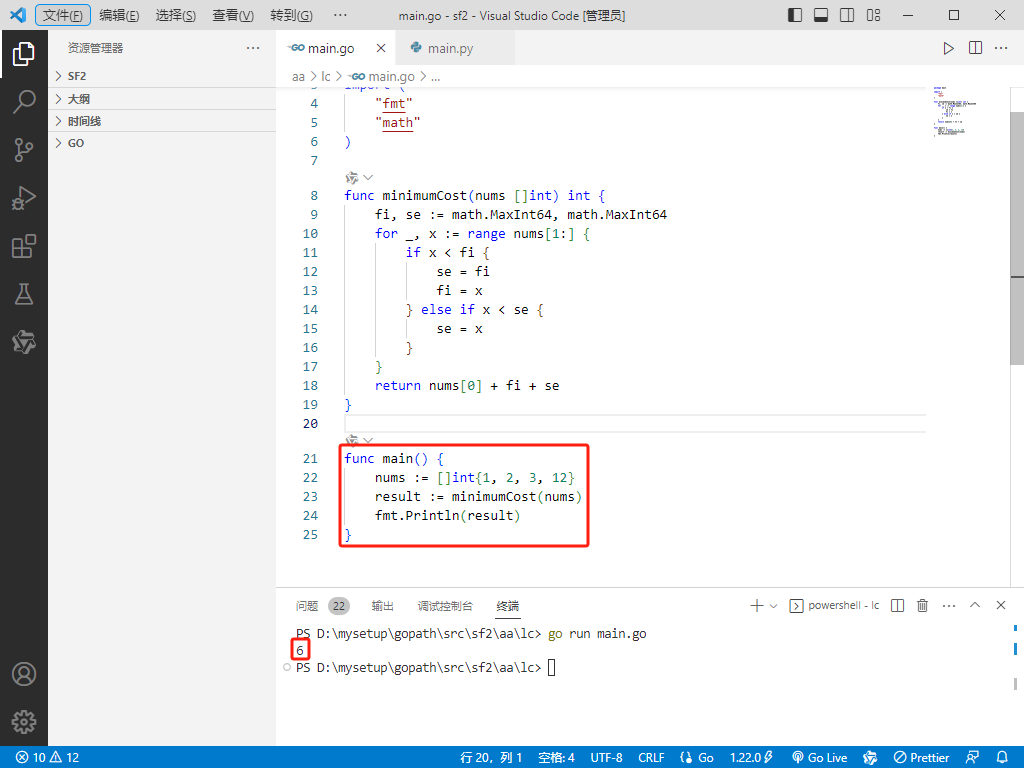
Go完整代码如下:
package main
import (
"fmt"
"math"
)
func minimumCost(nums []int) int {
fi, se := math.MaxInt64, math.MaxInt64
for _, x := range nums[1:] {
if x < fi {
se = fi
fi = x
} else if x < se {
se = x
}
}
return nums[0] + fi + se
}
func main() {
nums := []int{1, 2, 3, 12}
result := minimumCost(nums)
fmt.Println(result)
}
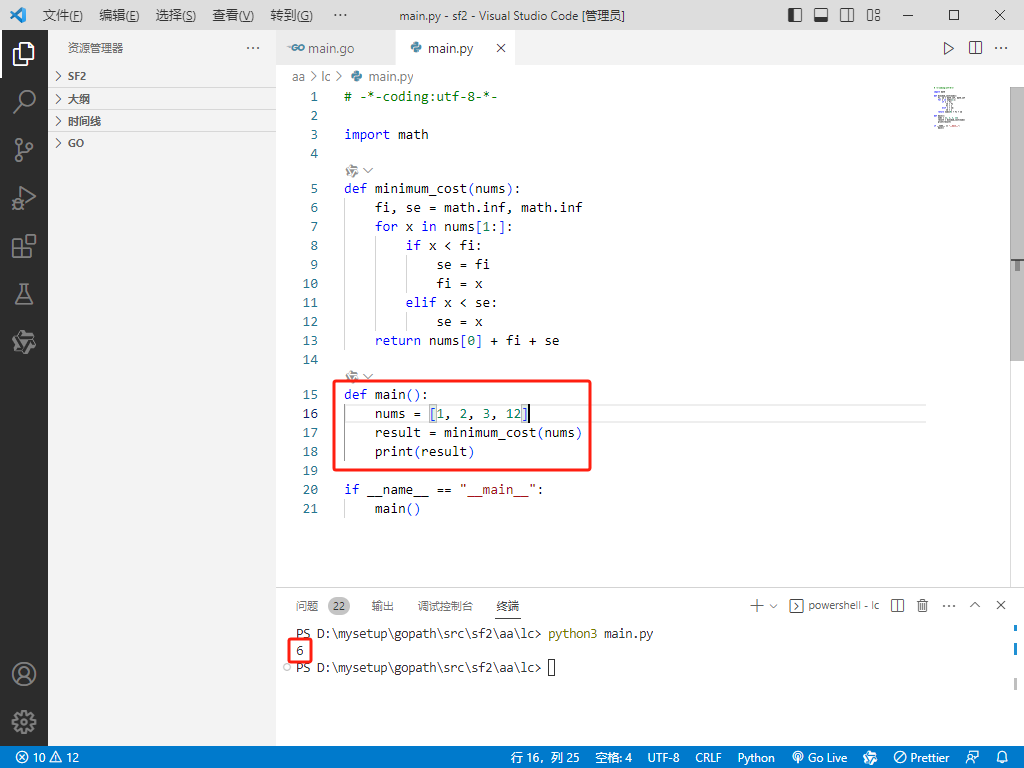
Python完整代码如下:
# -*-coding:utf-8-*-
import math
def minimum_cost(nums):
fi, se = math.inf, math.inf
for x in nums[1:]:
if x < fi:
se = fi
fi = x
elif x < se:
se = x
return nums[0] + fi + se
def main():
nums = [1, 2, 3, 12]
result = minimum_cost(nums)
print(result)
if __name__ == "__main__":
main()
公众号:福大大架构师每日一题



 浙公网安备 33010602011771号
浙公网安备 33010602011771号