2024-04-13：用go语言，给定一个整数数组 `nums`， 请编写一个函数，返回一个新的数组 `counts`。 满足以下条件：对于每个 `nums[i]`， `counts[i]` 表示在

2024-04-13：用go语言，给定一个整数数组 nums，

请编写一个函数，返回一个新的数组 counts。

满足以下条件：对于每个 nums[i]，

counts[i] 表示在 nums[i] 右侧且比nums[i] 小的元素数量。

输入：nums = [5,2,6,1]。

输出：[2,1,1,0] 。

答案2024-04-13：

来自左程云。

灵捷3.5

大体过程如下：

给定一个整数数组 nums，首先创建一个与 nums 大小相同的临时数组 sorted，并将 nums 的元素复制到 sorted 中。然后对 sorted 进行排序，得到按升序排列的新数组。

接下来，创建一个映射 rank，用于记录每个数在排序后数组中的排名。遍历排序后的数组，将排名存储到 rank 中。注意，排名从1开始。

接着创建一个 bit 数组，长度为 n+2，并定义一个函数 lowbit，它可以计算一个数的二进制表示中最低位的1的值。再定义一个函数 query，用于查询比给定排名小的元素数量。函数内部使用循环将 bit 数组的前缀和累加到结果中，直到排名为0。还定义一个函数 update，用于更新 bit 数组中对应排名的计数值。

然后创建一个结果数组 ans，初始化为全0。从右向左遍历原始数组 nums，获取当前元素在排序后数组中的排名 r，通过调用 query 函数获得在当前元素右侧且小于它的元素数量，并将结果存储到 ans 中。同时，调用 update 函数更新 bit 数组中排名为 r 的计数值。

最后返回结果数组 ans。

总的时间复杂度为O(nlogn)，其中n为数组的大小，主要由排序操作决定。总的额外空间复杂度为O(n)，用于存储临时数组和映射等辅助空间。

Go完整代码如下：

package main

import (
	"fmt"
	"sort"
)

func countSmaller(nums []int) []int {
	n := len(nums)
	sorted := make([]int, n)
	copy(sorted, nums)
	sort.Ints(sorted)
	rank := make(map[int]int)
	for i, num := range sorted {
		rank[num] = i + 1
	}

	bit := make([]int, n+2)
	lowbit := func(x int) int {
		return x & -x
	}

	query := func(x int) int {
		res := 0
		for x > 0 {
			res += bit[x]
			x -= lowbit(x)
		}
		return res
	}

	update := func(x int) {
		for x <= n+1 {
			bit[x]++
			x += lowbit(x)
		}
	}

	ans := make([]int, n)
	for i := n - 1; i >= 0; i-- {
		r := rank[nums[i]]
		ans[i] = query(r - 1)
		update(r)
	}
	return ans
}

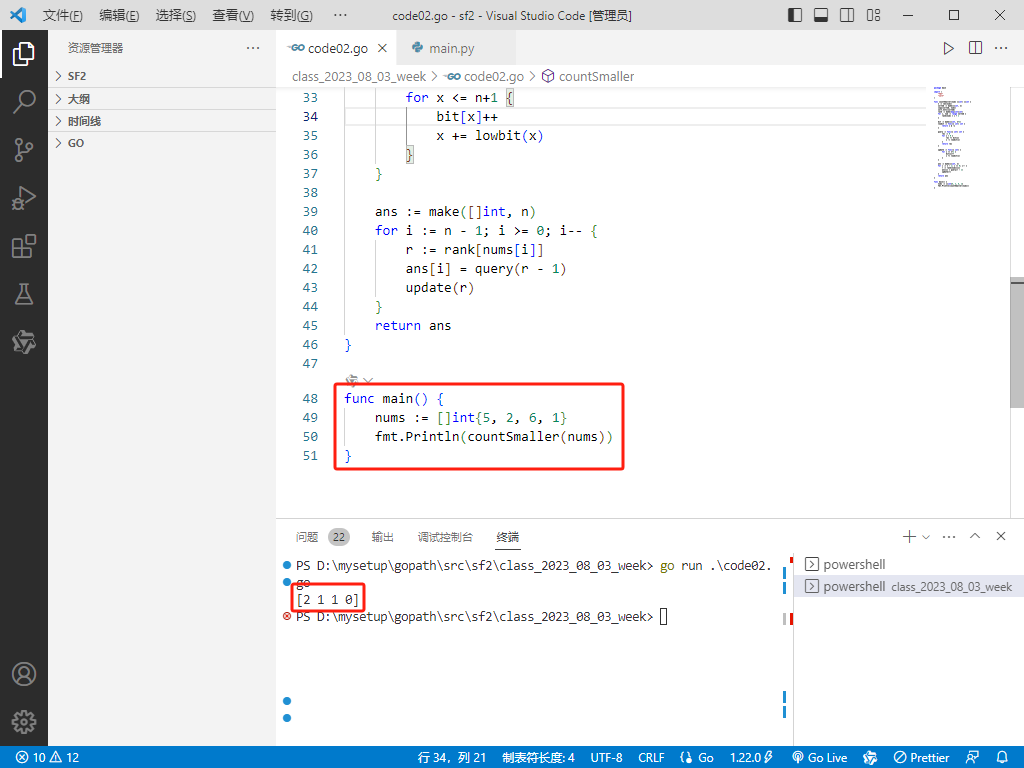
func main() {
	nums := []int{5, 2, 6, 1}
	fmt.Println(countSmaller(nums))
}

Python完整代码如下：

# -*-coding:utf-8-*-

def count_smaller(nums):
    n = len(nums)
    sorted_nums = sorted([(num, i) for i, num in enumerate(nums)])
    rank = {sorted_nums[i][0]: i + 1 for i in range(n)}
    
    bit = [0] * (n+2)
    
    def lowbit(x):
        return x & -x
    
    def query(x):
        res = 0
        while x > 0:
            res += bit[x]
            x -= lowbit(x)
        return res
    
    def update(x):
        while x <= n + 1:
            bit[x] += 1
            x += lowbit(x)
    
    ans = [0] * n
    for i in range(n-1, -1, -1):
        r = rank[nums[i]]
        ans[i] = query(r - 1)
        update(r)
    return ans

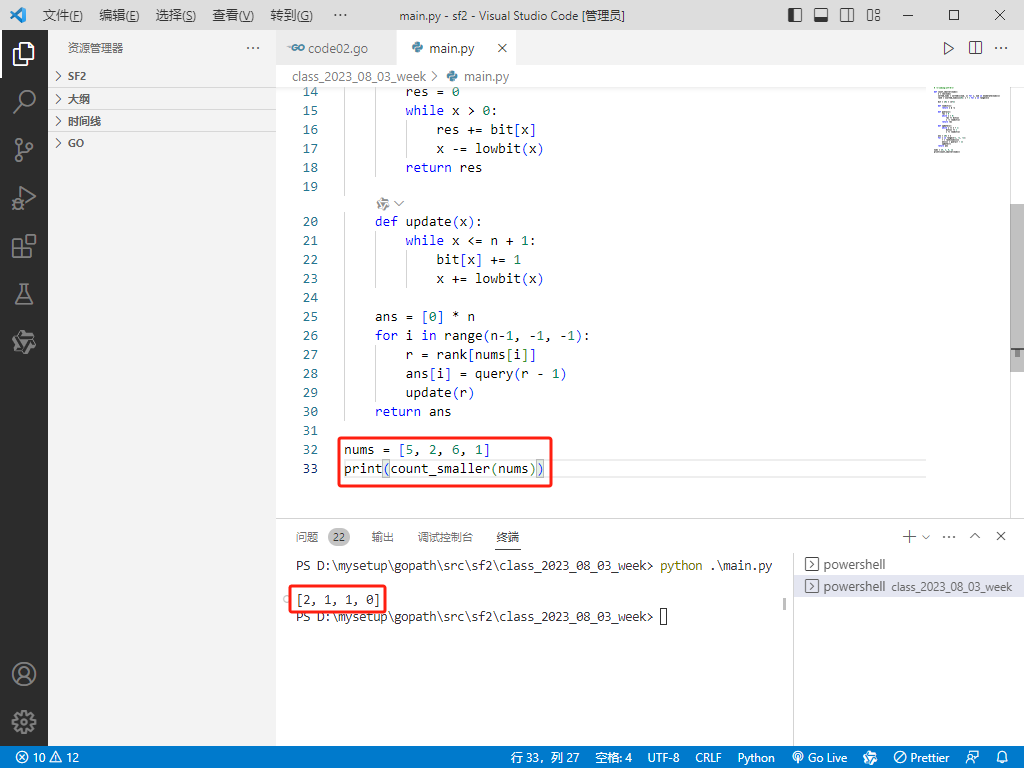
nums = [5, 2, 6, 1]
print(count_smaller(nums))