2024-04-10:用go语言,考虑一个非负整数数组 A, 如果数组中相邻元素之和为完全平方数,我们称这个数组是正方形数组。 现在要计算 A 的正方形排列的数量。 两个排列 A1 和 A2 被认为是
2024-04-10:用go语言,考虑一个非负整数数组 A,
如果数组中相邻元素之和为完全平方数,我们称这个数组是正方形数组。
现在要计算 A 的正方形排列的数量。
两个排列 A1 和 A2 被认为是不同的,如果存在至少一个索引 i,满足 A1[i] != A2[i]。
输入:[1,17,8]。
输出:2。
答案2024-04-10:
来自左程云。
大体过程如下:
1.定义变量和数据结构:
-
定义常量
MAXN为 13,表示数组的最大长度。 -
定义全局变量
f,存储阶乘的预计算结果。
2.编写初始化函数 init():
-
创建长度为
MAXN的切片f,并将其第一个元素初始化为 1。 -
使用循环计算并预存每个阶乘值。
3.编写函数 numSquarefulPerms(nums []int) int 来计算正方形排列的数量:
-
初始化变量
n为数组nums的长度。 -
创建二维切片
graph和dp,分别用于记录数字之间是否存在完全平方数关系和动态规划的状态。 -
遍历数组
nums构建图graph,找出数字之间的完全平方数关系。 -
初始化变量
ans为 0,用于记录正方形排列的数量。 -
使用深度优先搜索函数
dfs()遍历图graph,并计算正方形排列的数量。 -
将数组
nums进行排序,以便处理相同数字的情况。 -
使用变量
start和end遍历排序后的数组nums,计算相同数字之间的排列数量,并更新结果。 -
返回最终的正方形排列数量。
4.编写深度优先搜索函数 dfs(graph [][]int, i int, s int, n int, dp [][]int) int:
-
如果当前状态
s表示所有元素都被使用,返回1,表示找到了一种满足条件的排列。 -
如果当前状态已经被计算过,直接返回对应的结果。
-
初始化变量
ans为 0,用于记录满足条件的排列数量。 -
遍历与当前位置
i相邻的下一个位置next:-
如果下一个位置
next还未被包含在当前状态s中,将其加入到状态s中,并递归调用dfs()继续搜索。 -
将递归调用的结果累加到变量
ans中。
-
-
将结果存储到
dp中,并返回。
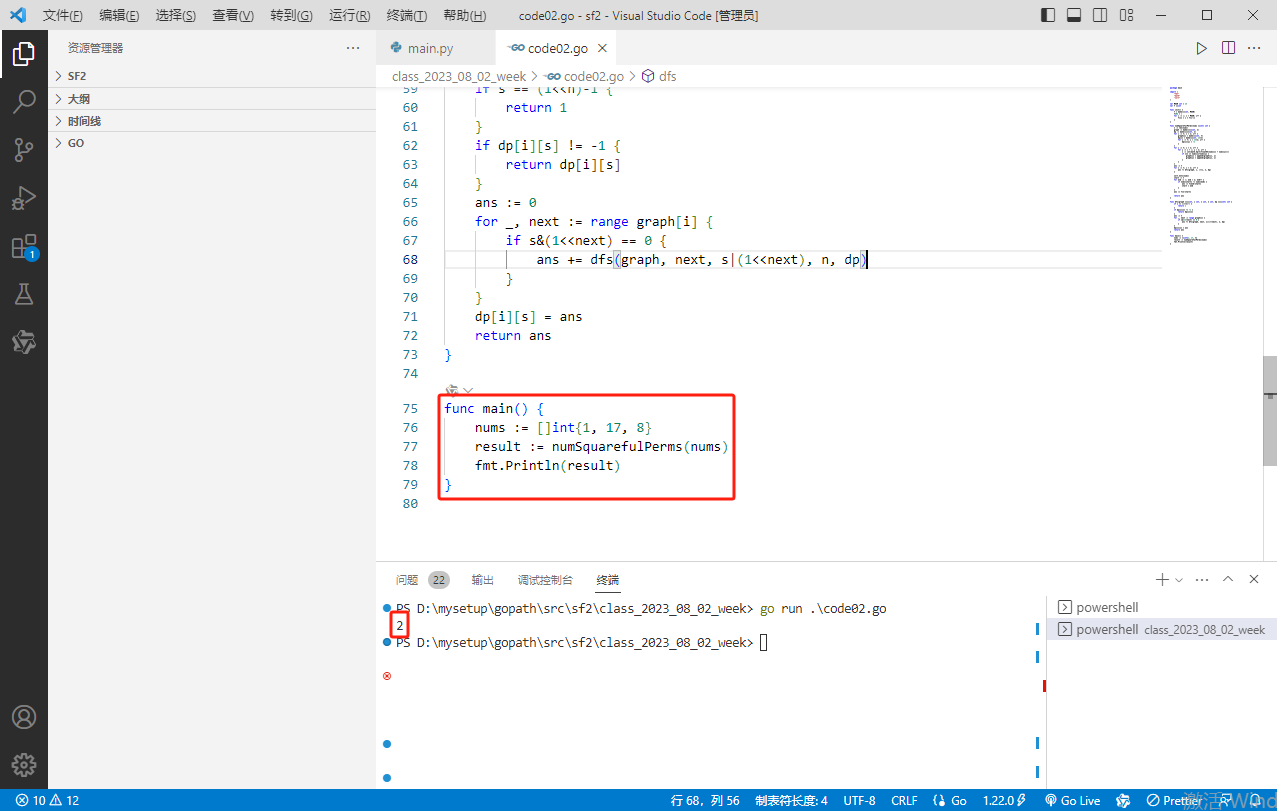
5.在 main() 函数中调用 numSquarefulPerms(),传入示例数据 [1, 17, 8],并打印结果。
总的时间复杂度:O(n * n!)
-
预计算阶乘的时间复杂度为 O(MAXN) = O(1),因为 MAXN 是常数。
-
构建图和计算正方形排列的数量的时间复杂度为 O(n!),其中 n 是数组
nums的长度。 -
数组排序的时间复杂度为 O(n * logn),其中 n 是数组
nums的长度。
总的空间复杂度:O(n * 2^n)
-
动态规划的状态数组
dp的空间复杂度为 O(n * 2^n),其中 n 是数组nums的长度。 -
构建图的辅助数组
graph的空间复杂度为 O(n^2),其中 n 是数组nums的长度。 -
其他变量和数据结构的空间复杂度为 O(1)。
Go完整代码如下:
package main
import (
"fmt"
"math"
"sort"
)
var MAXN int = 13
var f []int
func init() {
f = make([]int, MAXN)
f[0] = 1
for i := 1; i < MAXN; i++ {
f[i] = i * f[i-1]
}
}
func numSquarefulPerms(nums []int) int {
n := len(nums)
graph := make([][]int, n)
dp := make([][]int, n)
for i := 0; i < n; i++ {
graph[i] = make([]int, 0)
dp[i] = make([]int, 1<<n)
for j := 0; j < 1<<n; j++ {
dp[i][j] = -1
}
}
for i := 0; i < n; i++ {
for j := i + 1; j < n; j++ {
s := int(math.Sqrt(float64(nums[i] + nums[j])))
if s*s == nums[i]+nums[j] {
graph[i] = append(graph[i], j)
graph[j] = append(graph[j], i)
}
}
}
ans := 0
for i := 0; i < n; i++ {
ans += dfs(graph, i, 1<<i, n, dp)
}
sort.Ints(nums)
start := 0
for end := 1; end < n; end++ {
if nums[start] != nums[end] {
ans /= f[end-start]
start = end
}
}
ans /= f[n-start]
return ans
}
func dfs(graph [][]int, i int, s int, n int, dp [][]int) int {
if s == (1<<n)-1 {
return 1
}
if dp[i][s] != -1 {
return dp[i][s]
}
ans := 0
for _, next := range graph[i] {
if s&(1<<next) == 0 {
ans += dfs(graph, next, s|(1<<next), n, dp)
}
}
dp[i][s] = ans
return ans
}
func main() {
nums := []int{1, 17, 8}
result := numSquarefulPerms(nums)
fmt.Println(result)
}
Python完整代码如下:
# -*-coding:utf-8-*-
import math
from collections import defaultdict
MAXN = 13
f = [0] * MAXN
def init():
global f
f[0] = 1
for i in range(1, MAXN):
f[i] = i * f[i-1]
def numSquarefulPerms(nums):
n = len(nums)
graph = defaultdict(list)
dp = [[-1 for _ in range(1<<n)] for _ in range(n)]
for i in range(n):
for j in range(i + 1, n):
s = int((nums[i] + nums[j]) ** 0.5)
if s * s == nums[i] + nums[j]:
graph[i].append(j)
graph[j].append(i)
def dfs(i, s):
if s == (1<<n) - 1:
return 1
if dp[i][s] != -1:
return dp[i][s]
ans = 0
for next in graph[i]:
if s & (1 << next) == 0:
ans += dfs(next, s | (1 << next))
dp[i][s] = ans
return ans
ans = 0
for i in range(n):
ans += dfs(i, 1 << i)
nums.sort()
start = 0
for end in range(1, n):
if nums[start] != nums[end]:
ans //= f[end - start]
start = end
ans //= f[n - start]
return ans
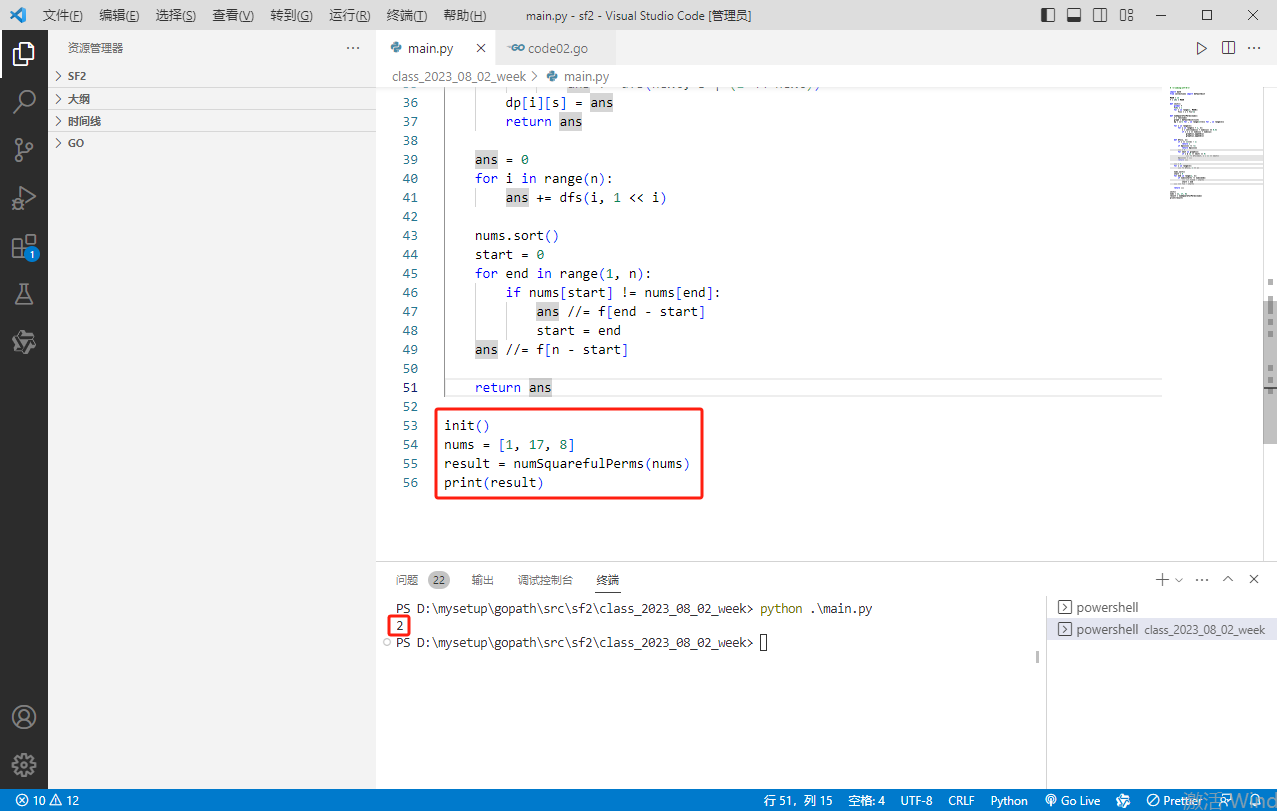
init()
nums = [1, 17, 8]
result = numSquarefulPerms(nums)
print(result)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号