2024-04-06:用go语言,给你两个非负整数数组 rowSum 和 colSum, 其中 rowSum[i] 是二维矩阵中第 i 行元素的和, colSum[j] 是第 j 列元素的和,换言之你
2024-04-06:用go语言,给你两个非负整数数组 rowSum 和 colSum,
其中 rowSum[i] 是二维矩阵中第 i 行元素的和,
colSum[j] 是第 j 列元素的和,换言之你不知道矩阵里的每个元素,
但是你知道每一行和每一列的和。
请找到大小为 rowSum.length x colSum.length 的任意 非负整数 矩阵。
且该矩阵满足 rowSum 和 colSum 的要求。
请你返回任意一个满足题目要求的二维矩阵,题目保证存在 至少一个 可行矩阵。
输入:rowSum = [3,8], colSum = [4,7]。
输出:[[3,0],[1,7]]。
答案2024-04-06:
来自左程云。
大体步骤如下:
1.初始化一个大小为rowSum.length x colSum.length的二维矩阵ans,用于存储最终的结果。
2.遍历rowSum数组,对于每个元素rowSum[i],继续遍历colSum数组,对于每个元素colSum[j]:
-
将ans[i][j]设为rowSum[i]和colSum[j]中的较小值,即ans[i][j] = min(rowSum[i], colSum[j])。
-
更新rowSum[i]和colSum[j],分别减去已经分配的值ans[i][j],即rowSum[i] -= ans[i][j],colSum[j] -= ans[i][j]。
3.返回ans作为结果矩阵。
总的时间复杂度:遍历rowSum和colSum数组需要$O(n2)$的时间复杂度,其中n是rowSum和colSum的长度。因此,总的时间复杂度为$O(n2)$。
总的额外空间复杂度:额外使用了一个二维矩阵ans来存储结果,其大小为rowSum.length x colSum.length,因此总的额外空间复杂度为$O(n^2)$。
Go完整代码如下:
package main
import (
"fmt"
)
func restoreMatrix(rowSum []int, colSum []int) [][]int {
n := len(rowSum)
m := len(colSum)
ans := make([][]int, n)
for i := 0; i < n; i++ {
ans[i] = make([]int, m)
for j := 0; j < m; j++ {
ans[i][j] = min(rowSum[i], colSum[j])
rowSum[i] -= ans[i][j]
colSum[j] -= ans[i][j]
}
}
return ans
}
func min(a, b int) int {
if a < b {
return a
}
return b
}
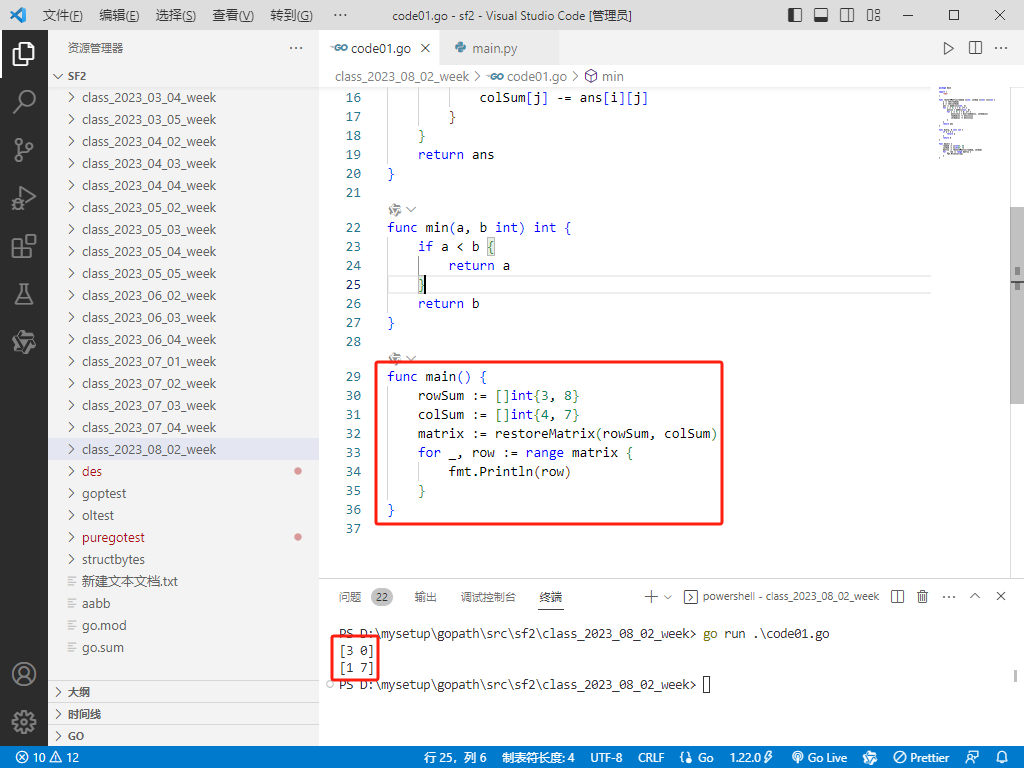
func main() {
rowSum := []int{3, 8}
colSum := []int{4, 7}
matrix := restoreMatrix(rowSum, colSum)
for _, row := range matrix {
fmt.Println(row)
}
}
Python完整代码如下:
# -*-coding:utf-8-*-
def restoreMatrix(rowSum, colSum):
n = len(rowSum)
m = len(colSum)
ans = [[0] * m for _ in range(n)]
for i in range(n):
for j in range(m):
ans[i][j] = min(rowSum[i], colSum[j])
rowSum[i] -= ans[i][j]
colSum[j] -= ans[i][j]
return ans
def min(a, b):
if a < b:
return a
return b
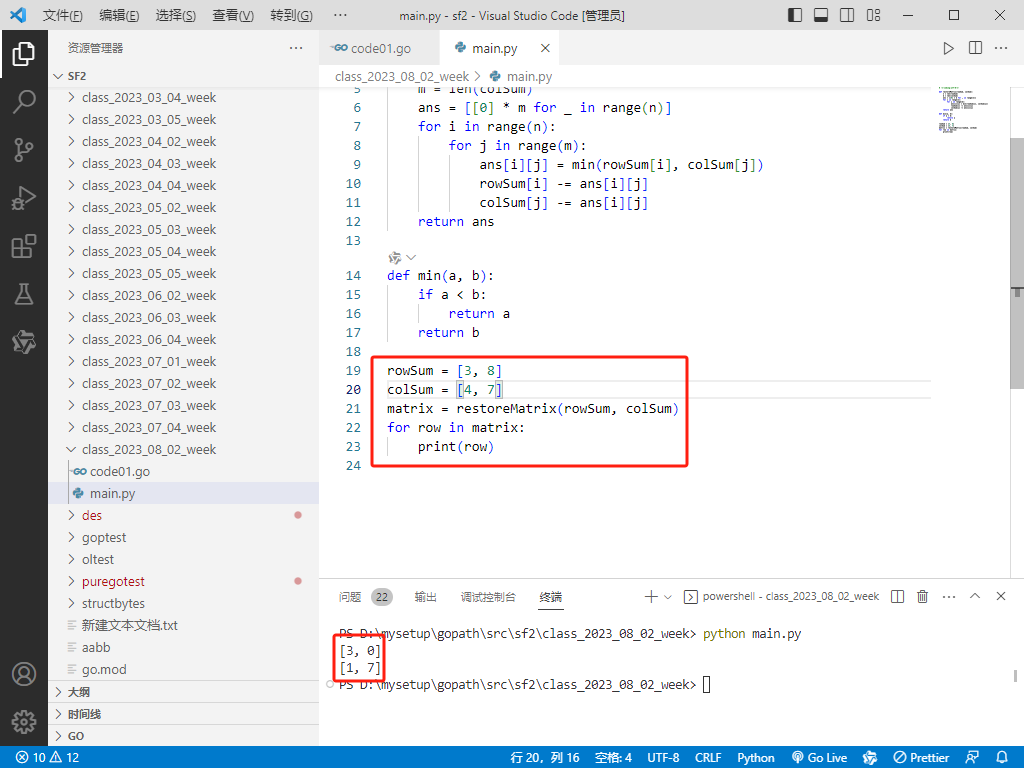
rowSum = [3, 8]
colSum = [4, 7]
matrix = restoreMatrix(rowSum, colSum)
for row in matrix:
print(row)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号