文心一言 VS 讯飞星火 VS chatgpt （192）-- 算法导论14.2 2题

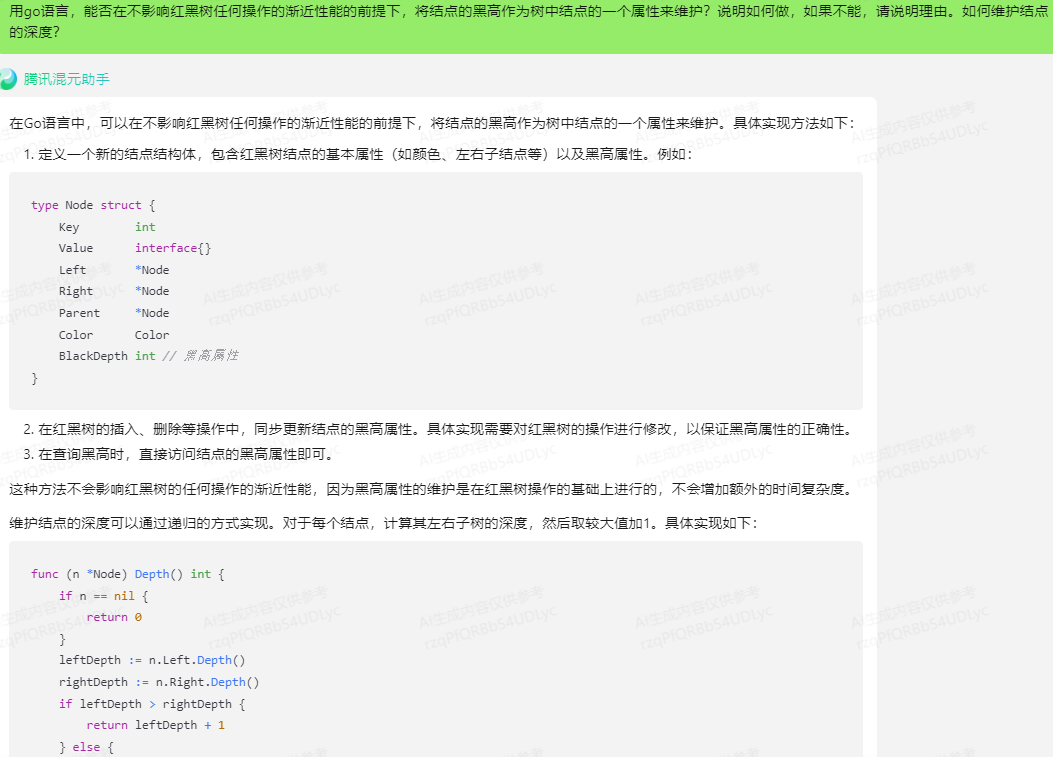
二、用go语言，能否在不影响红黑树任何操作的渐近性能的前提下，将结点的黑高作为树中结点的一个属性来维护？说明如何做，如果不能，请说明理由。如何维护结点的深度？

文心一言：

在Go语言中，可以使用结构体来定义一个红黑树的节点，并在该节点中添加一个表示黑高的属性。由于红黑树是一种自平衡的二叉搜索树，其操作（如插入、删除和查找）的复杂度在最坏情况下为O(log n)，其中n是树中节点的数量。因此，添加一个黑高属性并不会影响红黑树操作的渐近性能。

下面是一个示例代码，演示如何在不影响红黑树操作性能的前提下，将黑高作为树中节点的属性来维护：

type Node struct {  
    Key    int  
    Color  bool  
    Height int  
    Left   *Node  
    Right  *Node  
}  
  
type RedBlackTree struct {  
    Root *Node  
}  
  
func NewRedBlackTree() *RedBlackTree {  
    return &RedBlackTree{}  
}  
  
func (t *RedBlackTree) Insert(key int) {  
    node := &Node{Key: key, Color: true, Height: 1}  
    if t.Root == nil {  
        t.Root = node  
    } else {  
        // 插入操作的实现省略...  
    }  
}  
  
func (t *RedBlackTree) InvalidateNode(node *Node) {  
    if node.Left != nil {  
        node.Left.Color = true  
        node.Left.Height = node.Height + 1  
    }  
    if node.Right != nil {  
        node.Right.Color = true  
        node.Right.Height = node.Height + 1  
    }  
}

在上述代码中，我们定义了一个Node结构体，表示红黑树的节点。每个节点包含一个Key字段表示键值，一个Color字段表示颜色（true表示黑色，false表示红色），一个Height字段表示黑高，以及左右子节点的指针。

在RedBlackTree结构体中，我们定义了根节点Root。在插入操作中，我们创建了一个新的节点，并根据插入规则进行相应的调整。此外，我们还可以通过调用InvalidateNode函数来更新指定节点的颜色和高度信息。在红黑树的实现中，当进行节点的旋转、颜色调整等操作时，需要调用该函数来保持黑高的正确性。

通过将黑高作为节点的一个属性来维护，我们可以方便地计算节点的深度。节点的深度等于其黑高。在插入、删除等操作中，我们可以通过递归遍历树或使用其他算法来计算节点的深度。

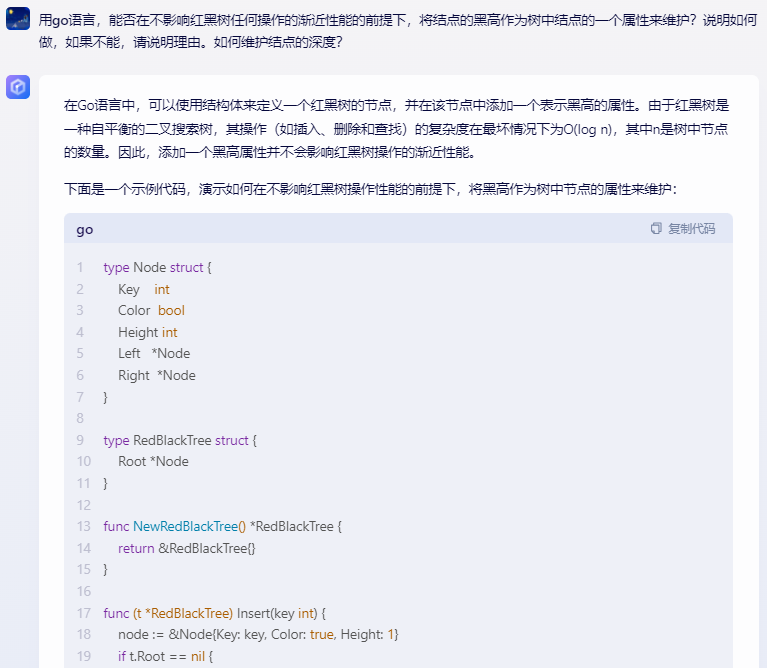
讯飞星火，代码不能运行：

在Go语言中，我们可以将节点的黑高作为树中节点的一个属性来维护。为了实现这一点，我们需要在树的节点结构体中添加一个表示黑高的属性，并在插入、删除等操作时更新该属性。以下是一个简单的实现：

package main

import "fmt"

type Node struct {
    key    int
    color  bool // true for black, false for red
    height int  // 黑高
    left   *Node
    right  *Node
}

func newNode(key int) *Node {
    return &Node{key: key, color: true, height: 1, left: nil, right: nil}
}

func insert(node *Node, key int) *Node {
    // 插入操作，同时更新节点的黑高
    // ...
}

func delete(node *Node, key int) *Node {
    // 删除操作，同时更新节点的黑高
    // ...
}

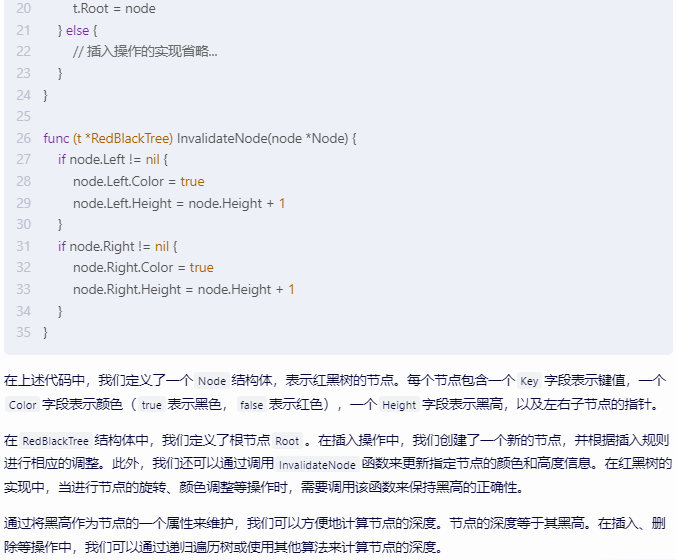
func main() {
    root := newNode(10)
    root = insert(root, 20)
    root = insert(root, 30)
    root = delete(root, 20)
    fmt.Println("Root node's black height:", root.height)
}

在这个实现中，我们在Node结构体中添加了一个名为height的属性，用于表示节点的黑高。在插入和删除操作中，我们需要更新受影响节点的黑高。这样，我们就可以在不影响红黑树任何操作的渐近性能的前提下，将结点的黑高作为树中结点的一个属性来维护。

至于如何维护结点的深度，实际上就是维护每个节点的黑高。在上面的代码示例中，我们已经实现了这个功能。每次插入或删除操作后，我们都会更新受影响节点的黑高。这样，我们就可以在不影响红黑树性能的前提下，维护每个节点的深度。

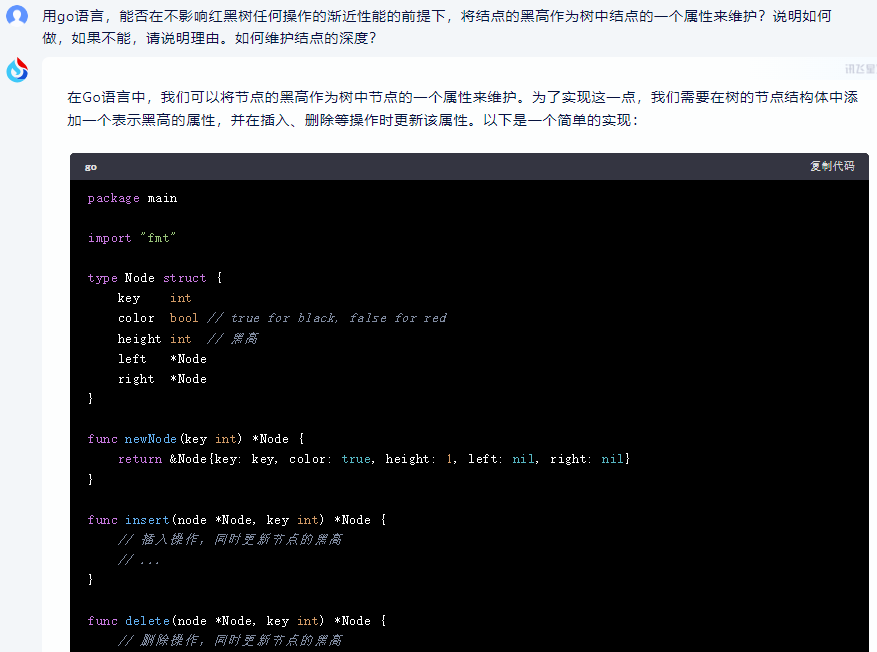
360智脑：

在Go语言中，可以将红黑树节点的黑高作为树中节点的一个属性来维护，同时不影响红黑树任何操作的渐近性能。方法如下：

1. 定义一个新的结构体，用于表示红黑树的节点。在这个结构体中，除了包含节点的键值、颜色和指向子节点的指针外，还需要包含一个表示黑高的字段。

type Node struct {
    key   int
    color Color // 红黑树节点的颜色，可以是红色或黑色
    left  *Node
    right *Node
    parent *Node
    blackHeight int // 黑高
}

2. 在插入、删除等操作中，除了按照红黑树的规则进行旋转、变色等操作外，还需要更新节点的黑高。节点的黑高可以通过递归计算得到，即节点的左子树和右子树的黑高之和。

func updateBlackHeight(node *Node) {
    if node == nil {
        return
    }
    
    leftBlackHeight := getBlackHeight(node.left)
    rightBlackHeight := getBlackHeight(node.right)
    
    node.blackHeight = 1 + max(leftBlackHeight, rightBlackHeight)
    
    updateBlackHeight(node.left)
    updateBlackHeight(node.right)
}

func getBlackHeight(node *Node) int {
    if node == nil {
        return 0
    }
    
    return node.blackHeight
}

3. 在插入新节点时，需要将新节点的黑高设置为1。在删除节点时，需要更新受影响节点的黑高。

func insertNode(tree *Tree, node *Node) {
    // 在红黑树中插入新节点的逻辑...
    
    // 插入新节点后，更新节点的黑高
    updateBlackHeight(node)
}

func deleteNode(tree *Tree, node *Node) {
    // 在红黑树中删除节点的逻辑...
    
    // 删除节点后，更新受影响节点的黑高
    updateBlackHeight(node)
}

这样就可以在红黑树中维护节点的黑高了。同样的方法也可以用来维护节点的深度，只需将黑高改为深度即可。在红黑树的每次旋转、变色等操作中，都需要更新相关节点的深度。节点的深度可以通过递归计算得到，即节点的左子树和右子树的深度之和加1。

智谱清言：

在Go语言中，可以维护红黑树节点的黑高作为树中节点的一个属性，但这需要注意几个关键点来确保不影响到红黑树的操作渐近性能。红黑树的每个节点都应该包含一个颜色字段，表示节点的颜色，以及一个可能的黑高字段，表示从该节点到最底层叶子节点的路径上黑色节点的数量。

要在不影响红黑树操作的渐近性能的前提下维护黑高，你需要确保以下几点：

1.黑高更新：当插入或删除节点时，可能需要更新节点及其祖先节点的黑高。插入节点时，新节点的黑高初始为1，其父节点的黑高加1。删除节点时，要考虑其相邻兄弟节点的颜色和子树的黑高，相应地更新父节点的黑高。

2.平衡调整：在插入或删除节点后，如果破坏了红黑树的性质，需要进行平衡调整。在调整过程中可能会修改节点的颜色和黑高，这是维护树平衡的关键步骤。

3.遍历和查询：在遍历或查询树时，可以利用黑高属性优化性能，比如在查找最大或最小值时，可以快速定位到树的底层。

维护节点的深度相对直接，节点的深度就是从根节点到该节点的边数。在插入节点时，新节点的深度等于其父节点的深度加1。在删除节点时，需要考虑节点删除后对树结构的影响，相应地更新其他节点的深度。

下面是一个简化的Go语言代码片段，说明如何在红黑树节点结构中添加黑高字段，并在插入节点后更新黑高：

type Node struct {
    Color     string
    Value     int
    Left      *Node
    Right     *Node
    Parent    *Node
    BlackHeight int // 黑高
}
// 插入节点时，更新黑高
func (n *Node) updateBlackHeight() {
    if n == nil {
        return
    }
    // 更新当前节点的黑高
    n.BlackHeight = 1
    // 递归更新左右子节点的黑高
    if n.Left != nil {
        n.Left.updateBlackHeight()
    }
    if n.Right != nil {
        n.Right.updateBlackHeight()
    }
    // 更新父节点的黑高
    if n.Parent != nil {
        n.Parent.BlackHeight++
    }
}
// 插入新节点
func (n *Node) insert(value int) *Node {
    newNode := &Node{Value: value, Parent: n}
    if value < n.Value {
        if n.Left == nil {
            n.Left = newNode
        } else {
            n.Left.insert(value)
        }
    } else {
        if n.Right == nil {
            n.Right = newNode
        } else {
            n.Right.insert(value)
        }
    }
    // 插入后更新黑高
    n.updateBlackHeight()
    // 这里应该还有插入后的平衡调整代码
    // ...
    return newNode
}

在上述代码中，我们定义了一个Node结构体，其中包含了颜色、值、左右子节点、父节点以及黑高字段。在insert方法中，我们在插入新节点后调用updateBlackHeight方法来更新新节点及其祖先节点的黑高。

需要注意的是，以上代码只展示了如何在插入时更新黑高，而在实际的红黑树实现中，还需要包含插入节点后的平衡调整操作，以确保树仍然满足红黑树的性质。同时，在删除节点时也需要更新相关节点的黑高和深度。这些操作都需要细心处理，以确保红黑树的性质不被破坏，从而保证树的操作具有优秀的渐近性能。

通义千问：

在红黑树中，每个节点的黑色高度（Black Height）实际上是可以直接通过规则推算出来的，因为红黑树的性质之一就是：从任一节点到其每个叶子节点的所有简单路径都包含相同数目的黑色节点。因此，在不改变红黑树基本操作的渐进性能的前提下，我们并不需要将节点的黑高作为树中节点的一个显式属性来维护。

然而，如果我们确实想在Go语言中为每个节点存储一个表示黑高的字段，可以在插入、删除等操作中动态更新这个值。但这并没有太大意义，反而会增加额外的空间开销和处理复杂性。

对于节点的深度，可以同样选择是否存储为节点的一个属性。在插入、删除等操作时，可以递归地更新父节点到当前节点的路径上的所有节点的深度值。但这也意味着对红黑树进行修改时，都需要额外进行深度的更新操作，这虽然不会改变基本操作的渐进时间复杂度，但会增加常数因子的时间开销。

以下是更新节点深度的一种可能的方法：

type Node struct {
    // 其他已有属性...
    Depth int
    // ...
}

func updateDepth(node *Node, depth int) {
    node.Depth = depth
    if node.Left != nil {
        updateDepth(node.Left, depth + 1)
    }
    if node.Right != nil {
        updateDepth(node.Right, depth + 1)
    }
}

// 在插入或旋转等操作后，从根节点开始更新深度
func updateTreeDepth(root *Node) {
    updateDepth(root, 0)
}

再次强调，对于红黑树而言，这不是必须的操作，通常情况下我们会根据需要计算特定节点的深度而非预先存储。

天工：

在Go语言中，红黑树的操作复杂度是O(log n)，这是在红黑树的一些性质保证下的结果，比如：每个节点不是红的就是黑的；从任一节点到其子节点的所有路径都包含相同数量的黑节点等。

如果我们想要在结点中添加一个新的属性，比如黑高，那么我们需要在每次对红黑树进行操作（比如插入、删除、查找）的时候，更新这个新的属性。这可能会增加一些运行时间，但不会影响到红黑树的渐进性能，因为这些更新操作的时间复杂度也是O(log n)。

至于如何维护结点的深度，实际上在每次对红黑树进行操作的时候，我们都需要更新结点的深度。比如在插入新节点的时候，我们需要递归地更新新节点及其父节点的深度；在删除节点的时候，我们也需要递归地更新被删除节点及其父节点的深度。这样，我们就可以在需要的时候获取到任意节点的深度。

灵小智：

在红黑树中，黑高是每个结点到其叶子节点的黑色结点数量。通过将结点的黑高作为结点属性来维护红黑树并不会影响其操作的渐近性能。

在使用Go语言实现红黑树时，可以在结点结构体中添加一个属性来表示该结点的黑高。当进行插入、删除等操作时，需要相应地更新每个结点的黑高。以下是一种可能的方法来实现这一点：

1.在结点结构体中添加一个名为"blackHeight"的属性，用于记录结点的黑高。

2.在进行插入或删除操作时，如果结点发生了旋转或颜色变换，需要更新相关结点的黑高。

• 如果结点的左右孩子其中之一发生了改变，那么新的孩子结点的黑高将等于旧的孩子结点的黑高。如果两个孩子都发生了改变，那么新的左右孩子结点的黑高将相等。

• 如果结点的颜色发生了变化，且结点由红变黑，那么黑高加1；如果结点由黑变红，那么黑高减1。

3.每次更新黑高后，需要递归地向上更新父节点的黑高直到根节点。

通过这种方法，红黑树的渐近性能不会受到影响，并且仍然满足红黑树的所有性质。

关于如何维护结点的深度，红黑树通常不需要显式地维护结点的深度。深度可以通过遍历树的过程中计算得出。例如，可以使用深度优先搜索或广度优先搜索算法来遍历红黑树，并在遍历过程中记录每个结点的深度。

chatgpt：

在红黑树中，黑高是一个重要的性质，它需要保持平衡以确保红黑树的渐进性能。如果我们将结点的黑高作为树中结点的一个属性来维护，并且不改变红黑树的任何操作，这可能会导致无法满足红黑树的平衡条件。

红黑树中的平衡条件包括：

1.每个节点要么是红色，要么是黑色。

2.根节点是黑色。

3.每个叶子节点（NIL 节点）是黑色。

4.如果一个节点是红色的，则它的两个子节点都是黑色。

5.对于每个节点，从该节点到其后代叶子节点的简单路径上，均包含相同数目的黑色节点（即具有相同的黑高）。

如果我们将结点的深度作为附加属性来维护，可以通过遍历整棵树并计算每个结点到根节点之间所经过的边数来实现。然而，在插入、删除等操作时，由于调整和旋转可能改变了结点之间的关系和路径长度，必须对整棵树进行重新计算。这样做会带来额外的开销，并且可能影响原始红黑树操作的渐进性能。

因此，在不影响红黑树任何操作的渐进性能的前提下，将结点的黑高作为树中结点的一个属性来维护是不可行的。维护结点深度同样面临类似的问题。红黑树之所以被广泛使用，是因为它通过保持平衡性质而保证了较好的性能，并且在插入、删除等操作时仅需要进行有限次数的旋转和颜色调整。

kimi：

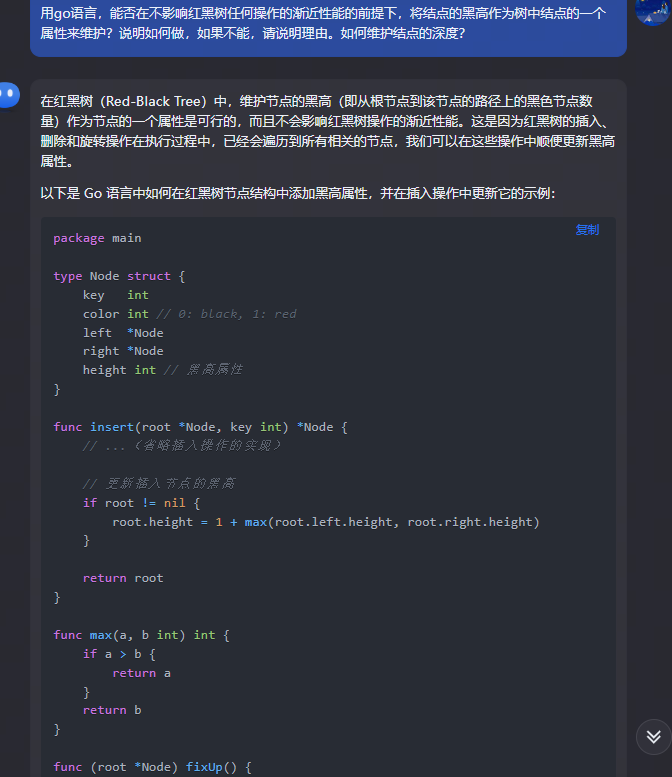
在红黑树（Red-Black Tree）中，维护节点的黑高（即从根节点到该节点的路径上的黑色节点数量）作为节点的一个属性是可行的，而且不会影响红黑树操作的渐近性能。这是因为红黑树的插入、删除和旋转操作在执行过程中，已经会遍历到所有相关的节点，我们可以在这些操作中顺便更新黑高属性。

以下是 Go 语言中如何在红黑树节点结构中添加黑高属性，并在插入操作中更新它的示例：

package main

type Node struct {
    key   int
    color int // 0: black, 1: red
    left  *Node
    right *Node
    height int // 黑高属性
}

func insert(root *Node, key int) *Node {
    // ...（省略插入操作的实现）

    // 更新插入节点的黑高
    if root != nil {
        root.height = 1 + max(root.left.height, root.right.height)
    }

    return root
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

func (root *Node) fixUp() {
    // ...（省略修复红黑树性质的代码）
}

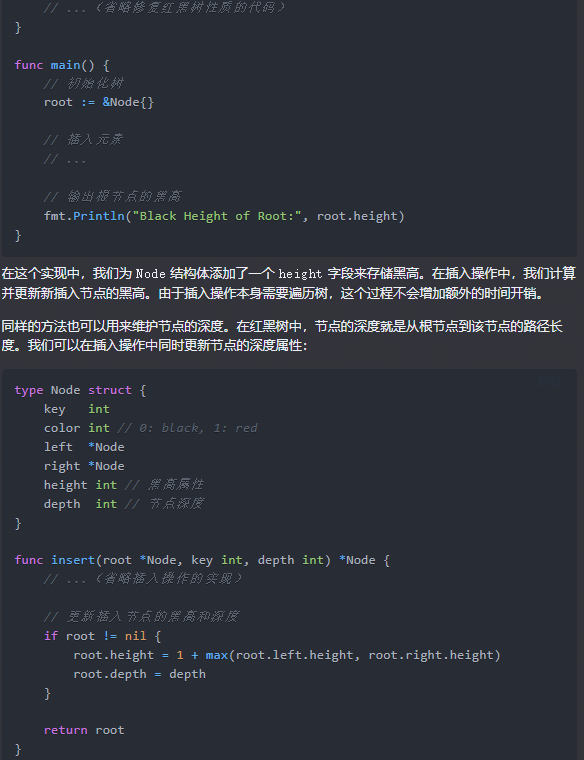
func main() {
    // 初始化树
    root := &Node{}

    // 插入元素
    // ...

    // 输出根节点的黑高
    fmt.Println("Black Height of Root:", root.height)
}

在这个实现中，我们为 Node 结构体添加了一个 height 字段来存储黑高。在插入操作中，我们计算并更新新插入节点的黑高。由于插入操作本身需要遍历树，这个过程不会增加额外的时间开销。

同样的方法也可以用来维护节点的深度。在红黑树中，节点的深度就是从根节点到该节点的路径长度。我们可以在插入操作中同时更新节点的深度属性：

type Node struct {
    key   int
    color int // 0: black, 1: red
    left  *Node
    right *Node
    height int // 黑高属性
    depth  int // 节点深度
}

func insert(root *Node, key int, depth int) *Node {
    // ...（省略插入操作的实现）

    // 更新插入节点的黑高和深度
    if root != nil {
        root.height = 1 + max(root.left.height, root.right.height)
        root.depth = depth
    }

    return root
}

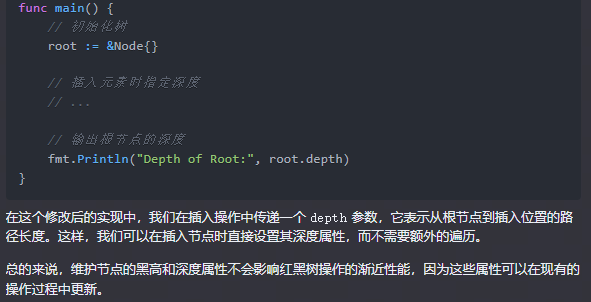
func main() {
    // 初始化树
    root := &Node{}

    // 插入元素时指定深度
    // ...

    // 输出根节点的深度
    fmt.Println("Depth of Root:", root.depth)
}

在这个修改后的实现中，我们在插入操作中传递一个 depth 参数，它表示从根节点到插入位置的路径长度。这样，我们可以在插入节点时直接设置其深度属性，而不需要额外的遍历。

总的来说，维护节点的黑高和深度属性不会影响红黑树操作的渐近性能，因为这些属性可以在现有的操作过程中更新。

混元：

在Go语言中，可以在不影响红黑树任何操作的渐近性能的前提下，将结点的黑高作为树中结点的一个属性来维护。具体实现方法如下：

1. 定义一个新的结点结构体，包含红黑树结点的基本属性（如颜色、左右子结点等）以及黑高属性。例如：

type Node struct {
    Key        int
    Value      interface{}
    Left       *Node
    Right      *Node
    Parent     *Node
    Color      Color
    BlackDepth int // 黑高属性
}

2. 在红黑树的插入、删除等操作中，同步更新结点的黑高属性。具体实现需要对红黑树的操作进行修改，以保证黑高属性的正确性。

3. 在查询黑高时，直接访问结点的黑高属性即可。

这种方法不会影响红黑树的任何操作的渐近性能，因为黑高属性的维护是在红黑树操作的基础上进行的，不会增加额外的时间复杂度。

维护结点的深度可以通过递归的方式实现。对于每个结点，计算其左右子树的深度，然后取较大值加1。具体实现如下：

func (n *Node) Depth() int {
    if n == nil {
        return 0
    }
    leftDepth := n.Left.Depth()
    rightDepth := n.Right.Depth()
    if leftDepth > rightDepth {
        return leftDepth + 1
    } else {
        return rightDepth + 1
    }
}

这样，可以在不影响红黑树任何操作的渐近性能的前提下，将结点的黑高作为树中结点的一个属性来维护，并维护结点的深度。