2024-01-31：用go语言，机器人正在玩一个古老的基于DOS的游戏， 游戏中有N+1座建筑，从0到N编号，从左到右排列， 编号为0的建筑高度为0个单位，编号为i的建筑的高度为H(i)个单位， 起
2024-01-31：用go语言，机器人正在玩一个古老的基于DOS的游戏，
游戏中有N+1座建筑，从0到N编号，从左到右排列，
编号为0的建筑高度为0个单位，编号为i的建筑的高度为H(i)个单位，
起初， 机器人在编号为0的建筑处，
每一步，它跳到下一个（右边）建筑。假设机器人在第k个建筑，且它现在的能量值是E，
下一步它将跳到第个k+1建筑，
它将会得到或者失去正比于与H(k+1)与E之差的能量，
如果 H(k+1) > E 那么机器人就失去H(k+1)-E的能量值，否则它将得到E-H(k+1)的能量值，
游戏目标是到达第个N建筑，在这个过程中，能量值不能为负数个单位。
现在的问题是机器人以多少能量值开始游戏，才可以保证成功完成游戏。
来自字节。
答案2024-01-31：
来自左程云。
大体步骤如下：
1.首先，根据给定的输入数组inputs，初始化变量n为第一个元素的值（即建筑数量）。
2.初始化变量l（左边界）、r（右边界）、max（最大高度）为0。
3.通过循环遍历n次，将inputs中的建筑高度依次存储到数组arr中，并更新r为当前最大高度。
4.初始化变量m为0，ans为-1。这两个变量将用于记录二分搜索的结果。
5.进行二分搜索，当左边界l小于等于右边界r时，执行以下步骤：
5.1.计算中间值m为(l + r) / 2。
5.2.调用函数ok(m, max)判断以m为能量值是否能完成游戏：
5.2.1.在循环中，检查当前能量值sum是否非负且不超过最大高度max，并遍历建筑。
5.2.2.如果sum小于等于当前建筑高度arr[i]，则机器人失去(arr[i] - sum)的能量。
5.2.3.否则，机器人得到(sum - arr[i])的能量。
5.2.4.如果sum仍然非负，则返回true表示以m为能量值可以完成游戏，否则返回false。
5.3.如果ok(m, max)返回true，更新ans为m，并将右边界r更新为m-1。
5.4.否则，将左边界l更新为m+1。
6.输出结果ans，即最低能量值开始游戏可以保证成功完成游戏。
总的时间复杂度：O(n log H)，其中n为建筑数量，H为最大高度。因为进行了一次二分搜索，每次判断所需的时间复杂度为O(n)，而循环内部还需要遍历建筑，总时间复杂度为O(n)。由于最大高度max是在遍历建筑时计算得到的，因此总时间复杂度为O(n log H)。
总的额外空间复杂度：O(N)，其中N为常数，数组arr的大小为MAXN，而MAXN为一个较大的常数。
go完整代码如下：
package main
import (
"fmt"
)
const MAXN = 100001
var arr [MAXN]int
var n int
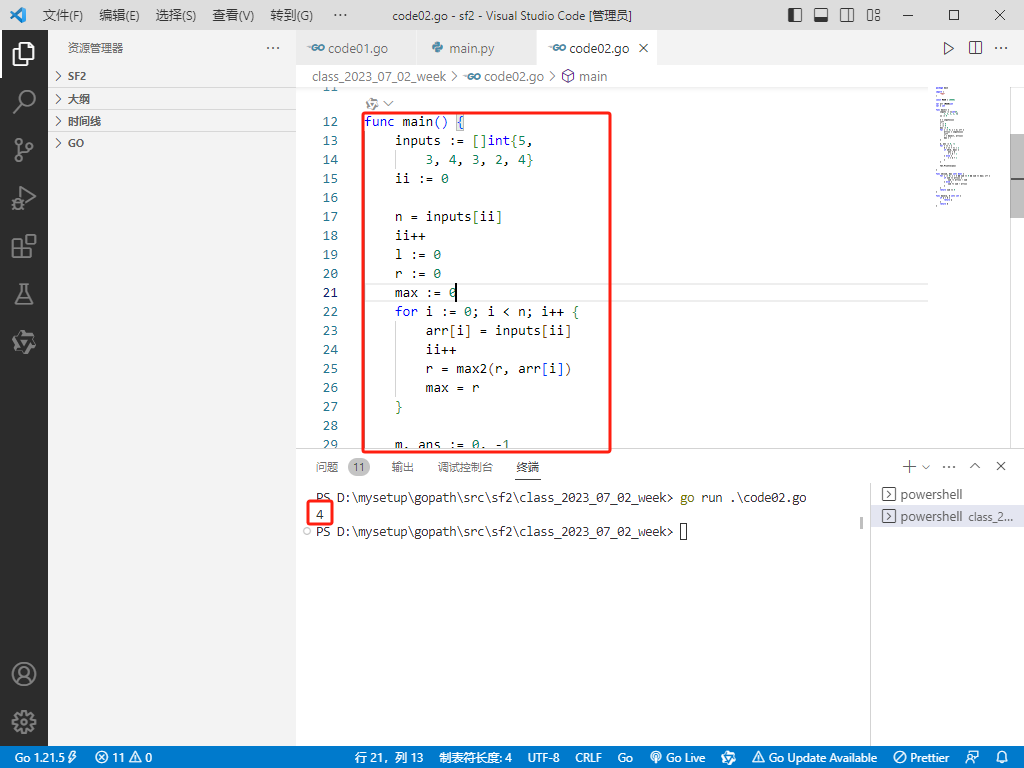
func main() {
inputs := []int{5,
3, 4, 3, 2, 4}
ii := 0
n = inputs[ii]
ii++
l := 0
r := 0
max := 0
for i := 0; i < n; i++ {
arr[i] = inputs[ii]
ii++
r = max2(r, arr[i])
max = r
}
m, ans := 0, -1
for l <= r {
m = (l + r) / 2
if ok(m, max) {
ans = m
r = m - 1
} else {
l = m + 1
}
}
fmt.Println(ans)
}
func ok(sum, max int) bool {
for i := 0; i < n && sum >= 0 && sum <= max; i++ {
if sum <= arr[i] {
sum -= arr[i] - sum
} else {
sum += sum - arr[i]
}
}
return sum >= 0
}
func max2(a, b int) int {
if a > b {
return a
}
return b
}
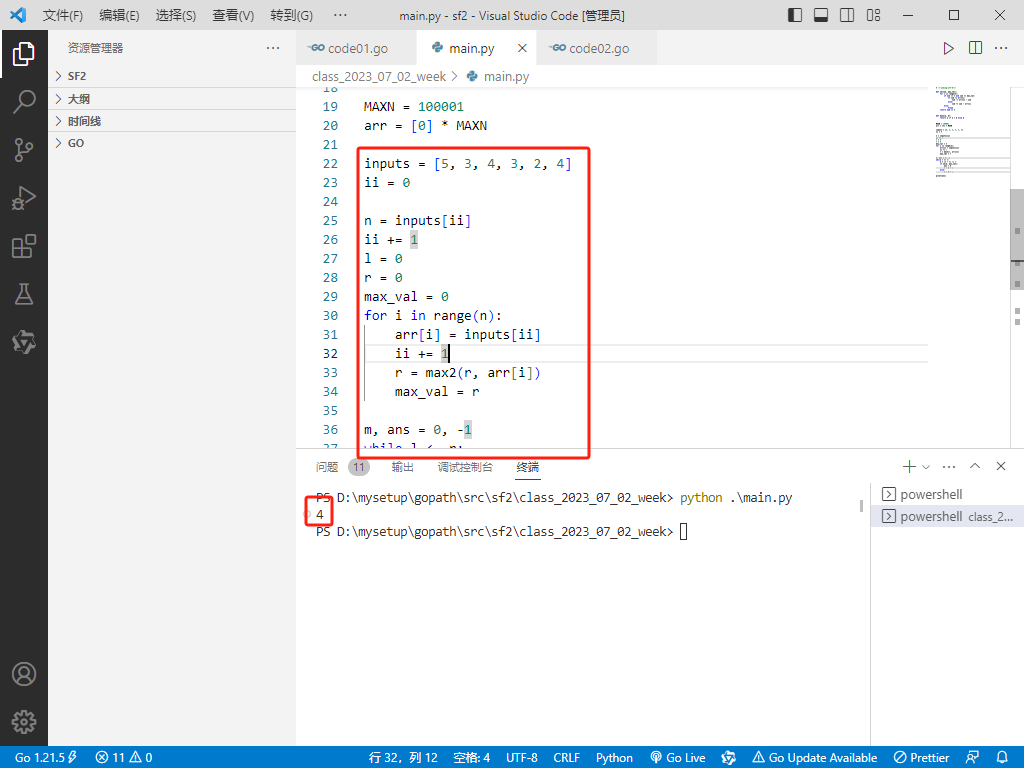
python完整代码如下：
# -*-coding:utf-8-*-
def ok(sum, max_val):
for i in range(n):
if sum >= 0 and sum <= max_val:
if sum <= arr[i]:
sum -= arr[i] - sum
else:
sum += sum - arr[i]
else:
break
return sum >= 0
def max2(a, b):
return a if a > b else b
MAXN = 100001
arr = [0] * MAXN
inputs = [5, 3, 4, 3, 2, 4]
ii = 0
n = inputs[ii]
ii += 1
l = 0
r = 0
max_val = 0
for i in range(n):
arr[i] = inputs[ii]
ii += 1
r = max2(r, arr[i])
max_val = r
m, ans = 0, -1
while l <= r:
m = (l + r) // 2
if ok(m, max_val):
ans = m
r = m - 1
else:
l = m + 1
print(ans)
