文心一言 VS 讯飞星火 VS chatgpt （189）-- 算法导论14.1 6题

六、用go语言，在OS-SELECT或OS-RANK中，注意到无论什么时候引用结点的size属性都是为了计算一个秩。相应地，假设每个结点都存储它在以自己为根的子树中的秩。试说明在插入和删除时，如何维护这个信息。(注意，这两种操作都可能引起旋转。)

文心一言：

在OS-SELECT和OS-RANK中，我们维护一个树形结构，其中每个节点都有一个size属性，该属性表示该节点及其所有子孙节点中的元素数量。在OS-SELECT中，我们经常需要访问一个节点的size属性，以确定该节点的秩（rank）。

在插入和删除操作中，我们可能需要进行旋转操作来保持树的平衡。旋转操作包括左旋（left rotation）和右旋（right rotation）。在旋转操作之后，我们需要更新节点的size属性，以及其所有祖先节点的size属性。

以下是在插入和删除操作中如何维护size属性的基本步骤：

插入操作：

找到插入位置的前驱节点predecessor和后继节点successor。
将新元素插入到正确的位置。
更新predecessor和successor的size属性。
如果插入导致树不平衡，需要进行旋转操作。在旋转之后，需要更新所有受影响的节点的size属性。
删除操作：

找到要删除的元素。
删除该元素。
更新受影响的节点的size属性。
如果删除导致树不平衡，需要进行旋转操作。在旋转之后，需要更新所有受影响的节点的size属性。
具体来说，对于每个节点node，它的size属性可以通过以下方式计算：

如果node是一个叶子节点（没有子节点），那么它的size属性就是1。
否则，它的size属性是其左子树中所有节点的size属性的总和加上其右子树中所有节点的size属性的总和再加上1（加上1是因为要包括node本身）。
在旋转操作之后，我们需要递归地更新所有受影响的节点的size属性。例如，在左旋之后，原来的root节点变成了其右子树的根节点，我们只需要递归地更新这个新的root节点以及其左子树的size属性即可。

通过这种方式，我们可以在O(log n)的时间内插入、删除元素并维护每个节点的size属性，从而可以在O(log n)的时间内进行OS-SELECT和OS-RANK操作。

讯飞星火：

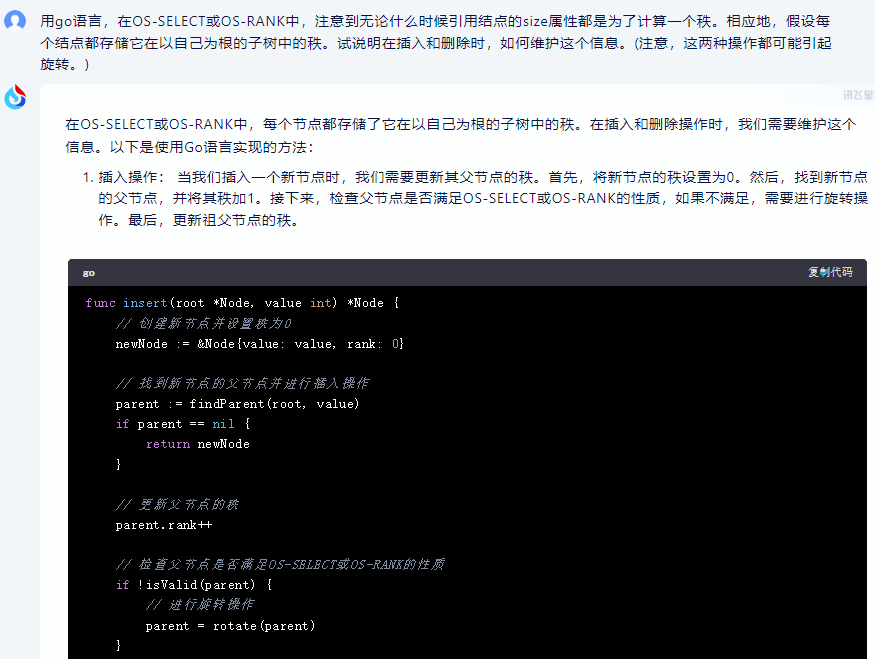
在OS-SELECT或OS-RANK中，每个节点都存储了它在以自己为根的子树中的秩。在插入和删除操作时，我们需要维护这个信息。以下是使用Go语言实现的方法：

1. 插入操作：
   当我们插入一个新节点时，我们需要更新其父节点的秩。首先，将新节点的秩设置为0。然后，找到新节点的父节点，并将其秩加1。接下来，检查父节点是否满足OS-SELECT或OS-RANK的性质，如果不满足，需要进行旋转操作。最后，更新祖父节点的秩。

func insert(root *Node, value int) *Node {
    // 创建新节点并设置秩为0
    newNode := &Node{value: value, rank: 0}

    // 找到新节点的父节点并进行插入操作
    parent := findParent(root, value)
    if parent == nil {
        return newNode
    }

    // 更新父节点的秩
    parent.rank++

    // 检查父节点是否满足OS-SELECT或OS-RANK的性质
    if !isValid(parent) {
        // 进行旋转操作
        parent = rotate(parent)
    }

    // 更新祖父节点的秩
    grandParent := findGrandParent(root, parent)
    if grandParent != nil {
        grandParent.rank++
    }

    return root
}

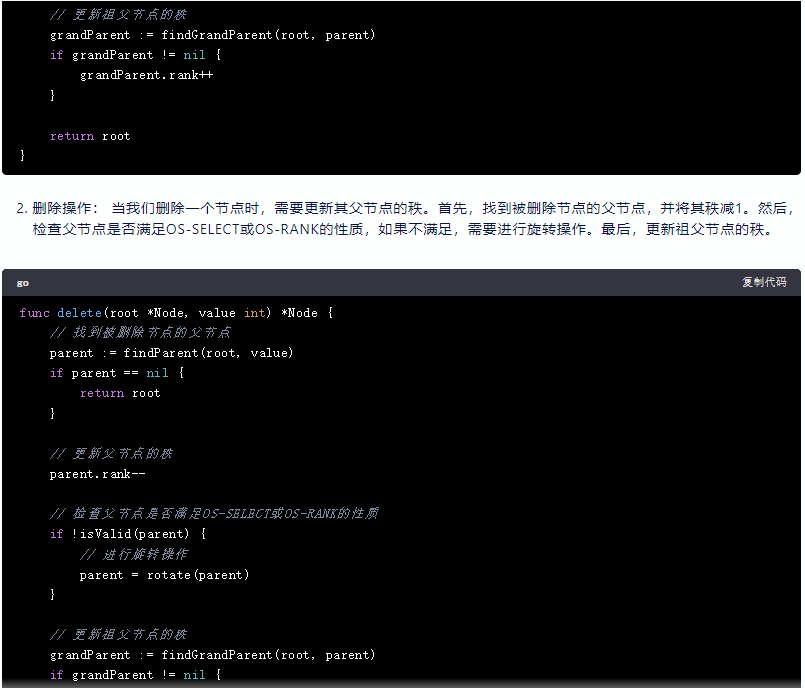
2. 删除操作：
   当我们删除一个节点时，需要更新其父节点的秩。首先，找到被删除节点的父节点，并将其秩减1。然后，检查父节点是否满足OS-SELECT或OS-RANK的性质，如果不满足，需要进行旋转操作。最后，更新祖父节点的秩。

func delete(root *Node, value int) *Node {
    // 找到被删除节点的父节点
    parent := findParent(root, value)
    if parent == nil {
        return root
    }

    // 更新父节点的秩
    parent.rank--

    // 检查父节点是否满足OS-SELECT或OS-RANK的性质
    if !isValid(parent) {
        // 进行旋转操作
        parent = rotate(parent)
    }

    // 更新祖父节点的秩
    grandParent := findGrandParent(root, parent)
    if grandParent != nil {
        grandParent.rank--
    }

    return root
}

注意：这里的代码仅作为示例，实际实现可能需要根据具体的数据结构和旋转操作进行调整。

360智脑：

在Go语言中，为了在OS-SELECT或OS-RANK中维护节点的大小属性，可以采用以下方法：

1. 在插入操作中：

   • 首先，按照常规方法进行插入操作，然后根据新插入节点的大小更新其父节点的大小属性。如果插入操作引起了旋转，需要更新旋转后新父节点的大小属性。
   • 在更新过程中，如果节点的左子树大小加1，则该节点的大小加1；如果节点的右子树大小加1，则该节点的大小减1。这样可以保证节点的大小属性始终反映其在以自己为根的子树中的秩。

2. 在删除操作中：

   • 首先，按照常规方法进行删除操作，然后根据删除节点的大小更新其父节点的大小属性。如果删除操作引起了旋转，需要更新旋转后新父节点的大小属性。
   • 在更新过程中，如果删除的节点是左子节点，其父节点的左子树大小减1；如果删除的节点是右子节点，其父节点的右子树大小减1。这样可以保证节点的大小属性始终反映其在以自己为根的子树中的秩。

通过以上方法，在插入和删除操作中可以有效地维护节点的大小属性，从而实现OS-SELECT或OS-RANK中的秩计算。

智谱清言：

在Go语言中，维护一个以自己为根的子树中的秩属性，在二叉树中通常指的是维护每个节点的左子树和右子树的高度或深度。这样的树结构常被用于实现诸如优先队列（通过二叉堆实现）等数据结构。在这种数据结构中，节点的秩是其在树中的深度，根节点为深度0。

对于插入和删除操作，我们需要确保维护节点秩的正确性，因为这些操作可能会改变树的结构，从而影响节点的秩。旋转是维护树平衡的一种操作，它可以在插入或删除节点后执行，以保证树的高度最小。

下面是如何在插入和删除时维护节点秩的说明：

插入操作

1.插入节点：首先按照二叉搜索树的规则插入新节点。

2.更新父节点秩：如果新插入的节点不是根节点，那么它的父节点的秩需要增加1，因为子树的高度增加了。

3.更新祖父节点秩：如果新插入的节点不是根节点的直接子节点，那么它的祖父节点的秩也需要增加1。

4.检查并调整平衡：插入节点后，可能需要通过旋转来维持树的平衡。这通常涉及到修复因插入而可能失衡的树。

删除操作

1.删除节点：首先找到要删除的节点，并从树中移除它。

2.更新子树秩：删除的节点如果有子节点，那么它原来的子树的高度需要重新计算。

3.更新兄弟节点秩：如果被删除的节点是其父节点的一个子节点，那么其父节点的另一个子节点的秩可能需要调整。

4.更新父节点秩：如果被删除的节点是父节点的一个子节点，那么父节点的秩可能需要调整。

5.检查并调整平衡：删除节点后，同样可能需要通过旋转来维持树的平衡。

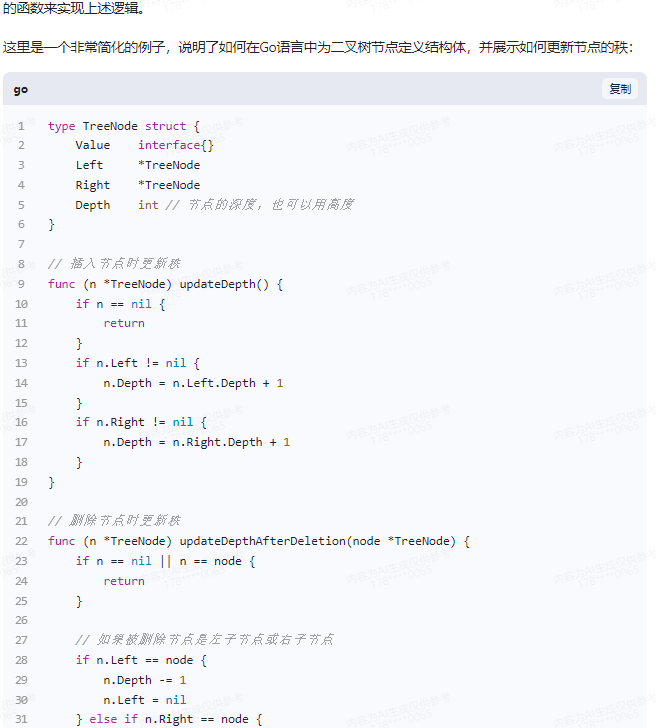
在Go语言中，可以通过定义一个树结构，其中每个节点包含其左右子树的深度，以及相应的更新和调整平衡的函数来实现上述逻辑。

这里是一个非常简化的例子，说明了如何在Go语言中为二叉树节点定义结构体，并展示如何更新节点的秩：

type TreeNode struct {
    Value    interface{}
    Left     *TreeNode
    Right    *TreeNode
    Depth    int // 节点的深度，也可以用高度
}
// 插入节点时更新秩
func (n *TreeNode) updateDepth() {
    if n == nil {
        return
    }
    if n.Left != nil {
        n.Depth = n.Left.Depth + 1
    }
    if n.Right != nil {
        n.Depth = n.Right.Depth + 1
    }
}
// 删除节点时更新秩
func (n *TreeNode) updateDepthAfterDeletion(node *TreeNode) {
    if n == nil || n == node {
        return
    }
    // 如果被删除节点是左子节点或右子节点
    if n.Left == node {
        n.Depth -= 1
        n.Left = nil
    } else if n.Right == node {
        n.Depth -= 1
        n.Right = nil
    }
    // 递归更新其他子节点
    n.updateDepth()
}

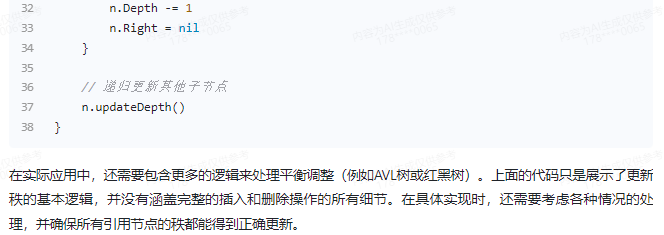
在实际应用中，还需要包含更多的逻辑来处理平衡调整（例如AVL树或红黑树）。上面的代码只是展示了更新秩的基本逻辑，并没有涵盖完整的插入和删除操作的所有细节。在具体实现时，还需要考虑各种情况的处理，并确保所有引用节点的秩都能得到正确更新。

通义千问：

在AVL树或红黑树等自平衡二叉搜索树中，为了支持快速的排名查询（如OS-SELECT和OS-RANK操作），可以为每个节点存储一个额外的属性size，表示以该节点为根的子树中的节点总数。这样，在查询时无需实际遍历子树即可直接获取秩信息。

对于插入和删除操作，维护这个size属性需要随着树结构的变化同步更新：

1. 插入操作：

   • 新插入一个节点时，它的初始size为1。
   • 在向上回溯调整平衡因子的过程中，沿途经过的所有祖先节点的size都需要增加1，因为它们各自子树的大小都增加了1个节点。
   • 如果发生旋转操作（左旋或右旋），旋转后涉及的父节点、旋转节点及其子节点的size都需要重新计算：
     • 被旋转节点的size是其两个子节点size之和。
     • 旋转节点的新父节点（可能是原父节点或原兄弟节点）的size也需要相应更新为其左右子节点size之和。

2. 删除操作：

   • 删除一个节点时，首先将该节点的size从其父节点的size中减去。
   • 同样在向上回溯调整平衡因子的过程中，沿途经过的所有祖先节点的size都需要减少1，因为它们各自子树的大小减少了1个节点。
   • 如果进行旋转操作来恢复平衡：
     • 旋转后的各相关节点的size同样需要重新计算，确保正确反映新的子树大小。

具体到Go语言实现时，可以在节点结构体中定义一个size字段，并在插入和删除方法中包含相应的更新逻辑。例如，在执行插入或删除操作之后，递归地更新当前节点及其祖先节点的size属性，直到达到根节点为止。如果涉及到旋转操作，则在旋转函数内部处理size属性的更新。

天工：

在Go语言中，可以通过在节点类型中添加一个属性来存储每个节点的秩信息。例如：

type Node struct {
    Element int
    Size    int
    Left    *Node
    Right   *Node
}

在插入和删除节点时，我们需要更新相关节点的秩信息。具体来说：

1. 在插入新节点时，首先将其初始大小设置为1（因为新节点只包含一个元素），然后递归下降到树中，遇到比新节点大的节点时向右转，遇到比新节点小的节点时向左转，并在转动的节点上更新其子树的大小。

2. 在删除节点时，首先递归下降到树中，找到要删除的节点，然后根据其子树的大小来选择要删除的子节点，并在删除子节点时更新其父节点的大小信息。

需要注意的是，在旋转操作时，需要更新旋转节点的大小信息。例如，在右旋操作中，旋转节点的大小需要加上其右子树的大小；在左旋操作中，旋转节点的大小需要加上其左子树的大小。这样，就可以在插入和删除操作中正确地维护节点的秩信息了。

灵小智：

在使用go语言实现OS-SELECT或OS-RANK算法时，为了维护节点的size属性和秩信息，我们需要在每个节点上添加一个额外的字段来存储秩。这个字段可以是一个整数，表示以该节点为根的子树的大小。

对于插入操作，首先进行二叉搜索树的插入过程，找到合适的位置将新节点插入。在插入节点的过程中，我们需要更新每个经过的节点的size属性，将其增加1。具体步骤如下：

1. 从根节点开始，沿着正确的路径向下遍历，直到找到插入位置。
2. 在遍历过程中，对经过的每个节点，将其size属性增加1。
3. 插入新节点到正确的位置。

在删除操作中，同样需要进行二叉搜索树的删除过程，并且在删除节点后，需要更新每个经过节点的size属性，将其减去被删除节点的大小。具体步骤如下：

1. 找到要删除的节点，并记录其size属性值。
2. 根据删除节点的情况，进行相应的删除操作（可能需要进行旋转操作）。
3. 在删除节点后，从删除节点的父节点开始向上遍历，更新每个经过的节点的size属性，将其减去被删除节点的大小。

这样，通过在每个节点上维护size属性，我们可以始终保持节点在以自己为根的子树中的秩的正确性。无论是插入还是删除操作，都能够正确地更新和维护这个信息。

chatgpt：

在使用Go语言实现OS-SELECT和OS-RANK算法时，可以通过以下方式来维护结点的size属性和秩信息：

1. 插入操作：

   • 首先执行正常的二叉搜索树插入操作。
   • 在向下递归插入过程中，更新每个经过的结点的size属性，将其增加1。
   • 完成插入后，回溯到根节点并对旋转进行调整。在回溯过程中，更新每个经过的结点的size属性。

2. 删除操作：

   • 首先执行正常的二叉搜索树删除操作。
   • 在向下递归删除过程中，更新每个经过的结点的size属性，将其减去1。
   • 完成删除后，回溯到根节点并对旋转进行调整。在回溯过程中，更新每个经过的结点的size属性。

注意：由于插入和删除操作可能引起旋转，在调整树结构时需要确保同时更新父节点、左子节点和右子节点之间正确的size值。此外，在进行旋转时还需要考虑平衡因子等其他相关信息以确保维持平衡。

以上是一种基本思路来维护结点大小和秩信息，在具体实现中还需考虑具体数据结构设计、指针操作等细节。

kimi：

在顺序统计树（Order Statistic Tree）中，维护每个节点的 size 属性（即以该节点为根的子树中的节点数量）对于执行 OS-SELECT 和 OS-RANK 操作至关重要。在插入和删除操作中，我们需要更新这些属性以保持信息的准确性。以下是在 Go 语言中维护 size 属性的策略：

1. 插入操作：

   • 当新节点被插入时，我们需要更新其父节点、祖父节点以及所有祖先节点的 size 属性。这可以通过递归向上更新实现。
   • 如果插入操作导致旋转，旋转后的节点（无论是左旋还是右旋）的 size 属性需要重新计算，因为旋转可能会改变子树的结构。

2. 删除操作：

   • 当节点被删除时，我们需要更新其父节点的 size 属性，因为子树的节点数量减少了。
   • 如果删除操作导致旋转，旋转后的节点的 size 属性同样需要更新。

以下是一个简化的 Go 语言代码示例，展示了如何在插入和删除操作中维护 size 属性：

package main

type Node struct {
    key   int
    size  int // 子树中的节点数量
    left  *Node
    right *Node
}

func insert(root *Node, key int) *Node {
    if root == nil {
        return &Node{key: key, size: 1}
    }

    if key < root.key {
        root.left = insert(root.left, key)
        root.size = 1 + root.left.size + root.right.size
    } else {
        root.right = insert(root.right, key)
        root.size = root.left.size + 1 + root.right.size
    }

    // 如果需要旋转，这里进行旋转操作，并更新旋转后的节点的 size

    return root
}

func delete(root *Node, key int) *Node {
    // ...（省略删除操作的实现）

    // 更新父节点的 size
    if root.parent != nil {
        root.parent.size = 1 + countNodes(root.parent.left) + countNodes(root.parent.right)
    }

    // 如果需要旋转，这里进行旋转操作，并更新旋转后的节点的 size

    return root
}

func countNodes(node *Node) int {
    if node == nil {
        return 0
    }
    return 1 + countNodes(node.left) + countNodes(node.right)
}

func main() {
    // ...（省略树的构建代码）

    // 插入和删除操作
    // ...
}

在这个示例中，我们假设每个节点都有一个指向其父节点的指针 parent。在插入和删除操作中，我们递归地更新 size 属性。如果需要旋转，我们需要在旋转操作后重新计算旋转节点的 size。

请注意，这个代码示例仅提供了一个框架，并没有实现具体的旋转操作。在实际的顺序统计树实现中，你需要根据具体的旋转逻辑来更新 size 属性。

混元：

在 OS-SELECT 和 OS-RANK 中，我们需要维护每个结点的秩，以便在插入和删除操作时快速更新秩。以下是在插入和删除操作中维护结点秩的方法：

1. 插入操作：

在插入操作中，我们首先找到要插入的位置。然后，我们需要更新插入位置的父结点的秩。具体来说，我们需要将插入位置的父结点的秩加 1，因为插入的新结点将增加子树的大小。接下来，我们需要更新插入位置的祖先结点的秩，直到根结点。这是因为插入新结点会影响到插入位置的祖先结点的秩。

2. 删除操作：

在删除操作中，我们首先找到要删除的结点。然后，我们需要更新要删除的结点的父结点的秩。具体来说，我们需要将要删除的结点的父结点的秩减 1，因为删除结点会减少子树的大小。接下来，我们需要更新要删除的结点的祖先结点的秩，直到根结点。这是因为删除结点会影响到要删除的结点的祖先结点的秩。

在插入和删除操作中，如果需要进行旋转，我们需要确保在旋转后更新相关结点的秩。例如，在 AVL 树中，我们可以在旋转后更新旋转的结点和它的父结点的秩。在红黑树中，我们可以在旋转后更新旋转的结点和它的父结点的秩。

总之，在插入和删除操作中，我们需要维护每个结点的秩，以便在操作后快速更新秩。在插入和删除操作中，如果需要进行旋转，我们需要确保在旋转后更新相关结点的秩。这样，我们可以确保在 OS-SELECT 和 OS-RANK 中快速计算秩。