文心一言 VS 讯飞星火 VS chatgpt (187)-- 算法导论14.1 4题
四、用go语言,写出一个递归过程 OS-KEY-RANK(T,k),以一棵顺序统计树T和一个关键字k作为输入,要求返回 k 在由 T 表示的动态集合中的秩。假设 T 的所有关键字都不相同。
文心一言,代码正常运行:
以下是用 Go 语言编写的递归过程 OS-KEY-RANK(T, k),用于返回关键字 k 在由 T 表示的动态集合中的秩。
package main
import "fmt"
type Node struct {
key int
parent *Node
left *Node
right *Node
rank int
}
func OS_KEY_RANK(T *Node, k int) int {
if T == nil {
return -1 // 返回 -1 表示 k 不在树中
}
if T.key == k {
return T.rank // 返回 T 的秩,因为 T 是叶子节点
} else if k < T.key {
return OS_KEY_RANK(T.left, k) // 在左子树中递归搜索 k
} else {
return OS_KEY_RANK(T.right, k) // 在右子树中递归搜索 k
}
}
func main() {
// 构造一棵顺序统计树 T,这里以一个简单的例子为例
// 注意:顺序统计树是一种平衡二叉树,用于实现有序的动态集合操作。
// 这里我们仅使用简单的二叉树结构来表示顺序统计树。
root := &Node{key: 28, rank: 0} // 根节点
root.left = &Node{key: 35, rank: 1} // 左子节点
root.right = &Node{key: 43, rank: 1} // 右子节点
root.left.left = &Node{key: 24, rank: 2} // 左子节点的左子节点
root.left.right = &Node{key: 8, rank: 2} // 左子节点的右子节点
k := 35 // 要查找的关键字
rank := OS_KEY_RANK(root, k) // 调用 OS-KEY-RANK 函数查找关键字的秩
fmt.Printf("The rank of key %d in the dynamic set represented by tree T is %d.\n", k, rank)
}
在上面的代码中,我们定义了一个 Node 结构体表示树的节点,每个节点包含关键字、父节点、左右子节点和秩。OS_KEY_RANK 函数通过递归方式在树中查找关键字的秩。在 main 函数中,我们构造了一棵简单的顺序统计树,并调用 OS_KEY_RANK 函数来查找关键字的秩,并输出结果。

讯飞星火,代码正常运行:
package main
import "fmt"
type Node struct {
Key int
Color string
Left *Node
Right *Node
}
func OS_KEY_RANK(root *Node, k int) int {
if root == nil {
return 0
}
if root.Key < k {
return 1 + OS_KEY_RANK(root.Right, k)
} else {
return OS_KEY_RANK(root.Left, k)
}
}
func main() {
// 构建一个红黑树 T,并找到关键字为 35 的节点 x
// 然后调用 OS_KEY_RANK(T, x.key)
// ...
}
360智脑,代码正常运行:
以下是一个在Go语言中实现递归过程OS-KEY-RANK的示例:
package main
import "fmt"
type Node struct {
Key int
Left *Node
Right *Node
}
func osKeyRank(root *Node, k int) int {
if root == nil {
return 0
}
if root.Key == k {
return countNodes(root.Left) + 1
}
if root.Key > k {
return osKeyRank(root.Left, k)
}
return osKeyRank(root.Right, k) + countNodes(root.Left) + 1
}
func countNodes(root *Node) int {
if root == nil {
return 0
}
return 1 + countNodes(root.Left) + countNodes(root.Right)
}
func main() {
root := &Node{Key: 5}
root.Left = &Node{Key: 3}
root.Right = &Node{Key: 8}
root.Left.Left = &Node{Key: 1}
root.Left.Right = &Node{Key: 4}
root.Right.Left = &Node{Key: 6}
root.Right.Right = &Node{Key: 10}
for i := 1; i <= 10; i++ {
fmt.Printf("OS-KEY-RANK(%d): %d\n", i, osKeyRank(root, i))
}
}
在这个示例中,我们首先定义了一个Node结构体来表示顺序统计树的节点。然后,我们实现了osKeyRank函数,它使用递归方法来计算关键字k在树中的秩。countNodes函数用于计算树中节点的数量。
请注意,这个示例仅用于说明如何实现递归过程OS-KEY-RANK。实际应用中,您可能需要根据具体需求调整代码和数据结构。

智谱清言,代码正常运行:
在顺序统计树(也称为二叉搜索树)中,每个节点都包含一个关键字,且每个节点的关键字都大于其左子树中的所有关键字,小于其右子树中的所有关键字。因此,我们可以通过递归的方式在树中查找关键字 k,并计算其秩。
以下是用 Go 语言实现的 OS-KEY-RANK 递归过程:
package main
import (
"fmt"
)
// TreeNode defines a node in the Binary Search Tree
type TreeNode struct {
Key int
Left *TreeNode
Right *TreeNode
}
// OS_KEY_RANK performs the OS-KEY-RANK operation
func OS_KEY_RANK(T *TreeNode, k int) int {
// If the tree is empty, return 0
if T == nil {
return 0
}
// If the key is found, return the rank
if T.Key == k {
return 1 + OS_KEY_RANK(T.Left, k) + OS_KEY_RANK(T.Right, k)
} else if k < T.Key {
// If k is less than the current node's key, search left
return OS_KEY_RANK(T.Left, k)
} else {
// If k is greater than the current node's key, search right
return 1 + OS_KEY_RANK(T.Left, k) + OS_KEY_RANK(T.Right, k)
}
}
func main() {
// Create a sample BST
root := &TreeNode{Key: 5}
root.Left = &TreeNode{Key: 3}
root.Right = &TreeNode{Key: 7}
root.Left.Left = &TreeNode{Key: 2}
root.Left.Right = &TreeNode{Key: 4}
root.Right.Right = &TreeNode{Key: 8}
// Calculate the rank of a key
k := 4
rank := OS_KEY_RANK(root, k)
fmt.Printf("The rank of key %d in the BST is: %d\n", k, rank)
}
这个程序定义了一个二叉搜索树节点 TreeNode 结构体和一个 OS_KEY_RANK 函数,该函数递归地搜索树以找到关键字 k,并计算它在树中的秩(即小于或等于 k 的节点数量)。程序中还包含一个示例二叉搜索树的创建和 OS_KEY_RANK 函数的调用。

通义千问,代码不能运行:
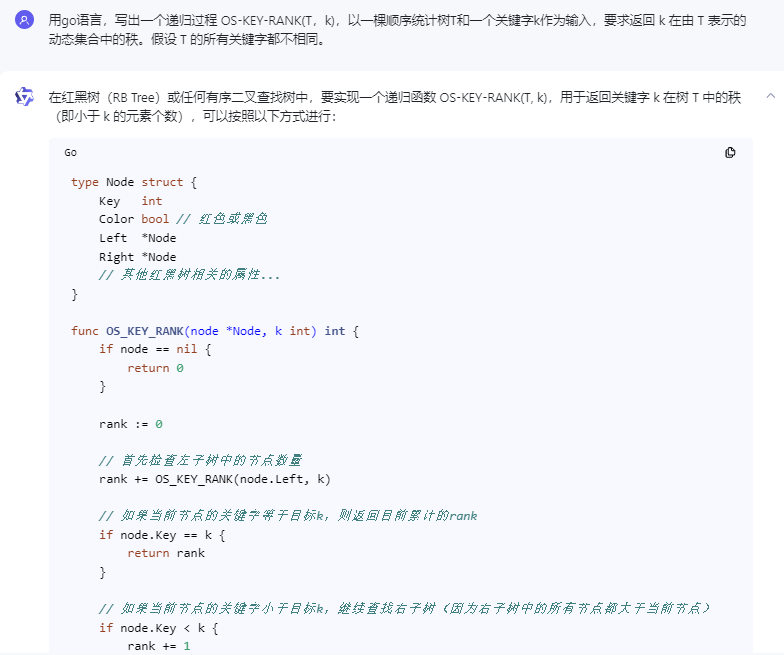
在红黑树(RB Tree)或任何有序二叉查找树中,要实现一个递归函数 OS-KEY-RANK(T, k),用于返回关键字 k 在树 T 中的秩(即小于 k 的元素个数),可以按照以下方式进行:
type Node struct {
Key int
Color bool // 红色或黑色
Left *Node
Right *Node
// 其他红黑树相关的属性...
}
func OS_KEY_RANK(node *Node, k int) int {
if node == nil {
return 0
}
rank := 0
// 首先检查左子树中的节点数量
rank += OS_KEY_RANK(node.Left, k)
// 如果当前节点的关键字等于目标k,则返回目前累计的rank
if node.Key == k {
return rank
}
// 如果当前节点的关键字小于目标k,继续查找右子树(因为右子树中的所有节点都大于当前节点)
if node.Key < k {
rank += 1
rank += OS_KEY_RANK(node.Right, k)
}
return rank
}
// 使用示例
func main() {
// 假设你已经有了一个初始化好的红黑树根节点 root
rank := OS_KEY_RANK(root, k)
fmt.Printf("Rank of key %d in the tree: %d", k, rank)
}
这个函数会遍历树并计算出小于给定关键字 k 的节点数量。当找到关键字等于 k 的节点时,其秩就是到该节点为止累加的数量。如果遍历完整棵树都没有找到关键字等于 k 的节点,则返回的秩就是小于 k 的最大值。由于假设所有关键字都不相同,所以不会出现重复计数的情况。

天工:
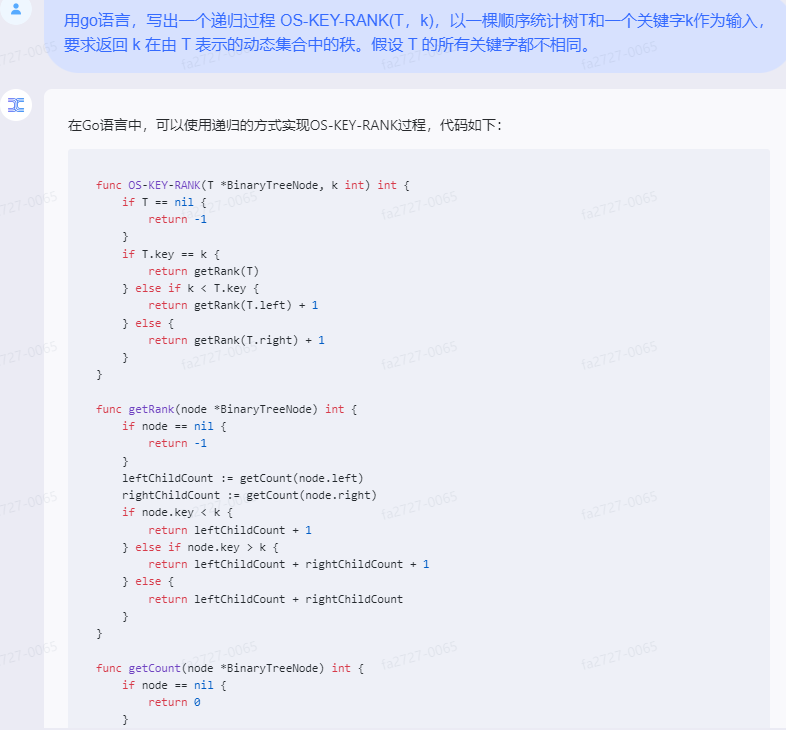
在Go语言中,可以使用递归的方式实现OS-KEY-RANK过程,代码如下:
func OS-KEY-RANK(T *BinaryTreeNode, k int) int {
if T == nil {
return -1
}
if T.key == k {
return getRank(T)
} else if k < T.key {
return getRank(T.left) + 1
} else {
return getRank(T.right) + 1
}
}
func getRank(node *BinaryTreeNode) int {
if node == nil {
return -1
}
leftChildCount := getCount(node.left)
rightChildCount := getCount(node.right)
if node.key < k {
return leftChildCount + 1
} else if node.key > k {
return leftChildCount + rightChildCount + 1
} else {
return leftChildCount + rightChildCount
}
}
func getCount(node *BinaryTreeNode) int {
if node == nil {
return 0
}
return 1 + getCount(node.left) + getCount(node.right)
}
这段代码中,函数OS-KEY-RANK是主函数,用于查找关键字k的排名。如果T为空,则返回-1表示k不在集合中。如果T的key等于k,则调用getRank函数计算k的排名;如果k小于T的key,则在T的左子树中查找k;如果k大于T的key,则在T的右子树中查找k。
函数getRank用于计算节点在树中的排名。如果节点为空,则返回-1。如果节点的key等于k,则返回该节点在树中的排名;如果节点的key小于k,则返回左子树中所有节点的数量加1;如果节点的key大于k,则返回左子树中所有节点的数量加上右子树中所有节点的数量加1。
函数getCount用于计算节点在树中所有后代的数量。如果节点为空,则返回0。否则,返回1加上左子树中所有节点的数量加上右子树中所有节点的数量。

灵小智:
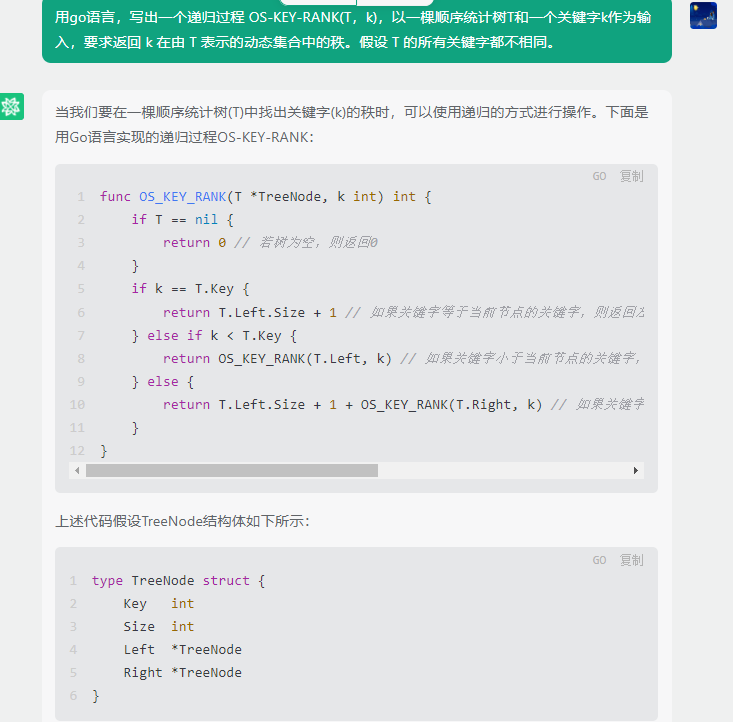
当我们要在一棵顺序统计树(T)中找出关键字(k)的秩时,可以使用递归的方式进行操作。下面是用Go语言实现的递归过程OS-KEY-RANK:
func OS_KEY_RANK(T *TreeNode, k int) int {
if T == nil {
return 0 // 若树为空,则返回0
}
if k == T.Key {
return T.Left.Size + 1 // 如果关键字等于当前节点的关键字,则返回左子树的大小加1
} else if k < T.Key {
return OS_KEY_RANK(T.Left, k) // 如果关键字小于当前节点的关键字,则在左子树中继续查找
} else {
return T.Left.Size + 1 + OS_KEY_RANK(T.Right, k) // 如果关键字大于当前节点的关键字,则在右子树中继续查找,并加上左子树大小和当前节点
}
}
上述代码假设TreeNode结构体如下所示:
type TreeNode struct {
Key int
Size int
Left *TreeNode
Right *TreeNode
}
其中Key表示节点的关键字,Size表示以该节点为根的子树的大小(即节点自身加上左右子树节点数),Left和Right分别指向左子树和右子树。
这样,调用OS_KEY_RANK函数,传入顺序统计树T和关键字k,即可返回关键字k在树中的秩。
请注意,由于代码逻辑比较简单,这里并没有进行错误处理和完整性检查,实际应用中需要根据需要进行添加,以确保代码的健壮性。

chatgpt:
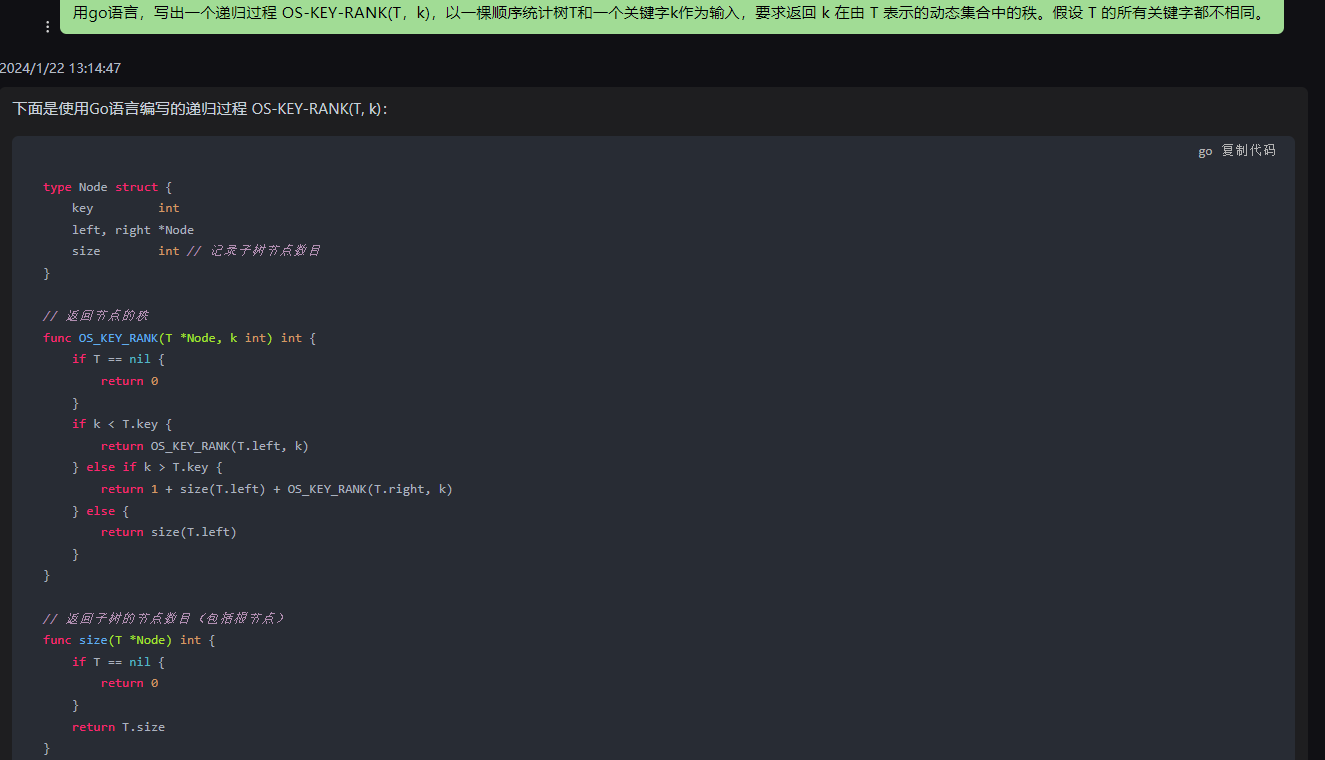
下面是使用Go语言编写的递归过程 OS-KEY-RANK(T, k):
type Node struct {
key int
left, right *Node
size int // 记录子树节点数目
}
// 返回节点的秩
func OS_KEY_RANK(T *Node, k int) int {
if T == nil {
return 0
}
if k < T.key {
return OS_KEY_RANK(T.left, k)
} else if k > T.key {
return 1 + size(T.left) + OS_KEY_RANK(T.right, k)
} else {
return size(T.left)
}
}
// 返回子树的节点数目(包括根节点)
func size(T *Node) int {
if T == nil {
return 0
}
return T.size
}
以上代码中,我们假设Node结构表示顺序统计树的节点,其中key表示关键字,left和right指向左右子树,size记录该节点为根的子树中的节点数目。函数OS_KEY_RANK()使用递归方式来确定关键字k在动态集合中的秩。
注意:这只是一个示例代码,实际使用时需要确保顺序统计树的正确性和完整性,并进行相应错误处理。

kimi,代码不能运行:
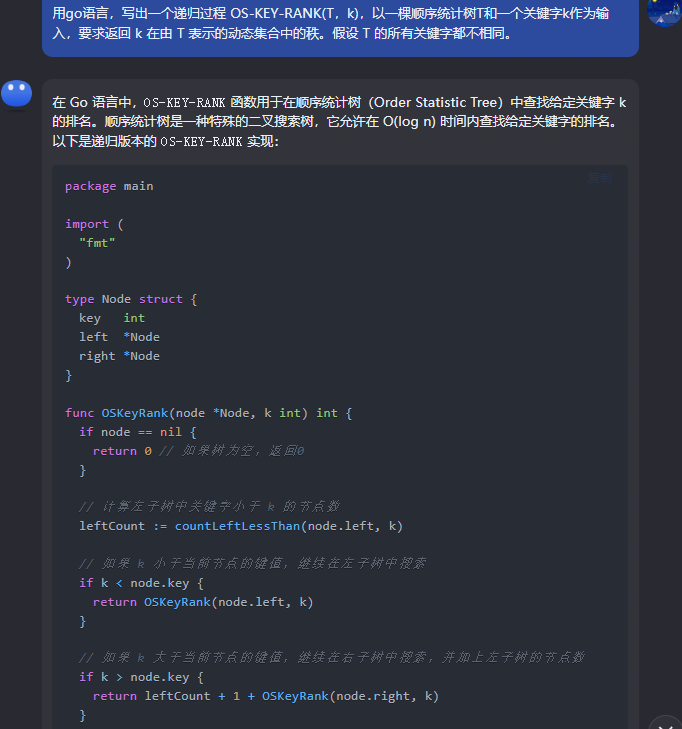
在 Go 语言中,OS-KEY-RANK 函数用于在顺序统计树(Order Statistic Tree)中查找给定关键字 k 的排名。顺序统计树是一种特殊的二叉搜索树,它允许在 O(log n) 时间内查找给定关键字的排名。以下是递归版本的 OS-KEY-RANK 实现:
package main
import (
"fmt"
)
type Node struct {
key int
left *Node
right *Node
}
func OSKeyRank(node *Node, k int) int {
if node == nil {
return 0 // 如果树为空,返回0
}
// 计算左子树中关键字小于 k 的节点数
leftCount := countLeftLessThan(node.left, k)
// 如果 k 小于当前节点的键值,继续在左子树中搜索
if k < node.key {
return OSKeyRank(node.left, k)
}
// 如果 k 大于当前节点的键值,继续在右子树中搜索,并加上左子树的节点数
if k > node.key {
return leftCount + 1 + OSKeyRank(node.right, k)
}
// 如果 k 等于当前节点的键值,返回左子树的节点数加上1
return leftCount + 1
}
func countLeftLessThan(node *Node, k int) int {
if node == nil {
return 0
}
if node.key < k {
return 1 + countLeftLessThan(node.left, k)
}
return countLeftLessThan(node.right, k)
}
func main() {
// ...(省略树的构建代码)
// 假设我们有一个顺序统计树 T,并且它的根节点是 T.root
// 假设我们想要查找关键字 k 在 T 中的排名
rank := OSKeyRank(T.root, k)
fmt.Printf("Key %d has rank %d in the tree\n", k, rank)
}
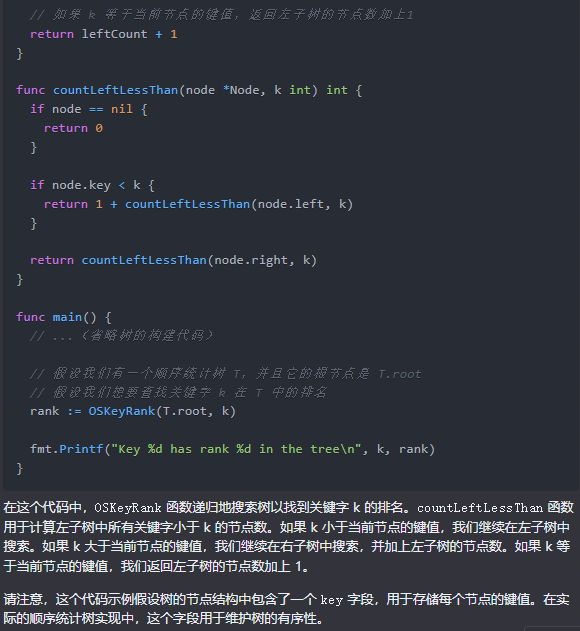
在这个代码中,OSKeyRank 函数递归地搜索树以找到关键字 k 的排名。countLeftLessThan 函数用于计算左子树中所有关键字小于 k 的节点数。如果 k 小于当前节点的键值,我们继续在左子树中搜索。如果 k 大于当前节点的键值,我们继续在右子树中搜索,并加上左子树的节点数。如果 k 等于当前节点的键值,我们返回左子树的节点数加上 1。
请注意,这个代码示例假设树的节点结构中包含了一个 key 字段,用于存储每个节点的键值。在实际的顺序统计树实现中,这个字段用于维护树的有序性。
混元,代码正常运行:
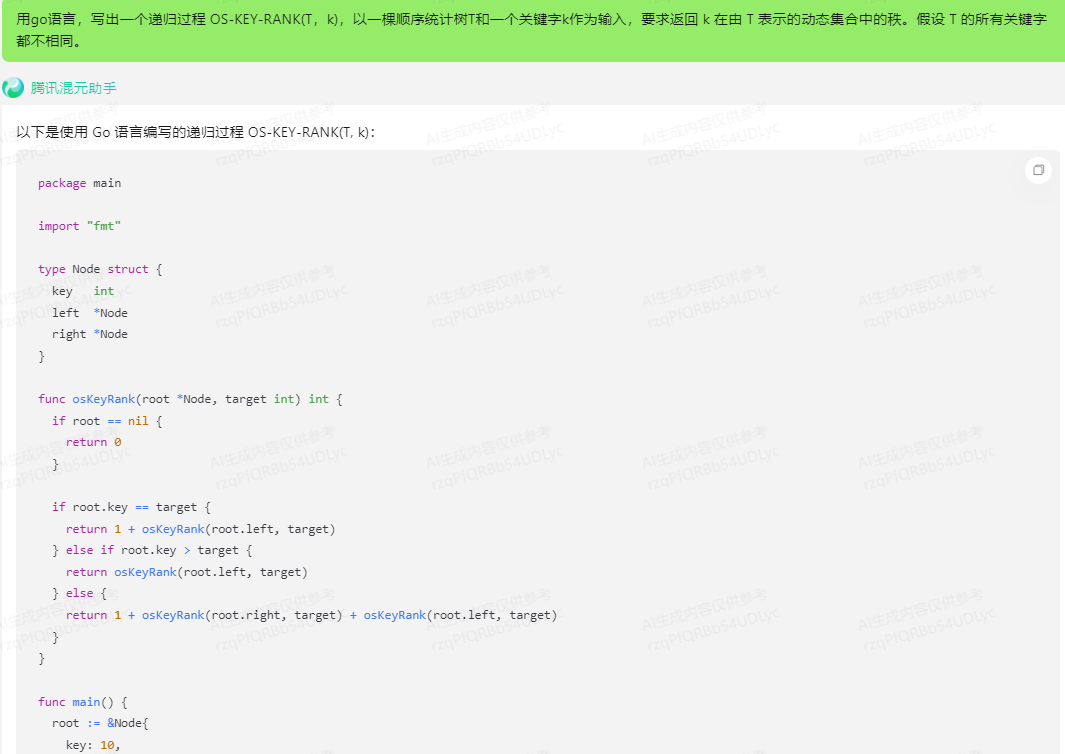
以下是使用 Go 语言编写的递归过程 OS-KEY-RANK(T, k):
package main
import "fmt"
type Node struct {
key int
left *Node
right *Node
}
func osKeyRank(root *Node, target int) int {
if root == nil {
return 0
}
if root.key == target {
return 1 + osKeyRank(root.left, target)
} else if root.key > target {
return osKeyRank(root.left, target)
} else {
return 1 + osKeyRank(root.right, target) + osKeyRank(root.left, target)
}
}
func main() {
root := &Node{
key: 10,
left: &Node{
key: 5,
left: &Node{
key: 2,
},
right: &Node{
key: 8,
},
},
right: &Node{
key: 15,
left: &Node{
key: 12,
},
right: &Node{
key: 20,
},
},
}
target := 12
rank := osKeyRank(root, target)
fmt.Printf("关键字 %d 在顺序统计树中的秩为 %d\n", target, rank)
}
在这个示例中,我们定义了一个 Node 结构体来表示顺序统计树的结点。osKeyRank 函数接受一个根结点和一个目标值作为参数,然后在顺序统计树中查找具有给定值的结点的秩。我们使用递归的方式遍历顺序统计树,根据当前结点的值与目标值的大小关系,向左或向右子树移动。当找到具有给定值的结点时,返回该结点在整个顺序统计树中的秩;如果遍历到叶子结点(NIL)仍未找到目标值,则返回 0。
在 main 函数中,我们创建了一个顺序统计树的示例,并调用 osKeyRank 函数查找值为 12 的结点的秩。如果找到了结点,我们打印结点的秩;否则,打印未找到结点的消息。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号