2023-12-30:用go语言,给你一个下标从 0 开始的整数数组 nums ,它包含 n 个 互不相同 的正整数, 如果 nums 的一个排列满足以下条件,我们称它是一个特别的排列。 对于 0 <
2023-12-30:用go语言,给你一个下标从 0 开始的整数数组 nums ,它包含 n 个 互不相同 的正整数,
如果 nums 的一个排列满足以下条件,我们称它是一个特别的排列。
对于 0 <= i < n - 1 的下标 i:
要么 nums[i] % nums[i+1] == 0,
要么 nums[i+1] % nums[i] == 0。
请你返回特别排列的总数目,由于答案可能很大,请将它对 1000000007 取余 后返回。
输入:nums = [2,3,6]。
输出:2。
来自力扣2741. 特别的排列。
答案2023-12-30:
来自左程云。
大体步骤如下:
1.在main函数中,我们调用了specialPerm函数,并传入nums数组。在这个函数内部,首先计算了nums数组的长度n,然后初始化了一个二维数组dp,用于记录状态的转移。
2.specialPerm函数返回调用process函数的结果,传入了nums、n、0、0和dp作为参数。
3.process函数用于计算满足特殊条件的排列总数。首先,它检查dp数组中是否已经计算了当前状态s和位置p的结果,如果是,则直接返回该结果。
4.接下来,如果状态s表示所有的数字都被使用过,那么将结果设为1,表示找到了一个满足条件的排列。
5.否则,对于给定位置p,遍历每个数字i,如果当前状态s中没有包含数字i,且a[p]能整除a[i]或者a[i]能整除a[p],则递归调用process函数,并将结果加到ans上。
6.最后,将得到的ans存入dp数组中,并返回结果。
整体的时间复杂度:O(n*2^n),其中n是nums数组的长度。对于process函数中的每个状态s以及位置p,最坏情况下都要回溯所有的n个数字,因此是指数级的复杂度。
额外空间复杂度:O(2^n * n),其中dp数组占据了主要的空间,它是一个大小为2^n * n的二维数组。
go完整代码如下:
package main
import "fmt"
var mod = 1000000007
func specialPerm(nums []int) int {
n := len(nums)
dp := make([][]int, 1<<n)
for i := range dp {
dp[i] = make([]int, n)
for j := range dp[i] {
dp[i][j] = -1
}
}
return process(nums, n, 0, 0, dp)
}
func process(a []int, n, s, p int, dp [][]int) int {
if dp[s][p] != -1 {
return dp[s][p]
}
var ans int
if s == (1<<n)-1 {
ans = 1
} else {
for i := 0; i < n; i++ {
if s == 0 || (s&(1<<i) == 0 && (a[p]%a[i] == 0 || a[i]%a[p] == 0)) {
ans = (ans + process(a, n, s|(1<<i), i, dp)) % mod
}
}
}
dp[s][p] = ans
return ans
}
func main() {
nums := []int{2, 3, 6}
result := specialPerm(nums)
fmt.Println("Result:", result)
}
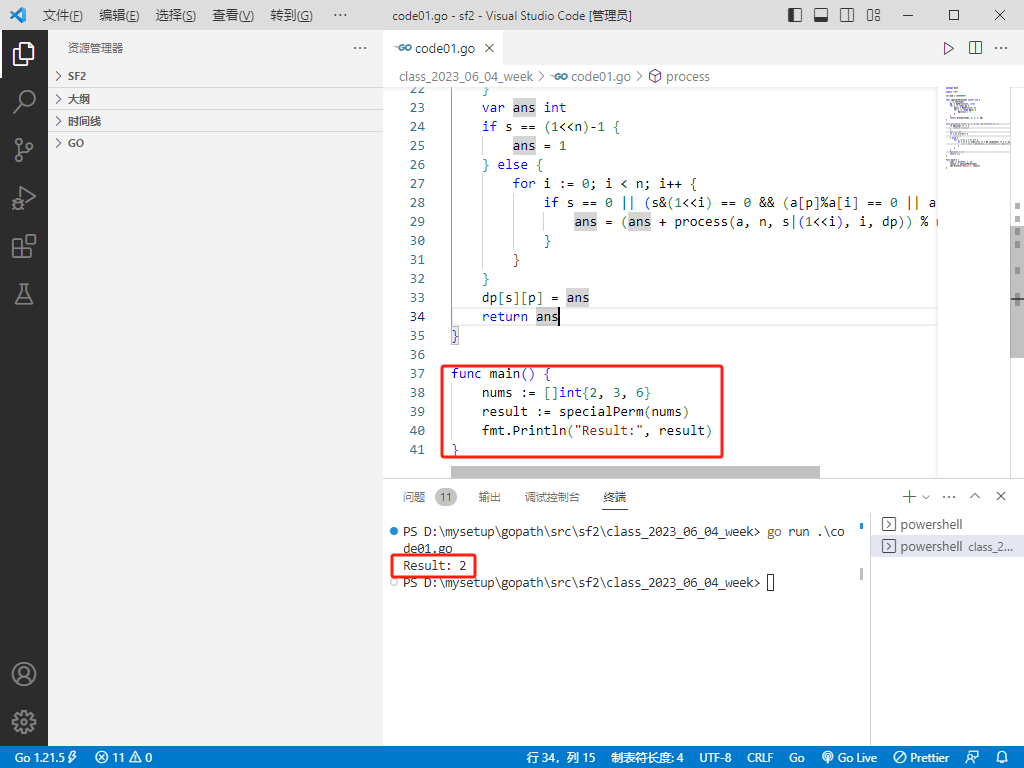
rust完整代码如下:
fn special_perm(nums: Vec<i32>) -> i32 {
let n = nums.len();
let mod_num = 1000000007;
let mut dp = vec![vec![-1; n]; 1 << n];
process(&nums, n, 0, 0, &mut dp, mod_num)
}
fn process(a: &Vec<i32>, n: usize, s: usize, p: usize, dp: &mut Vec<Vec<i32>>, mod_num: i32) -> i32 {
if dp[s][p] != -1 {
return dp[s][p];
}
let ans: i32;
if s == (1 << n) - 1 {
ans = 1;
} else {
ans = (0..n).fold(0, |accum, i| {
if s == 0 || (s & (1 << i) == 0 && (a[p] % a[i] == 0 || a[i] % a[p] == 0)) {
(accum + process(a, n, s | (1 << i), i, dp, mod_num)) % mod_num
} else {
accum
}
});
}
dp[s][p] = ans;
ans
}
fn main() {
let nums = vec![2, 3, 6];
let result = special_perm(nums);
println!("Result: {}", result);
}
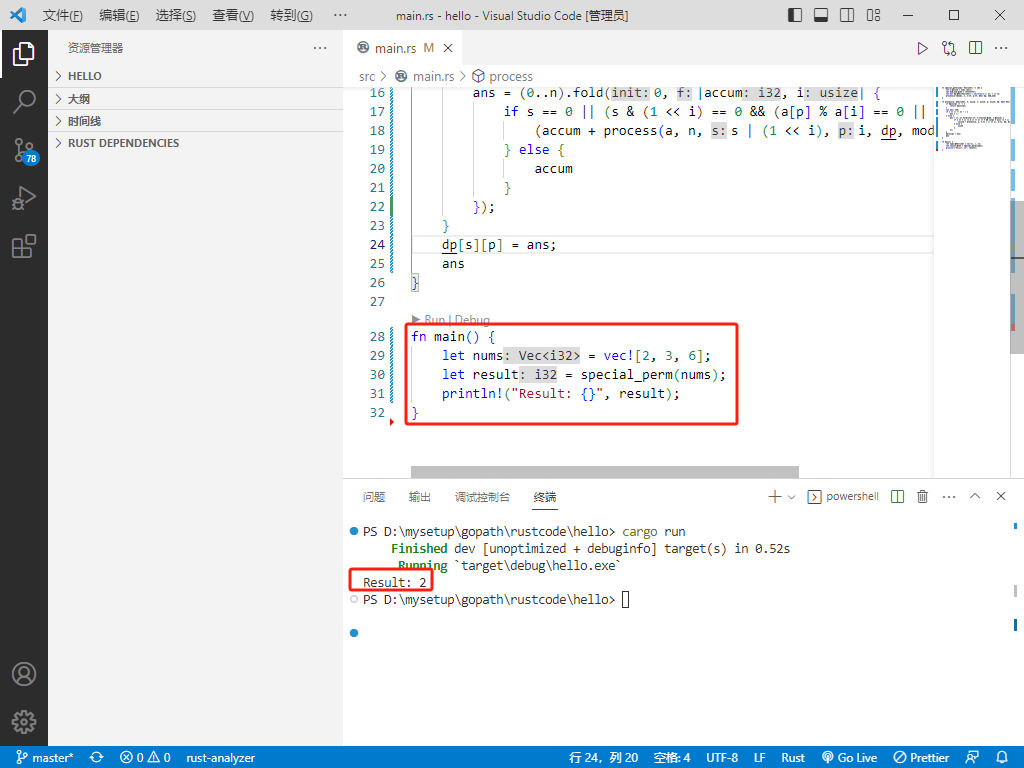
c++完整代码如下:
#include <iostream>
#include <vector>
#include <unordered_map>
using namespace std;
const int mod = 1000000007;
int process(const vector<int>& a, int n, int s, int p, unordered_map<int, unordered_map<int, int>>& dp) {
if (dp.count(s) && dp[s].count(p) != 0) {
return dp[s][p];
}
int ans = 0;
if (s == (1 << n) - 1) {
ans = 1;
}
else {
for (int i = 0; i < n; i++) {
if (s == 0 || (s & (1 << i)) == 0 && (a[p] % a[i] == 0 || a[i] % a[p] == 0)) {
ans = (ans + process(a, n, s | (1 << i), i, dp)) % mod;
}
}
}
dp[s][p] = ans;
return ans;
}
int specialPerm(const vector<int>& nums) {
int n = nums.size();
unordered_map<int, unordered_map<int, int>> dp;
return process(nums, n, 0, 0, dp);
}
int main() {
vector<int> nums = { 2, 3, 6 };
int result = specialPerm(nums);
cout << "Result: " << result << endl;
return 0;
}
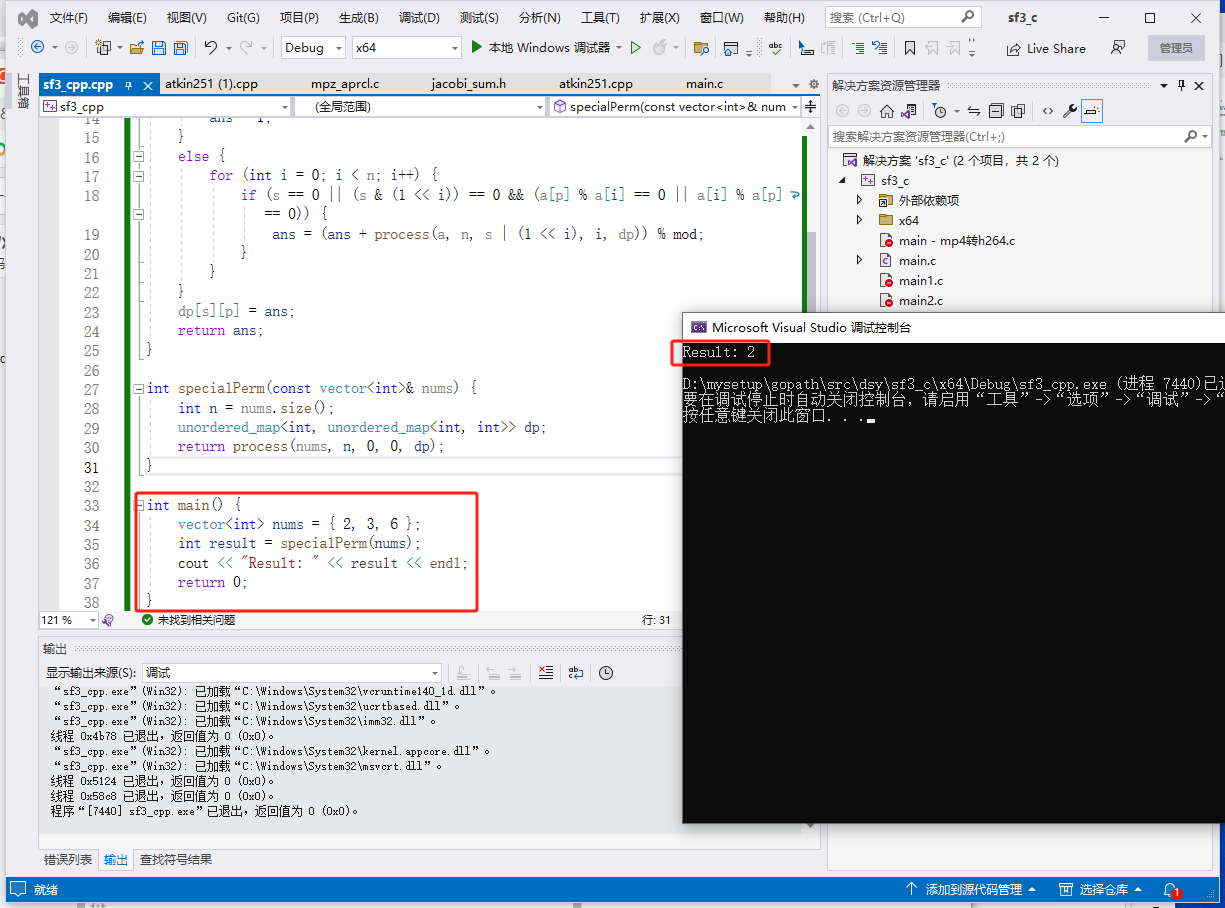
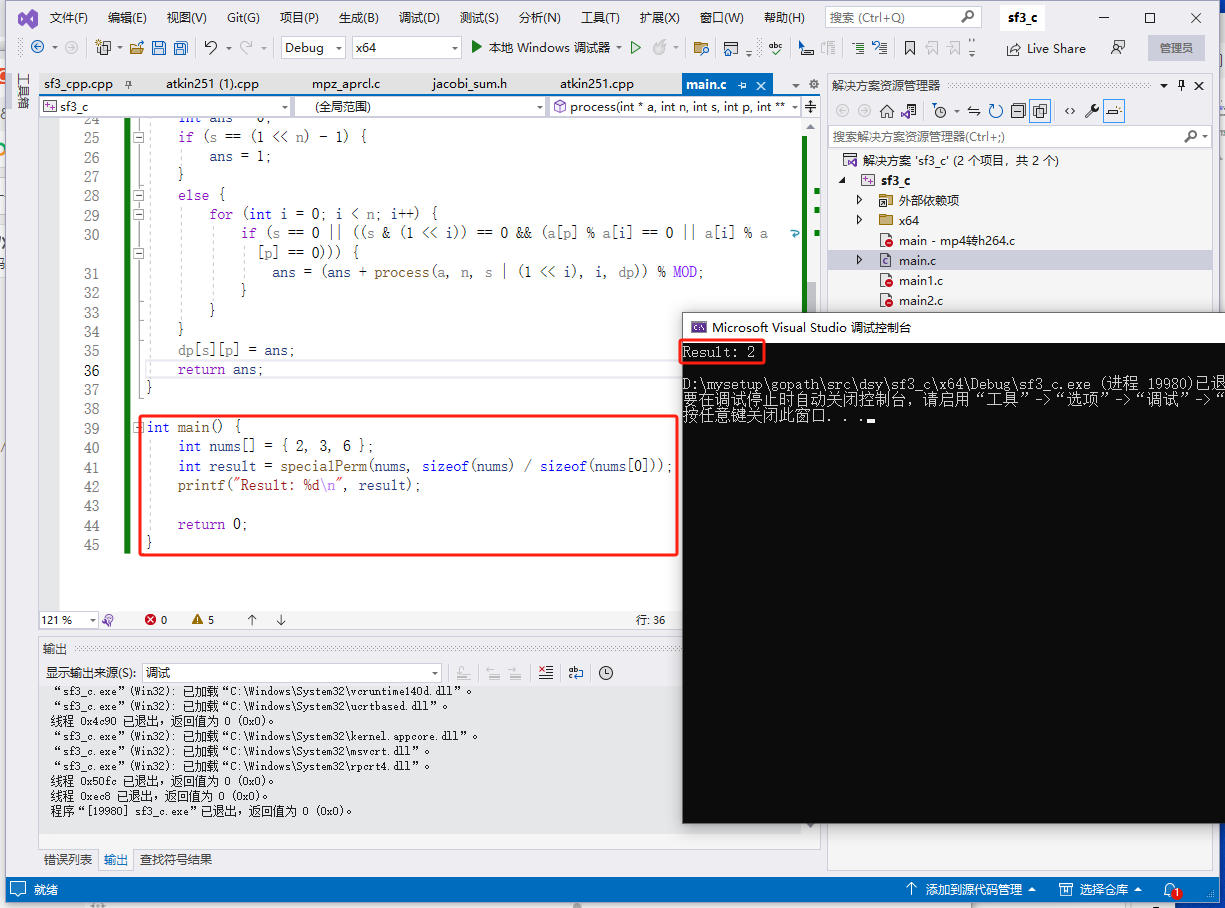
c完整代码如下:
#include <stdio.h>
#include <stdlib.h>
#define MOD 1000000007
int process(int* a, int n, int s, int p, int** dp);
int specialPerm(int* nums, int numsSize) {
int n = numsSize;
int** dp = (int**)malloc((1 << n) * sizeof(int*));
for (int i = 0; i < (1 << n); i++) {
dp[i] = (int*)malloc(n * sizeof(int));
for (int j = 0; j < n; j++) {
dp[i][j] = -1;
}
}
return process(nums, n, 0, 0, dp);
}
int process(int* a, int n, int s, int p, int** dp) {
if (dp[s][p] != -1) {
return dp[s][p];
}
int ans = 0;
if (s == (1 << n) - 1) {
ans = 1;
}
else {
for (int i = 0; i < n; i++) {
if (s == 0 || ((s & (1 << i)) == 0 && (a[p] % a[i] == 0 || a[i] % a[p] == 0))) {
ans = (ans + process(a, n, s | (1 << i), i, dp)) % MOD;
}
}
}
dp[s][p] = ans;
return ans;
}
int main() {
int nums[] = { 2, 3, 6 };
int result = specialPerm(nums, sizeof(nums) / sizeof(nums[0]));
printf("Result: %d\n", result);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号