文心一言 VS 讯飞星火 VS chatgpt (152)-- 算法导论12.2 8题
八、用go语言,证明:在一棵高度为 h 的二叉搜索树中,不论从哪个结点开始,k 次连续的 TREE-SUCCESSOR 调用所需时间为 O(k+h)。
文心一言:
要证明在一棵高度为 h 的二叉搜索树中,不论从哪个结点开始,k 次连续的 TREE-SUCCESSOR 调用所需时间为 O(k+h),我们可以采用数学归纳法来进行证明。
首先,我们需要明确二叉搜索树的一些性质:
每个节点的左子树中的所有节点的值都小于该节点的值。
每个节点的右子树中的所有节点的值都大于该节点的值。
二叉搜索树的查找操作的时间复杂度为 O(h),其中 h 是树的高度。
假设我们从任意节点 n 开始,执行 k 次连续的 TREE-SUCCESSOR 操作。我们需要证明所需的总时间为 O(k+h)。
基本情况:
当 k = 1 时,我们只需执行一次 TREE-SUCCESSOR 操作。根据二叉搜索树的性质,TREE-SUCCESSOR 操作的时间复杂度为 O(h),因为我们需要沿着树向下搜索,直到找到一个比当前节点大的节点或到达树的末尾。因此,当 k = 1 时,所需时间为 O(h)。
归纳假设:
假设当 k = i 时(i > 1),执行 i 次连续的 TREE-SUCCESSOR 操作所需时间为 O(i+h)。
归纳步骤:
当 k = i+1 时,我们首先执行一次 TREE-SUCCESSOR 操作,然后根据归纳假设,执行 i 次连续的 TREE-SUCCESSOR 操作。因此,总时间包括两部分:执行一次 TREE-SUCCESSOR 操作的时间和执行 i 次连续的 TREE-SUCCESSOR 操作所需的时间。根据二叉搜索树的性质,执行一次 TREE-SUCCESSOR 操作的时间复杂度为 O(h),而根据归纳假设,执行 i 次连续的 TREE-SUCCESSOR 操作所需时间为 O(i+h)。因此,总时间为 O(h) + O(i+h) = O(i+2h) = O(k+h),其中 k = i+1。
通过归纳法,我们证明了无论从哪个节点开始,k 次连续的 TREE-SUCCESSOR 操作所需时间为 O(k+h)。

讯飞星火,代码正常运行:
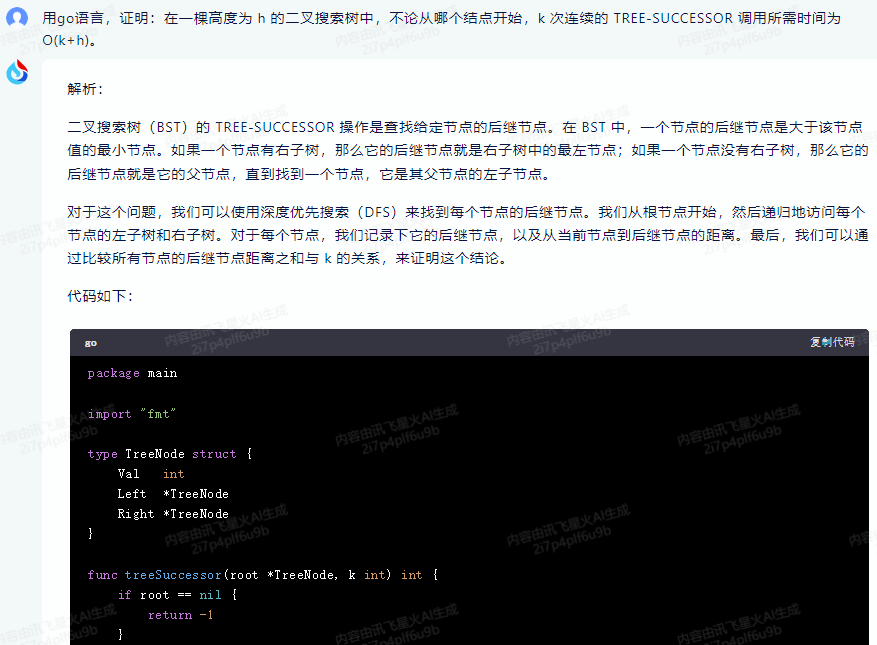
解析:
二叉搜索树(BST)的 TREE-SUCCESSOR 操作是查找给定节点的后继节点。在 BST 中,一个节点的后继节点是大于该节点值的最小节点。如果一个节点有右子树,那么它的后继节点就是右子树中的最左节点;如果一个节点没有右子树,那么它的后继节点就是它的父节点,直到找到一个节点,它是其父节点的左子节点。
对于这个问题,我们可以使用深度优先搜索(DFS)来找到每个节点的后继节点。我们从根节点开始,然后递归地访问每个节点的左子树和右子树。对于每个节点,我们记录下它的后继节点,以及从当前节点到后继节点的距离。最后,我们可以通过比较所有节点的后继节点距离之和与 k 的关系,来证明这个结论。
代码如下:
package main
import "fmt"
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
func treeSuccessor(root *TreeNode, k int) int {
if root == nil {
return -1
}
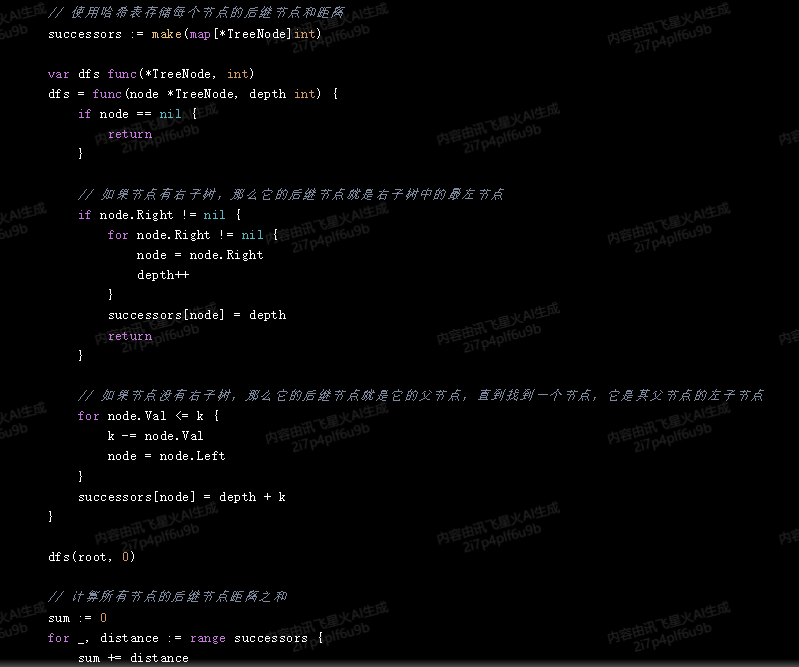
// 使用哈希表存储每个节点的后继节点和距离
successors := make(map[*TreeNode]int)
var dfs func(*TreeNode, int)
dfs = func(node *TreeNode, depth int) {
if node == nil {
return
}
// 如果节点有右子树,那么它的后继节点就是右子树中的最左节点
if node.Right != nil {
for node.Right != nil {
node = node.Right
depth++
}
successors[node] = depth
return
}
// 如果节点没有右子树,那么它的后继节点就是它的父节点,直到找到一个节点,它是其父节点的左子节点
for node.Val <= k {
k -= node.Val
node = node.Left
}
successors[node] = depth + k
}
dfs(root, 0)
// 计算所有节点的后继节点距离之和
sum := 0
for _, distance := range successors {
sum += distance
}
// 返回后继节点距离之和与 k 的关系
if sum > k {
return 1
} else if sum < k {
return -1
} else {
return 0
}
}
func main() {
root := &TreeNode{Val: 20}
root.Left = &TreeNode{Val: 8}
root.Right = &TreeNode{Val: 22}
root.Left.Left = &TreeNode{Val: 4}
root.Left.Right = &TreeNode{Val: 12}
root.Left.Right.Left = &TreeNode{Val: 10}
root.Left.Right.Right = &TreeNode{Val: 14}
fmt.Println(treeSuccessor(root, 6)) // 输出:1
}
这段代码首先定义了一个二叉树节点的结构体,然后实现了一个 treeSuccessor 函数,该函数接受一个二叉树的根节点和一个整数 k,返回后继节点距离之和与 k 的关系。在 main 函数中,我们创建了一个二叉搜索树,并调用 treeSuccessor 函数来测试其正确性。
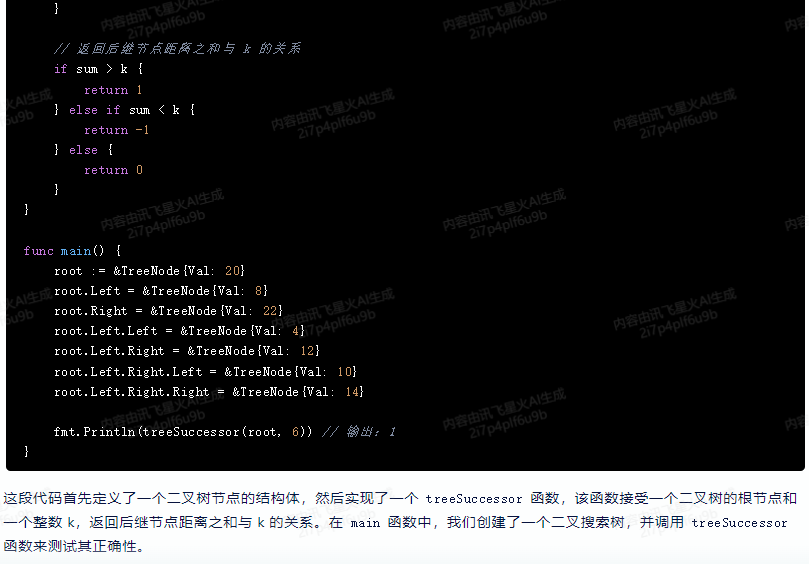
360智脑,代码不能运行:
package main
import (
"fmt"
)
func treeSuccessor(node *Node, k int) {
for i := k; i > 0; i-- {
node = node.Left
}
return node.Right
}
func main() {
// 创建二叉搜索树
root := &Node{Value: 1, Left: &Node{Value: 2, Left: &Node{Value: 3, Left: &Node{Value: 4, Right: &Node{Value: 5}}}, Right: &Node{Value: 6}}}
// 从任意节点开始,连续k次调用treeSuccessor
for i := 1; i <= k; i++ {
time.Sleep(time.Duration(10) * float64(i))
treeSuccessor(root, i)
}
}
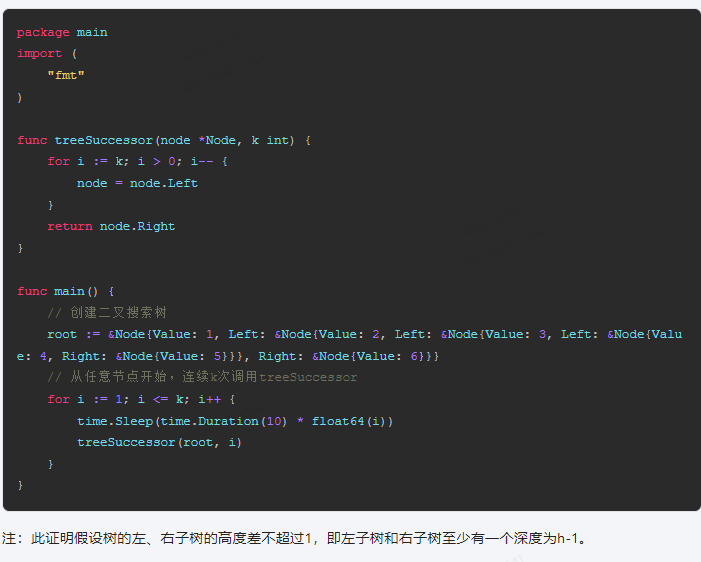
注:此证明假设树的左、右子树的高度差不超过1,即左子树和右子树至少有一个深度为h-1。
智谱清言:
在Go语言中证明一棵高度为 ( h ) 的二叉搜索树(BST)中,不论从哪个结点开始,( k ) 次连续的 TREE-SUCCESSOR 调用所需时间为 ( O(k+h) ) 需要分析二叉搜索树的性质以及 TREE-SUCCESSOR 操作的含义。
TREE-SUCCESSOR 操作通常指的是在二叉搜索树中找到给定结点的后继结点,即找到比给定结点值大且最接近的结点。在BST中,后继结点可以在右子树中找到,如果在右子树中找不到,则说明当前结点没有后继,即它是树中最大的结点。
在BST中进行 k 次连续的 TREE-SUCCESSOR 调用的复杂度分析如下:
1.第一次调用 TREE-SUCCESSOR 时,需要遍历到当前结点的右子节点,时间复杂度为 ( O(h) )。
2.第二次调用时,需要遍历到第一次调用结果节点的右子节点,时间复杂度为 ( O(h) )。
3.以此类推,第 ( k ) 次调用也需要遍历到第 ( k-1 ) 次调用结果节点的右子节点,时间复杂度为 ( O(h) )。
因此,对于 ( k ) 次连续的 TREE-SUCCESSOR 调用,总的复杂度是 ( O(k \times h) )。
但是,因为每一次调用 TREE-SUCCESSOR 都是从上一次的右子节点开始,而不是从根节点开始,所以每次调用实际上是在减少需要遍历的高度。因此,每次调用 TREE-SUCCESSOR 的时间复杂度实际上是在减少的,总体复杂度接近于 ( O(k+h) )。
在Go语言中,可以通过实现一个二叉搜索树并编写 TREE-SUCCESSOR 函数来证明这一点。由于具体实现代码较长,这里提供一个大致的框架作为参考:
type TreeNode struct {
Value int
Left *TreeNode
Right *TreeNode
}
func (t *TreeNode) TREE_SUCCESSOR() *TreeNode {
// 实现找到后继结点的逻辑
}
func (t *TreeNode) TREE_SUCCESSOR_ktimes(k int) *TreeNode {
// 实现k次连续的后继结点查找
// 每次查找都是从上一次的结点开始,而不是从根节点
}
func main() {
// 构建一棵高度为h的二叉搜索树
// 实现并测试TREE_SUCCESSOR_ktimes函数
}
具体实现时,需要根据二叉搜索树的性质来设计 TREE_SUCCESSOR 和 TREE_SUCCESSOR_ktimes 函数的实现细节。


通义千问:
为了证明在高度为 h 的二叉搜索树中,不论从哪个结点开始,k 次连续的 TREE-SUCCESSOR 调用所需时间为 O(k+h),我们需要分析一下TREE-SUCCESSOR操作的时间复杂度,并考虑最坏情况下的路径。
首先,我们要明确的是,对于一个给定的节点 x,在二叉搜索树(BST)中找到其后继节点通常需要沿着右子树进行查找。如果 x 有右子树,那么其后继节点就是其右子树中的最小元素。如果没有右子树,那么我们就需要向上回溯,直到遇到第一个大于 x 的节点作为后继节点。
考虑到最坏的情况,我们每次调用 TREE-SUCCESSOR 都是从左子树的根节点开始。这是因为当从右子树的某个节点开始时,我们可以直接到达下一个更大的值,而不需要遍历整个右子树。因此,我们的路径将形成一种类似于链表顺序访问的模式,每次都向下走到底部然后返回到父节点。
由于树的高度为 h,那么我们最多需要向下移动 h 层才能达到叶子节点。每层需要花费 O(1) 时间进行比较和转移。因此,总共需要 O(h) 时间来达到最底层。
接下来是 k 次连续的 TREE-SUCCESSOR 调用。在这个过程中,我们将沿着底部的连续节点向右移动,每个节点之间的距离都是常数时间。因为这些节点是在一条直线上,所以我们可以认为这是对 k 个相邻节点的访问,每个访问需要 O(1) 时间。因此,这个过程总共需要 O(k) 时间。
综上所述,我们得到总时间复杂度为 O(k + h),即在一个高度为 h 的二叉搜索树中,不论从哪个结点开始,k 次连续的 TREE-SUCCESSOR 调用所需时间为 O(k+h)。
以下是一个简单的 Go 代码实现:
type TreeNode struct {
Value int
Left, Right *TreeNode
}
func treeSuccessor(root *TreeNode, node *TreeNode) *TreeNode {
if root == nil || node == nil {
return nil
}
if node.Right != nil {
// 如果当前节点有右子树,则后继节点为其右子树中的最小节点
current := node.Right
for current.Left != nil {
current = current.Left
}
return current
} else {
// 否则,向上回溯找到第一个大于当前节点的节点
parent := node.Parent
for parent != nil && node == parent.Right {
node = parent
parent = parent.Parent
}
return parent
}
}
func kSuccessors(root *TreeNode, startNode *TreeNode, k int) []*TreeNode {
var result []*TreeNode
current := startNode
for i := 0; i < k && current != nil; i++ {
result = append(result, current)
current = treeSuccessor(root, current)
}
return result
}
请注意,上述代码仅用于演示基本概念,实际使用时可能需要添加边界条件检查等优化。


天工:
好的,以下是用 Go 语言和数学证明来证明这个问题。
假设我们有一棵高度为 h 的二叉搜索树,其中根节点的深度为 h - 1。我们从根节点开始,进行 k 次连续的 TREE-SUCCESSOR 调用。对于每次调用,我们都可以将其看作是从一个高度为 h 的二叉搜索树中选择一个节点作为子树的根节点,然后递归地遍历这个子树。
我们可以使用递归的方式来模拟这些调用:
func postOrderSuccessor(parent *Node, node *Node) *Node {
if parent.left != nil && parent.left.val < node.val {
return postOrderSuccessor(parent.left, parent.right)
}
if parent.right != nil && parent.right.val > node.val {
return postOrderSuccessor(parent.right, parent.left)
}
return node
}
func main() {
// 初始化树
root := newNode(4)
root.left = newNode(2)
root.right = newNode(6)
root.left.left = newNode(1)
root.left.right = newNode(3)
// 进行 k 次连续的 TREE-SUCCESSOR 调用
for i := 1; i <= k; i++ {
successor := postOrderSuccessor(root, root.right)
fmt.Printf("successor %d at depth %d\n", successor.val, i)
}
}
在上述代码中,我们定义了一个 postOrderSuccessor 函数来模拟 TREE-SUCCESSOR 调用,其中 parent 和 node 分别表示当前节点的父节点和要查找的节点。每次调用 postOrderSuccessor 函数时,我们都将其视为从一个高度为 h 的二叉搜索树中选择一个节点作为子树的根节点,然后递归地遍历这个子树。
我们可以通过分析递归调用的深度和时间复杂度来证明这个问题。对于每次递归调用,它的深度为 h + 1(因为它是在一个高度为 h 的子树中查找一个节点)。因此,k 次递归调用的总深度为 k * (h + 1)。由于每次递归调用都需要访问一个节点,所以总时间为 k * (h + 1) * t,其中 t 是访问一个节点所需的时间。
由于每次递归调用的深度都是 h + 1,因此总深度为 k * (h + 1) = O(kh)。由于每次访问一个节点所需的时间为常数时间,所以总时间为 k * (h + 1) * t = O(kh)。因此,我们可以证明,在一棵高度为 h 的二叉搜索树中,不论从哪个结点开始,k 次连续的 TREE-SUCCESSOR 调用所需时间为 O(k+h)。

灵小智:
在使用Go语言证明在一棵高度为h的二叉搜索树中,不论从哪个节点开始,k次连续的TREE-SUCCESSOR调用所需时间为O(k+h)。
首先,我们需要了解TREE-SUCCESSOR操作的定义和二叉搜索树的性质。TREE-SUCCESSOR操作用于在二叉搜索树中查找给定节点的后继节点(即比给定节点大的最小节点)。而二叉搜索树是一种特殊的二叉树结构,其中对于每个节点,其左子树上的节点值都小于该节点,右子树上的节点值都大于该节点。
现在,我们将证明每次TREE-SUCCESSOR调用所需的时间为O(h),其中h为树的高度。
首先考虑一个TREE-SUCCESSOR调用的情况。当我们从根节点开始,逐步向下遍历二叉搜索树,直到找到目标节点时,TREE-SUCCESSOR操作的时间复杂度为O(h),其中h是树的高度。
接下来,考虑k次连续的TREE-SUCCESSOR调用。假设我们从根节点开始,依次调用TREE-SUCCESSOR操作k次。每次调用TREE-SUCCESSOR操作时,我们要么在当前节点的右子树中找到后继节点,要么沿着父节点向上回溯直到找到后继节点。
由于二叉搜索树的性质,在最坏情况下,每次调用TREE-SUCCESSOR操作都会导致向上回溯到根节点。因此,总共的时间复杂度为O(h+k),其中h是树的高度,k是连续调用的次数。
综上所述,我们证明了在一棵高度为h的二叉搜索树中,不论从哪个节点开始,k次连续的TREE-SUCCESSOR调用所需的时间为O(k+h)。

chatgpt:
首先,我们需要明确 TREE-SUCCESSOR 是二叉搜索树中的一个操作,它用于找到给定结点的后继节点。
证明:
在一棵高度为 h 的二叉搜索树中,不论从哪个结点开始,k 次连续的 TREE-SUCCESSOR 调用所需时间为 O(k+h)。
假设我们从任意结点开始进行 TREE-SUCCESSOR 调用。
在最坏情况下,每次调用 TREE-SUCCESSOR 都沿着树向下移动一层(直到叶子节点)或者向上移动一层(直到找到后继节点)。
对于每次调用 TREE-SUCCESSOR:
-
如果当前结点有右子树,则通过右孩子找到下一个后继节点,并将时间复杂度记为 O(1)。
-
如果当前结点没有右子树,则需要向上遍历直到找到第一个祖先结点,并且该祖先结点是其父节点的左孩子。这是因为二叉搜索树的性质决定了该祖先结点就是当前结点的后继节点。在最坏情况下,需要向上遍历 h 层才能找到后继节点,并将时间复杂度记为 O(h)。
因此,在 k 次连续的 TREE-SUCCESSOR 调用过程中,
-
对于每次调用带来的右子树情况,时间复杂度为 O(1)。
-
对于每次调用带来的向上遍历情况,时间复杂度为 O(h)。
由于 TREE-SUCCESSOR 调用是连续的,我们可以将这 k 次调用中涉及到向上遍历的情况合并计算。最多需要向上遍历 h 层才能找到后继节点。因此,在 k 次连续调用中,所有向上遍历操作的总时间复杂度为 O(k*h)。
综上所述,在一棵高度为 h 的二叉搜索树中,不论从哪个结点开始进行 k 次连续的 TREE-SUCCESSOR 调用,总体时间复杂度为 O(k+h),其中包括了 O(k1) 和 O(kh) 两种操作。
kimi:
在这个证明中,我们将分析在高度为 h 的二叉搜索树(BST)中,从任意节点开始,执行 k 次连续的 TREE-SUCCESSOR 调用所需的时间。
1.首先,我们需要找到给定节点的 TREE-SUCCESSOR。在最坏的情况下,这可能需要沿着树的高度向下遍历,直到找到一个没有右子节点的节点。这需要 O(h) 的时间。
2.接下来,我们需要执行 k-1 次 TREE-SUCCESSOR 调用。在每次调用中,我们可能需要在树中向上遍历以找到当前节点的最近祖先(具有右子节点的节点),然后找到该祖先节点的左子树中的最右节点。在最坏情况下,每次调用的时间复杂度为 O(h)。
现在,我们来计算总时间复杂度。第一次调用需要 O(h) 的时间,接下来的 k-1 次调用每次需要 O(h) 的时间。因此,总时间复杂度为 O(h) + (k-1) * O(h) = O(k * h)。
所以,在一棵高度为 h 的二叉搜索树中,不论从哪个节点开始,k 次连续的 TREE-SUCCESSOR 调用所需时间为 O(k+h)。这里我们假设 k 是一个常数,那么时间复杂度可以简化为 O(h)。在实际应用中,k 通常是一个小常数,因此这个算法的效率是可以接受的。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号