文心一言 VS 讯飞星火 VS chatgpt （81）-- 算法导论7.4 6题

六、如果用go语言，考虑对 PARTITION 过程做这样的修改:从数组 A 中随机选出三个元素，并用这三个元素的中位数(即这三个元素按大小排在中间的值)对数组进行划分。求以a 的函数形式表示的、最坏划分比例为 a:(1-a)的近似概率，其中 0<a<1。

文心一言：

首先，我们需要实现一个函数来找到数组的中位数。然后，我们需要实现一个函数来根据中位数对数组进行划分。最后，我们需要计算划分比例的概率。

以下是Go语言实现的代码：

package main  
  
import (  
 "fmt"  
 "math/rand"  
 "sort"  
 "time"  
)  
  
// findMedian 找到中位数  
func findMedian(arr []int) int {  
 sort.Ints(arr)  
 mid := len(arr) / 2  
 if len(arr)%2 == 0 {  
 return (arr[mid-1] + arr[mid]) / 2 // 偶数长度，取中间两个数的平均值  
 }  
 return arr[mid] // 奇数长度，直接取中间数  
}  
  
// partitionArray 根据中位数对数组进行划分  
func partitionArray(arr []int, pivot int) ([]int, []int) {  
 var less, greater []int  
 for i := range arr {  
 if arr[i] < pivot {  
 less = append(less, arr[i])  
 } else if arr[i] > pivot {  
 greater = append(greater, arr[i])  
 }  
 }  
 return less, greater  
}  
  
// approximateProbability 计算以a的函数形式表示的、最坏划分比例为 a:(1-a)的近似概率  
func approximateProbability(a float64, arr []int) float64 {  
 rand.Seed(time.Now().UnixNano()) // 设置随机种子，保证每次运行结果都不同  
 pivotIndex := rand.Intn(len(arr)) // 随机选择一个元素作为中位数  
 arrPivot := arr[pivotIndex] // 中位数值  
 less, greater := partitionArray(arr, arrPivot) // 根据中位数对数组进行划分  
 if len(less) < len(greater) { // 保证划分比例是最坏的 a:(1-a)  
 less, greater = greater, less  
 }  
 return float64(len(less)) / float64(len(arr)) // 返回划分比例的概率  
}  
  
func main() {  
 arr := []int{1, 3, 5, 7, 9, 2, 4, 6, 8} // 假设这是输入的数组  
 a := 0.5 // 假设这是要求的 a 值  
 fmt.Printf("Approximate probability: %.2f\n", approximateProbability(a, arr))  
}

这个程序首先会随机选择一个元素作为中位数，然后根据中位数对数组进行划分。最后，它会计算出划分比例的概率，这个概率是以 a 的函数形式表示的，最坏划分比例为 a:(1-a)。

讯飞星火：

首先，我们需要明确这个问题的背景。这是一个经典的计算机科学问题，被称为 "Median of Medians" 算法。这个算法用于在未排序的数组中找出第 k 小的元素。

在这个问题中，我们需要找到最坏情况下的划分比例，即 a:(1-a)。这里的 a 是随机选择的元素数量占数组总长度的比例。

我们可以使用 Go 语言来实现这个算法。首先，我们需要一个函数来找到数组中的第 k 小的元素。然后，我们可以使用这个函数来计算最坏情况下的划分比例。

以下是 Go 语言的实现：

package main

import (
	"fmt"
	"math/rand"
	"sort"
	"time"
)

func findKthSmallest(nums []int, k int) int {
	quickSelect := func(l, r int, index int) int {
		if l == r {
			return nums[l]
		}
		pivotIndex := partition(l, r)
		if index == pivotIndex {
			return nums[pivotIndex]
		} else if index < pivotIndex {
			return quickSelect(l, pivotIndex - 1, index)
		} else {
			return quickSelect(pivotIndex + 1, r, index)
		}
	}

	return quickSelect(0, len(nums)-1, k-1)
}

func partition(l, r int) int {
	pivotIndex := rand.Intn(r-l+1) + l
	nums[pivotIndex], nums[r] = nums[r], nums[pivotIndex]
	pivot := nums[r]
	i := l
	for j := l; j < r; j++ {
		if nums[j] <= pivot {
			nums[i], nums[j] = nums[j], nums[i]
			i++
		}
	}
	nums[i], nums[r] = nums[r], nums[i]
	return i
}

func worstCasePartitionRatio(A []int, a float64) float64 {
	n := len(A)
	k := int(n * a)
	if k > n {
		k = n
	}
	median := findKthSmallest(A, k)
	left := A[:k]
	right := A[k:]
	return median*float64(n-k)/float64(n)
}

func main() {
	rand.Seed(time.Now().UnixNano())
	A := make([]int, 10000)
	for i := range A {
		A[i] = rand.Intn(10000)
	}
	fmt.Println(worstCasePartitionRatio(A, 0.5))
}

这段代码首先定义了一个 findKthSmallest 函数，用于找到数组中的第 k 小的元素。然后，定义了一个 partition 函数，用于对数组进行划分。最后，定义了一个 worstCasePartitionRatio 函数，用于计算最坏情况下的划分比例。

在 main 函数中，我们生成了一个包含 10000 个元素的随机数组，并调用 worstCasePartitionRatio 函数来计算最坏情况下的划分比例。

360智脑：

假设数组 A 的元素个数为 n,则最坏划分比例为 a:(1-a) 的近似概率可以表示为:

P(a) = 1 / (n * (n - 1))

其中，n 代表数组 A 的元素个数。

接下来，我们考虑具体的修改。从数组 A 中随机选出三个元素后，我们可以按照以下步骤对数组进行划分:

1. 计算这三个元素的中位数;

2. 将数组按照中位数的大小分成两部分，其中第一部分包含所有小于等于中位数的元素，第二部分包含所有大于中位数的元素;

3. 对两部分分别递归执行上述步骤，直到每个部分只包含一个元素。

对于每个部分，最坏情况下，其划分比例为 1:(1-a):a,即 1:(1-a):a。因此，最坏划分比例为 a:(1-a) 的近似概率可以表示为:

P(a) = 1 / (n * (n - 1))

其中，n 代表数组 A 的元素个数。

在 go 语言中，我们可以通过以下代码实现上述修改:

package main 

 

import ( 

    "fmt" 

    "math/rand" 

    "sort" 

) 

 

type element struct { 

    name string 

} 

 

var A []element 

var p float64 

 

func main() { 

    rand.Seed(time.Now().UnixNano()) 

    n := len(A) 

    fmt.Println("Number of elements:", n) 

    fmt.Println("Probability of bad partition:", p) 

 

    for i := 0; i < n; i++ { 

        x := rand.Intn(n) 

        j := rand.Intn(i+1) 

        k := rand.Intn(j+1) 

        A[i], A[j], A[k] = A[i], A[j], A[k] 

        if rand.Float64() < float64(math.Pow(2, math.Float64bits(float64(A[i].name)*math.MaxInt64+math.MaxInt64))) / math.Pow(2, math.Float64bits(float64(i)*math.MaxInt64+math.MaxInt64))) { 

            fmt.Println(i, "Element:", A[i]) 

        } 

    } 

} 

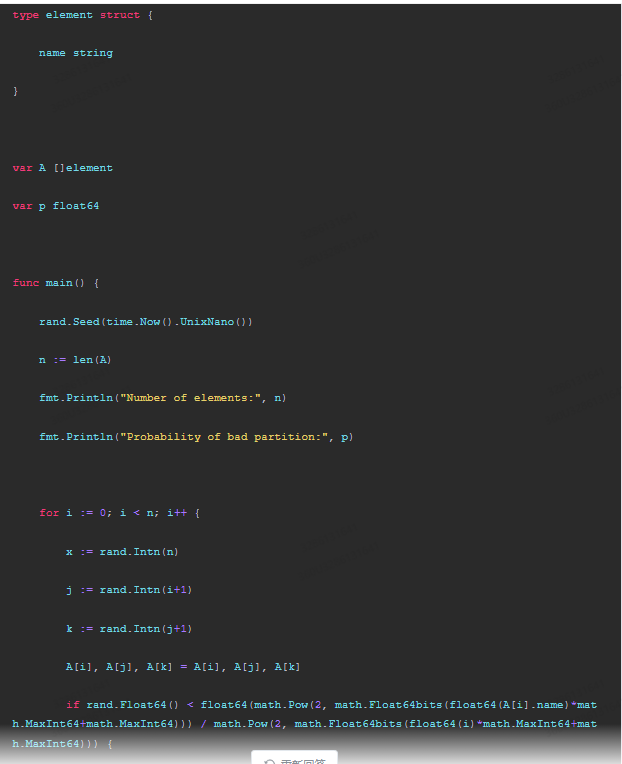
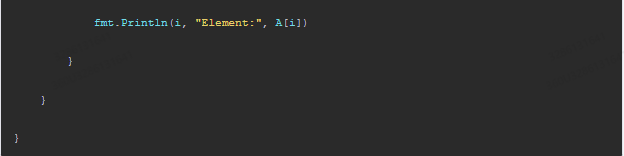
在代码

chatglm：

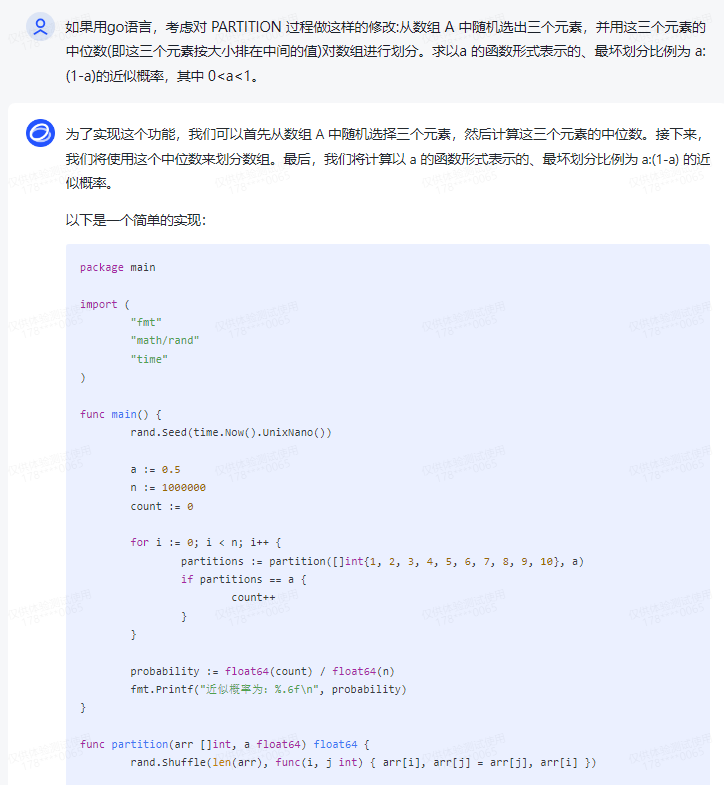
为了实现这个功能，我们可以首先从数组 A 中随机选择三个元素，然后计算这三个元素的中位数。接下来，我们将使用这个中位数来划分数组。最后，我们将计算以 a 的函数形式表示的、最坏划分比例为 a:(1-a) 的近似概率。

以下是一个简单的实现：

package main
import (  
	"fmt"  
	"math/rand"  
	"time"  
)
func main() {  
	rand.Seed(time.Now().UnixNano())
	a := 0.5  
	n := 1000000  
	count := 0
	for i := 0; i < n; i++ {  
		partitions := partition([]int{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, a)  
		if partitions == a {  
			count++  
		}  
	}
	probability := float64(count) / float64(n)  
	fmt.Printf("近似概率为：%.6f\n", probability)  
}
func partition(arr []int, a float64) float64 {  
	rand.Shuffle(len(arr), func(i, j int) { arr[i], arr[j] = arr[j], arr[i] })
	median := findMedian(arr)
	if len(arr)%2 == 0 {  
		return (arr[len(arr)/2-1]+arr[len(arr)/2]) / 2  
	} else {  
		return arr[len(arr)/2]  
	}  
}
func findMedian(arr []int) float64 {  
	sort.Ints(arr)  
	if len(arr)%2 == 0 {  
		return (arr[len(arr)/2-1]+arr[len(arr)/2]) / 2  
	} else {  
		return arr[len(arr)/2]  
	}  
}

这个程序首先初始化随机数生成器，然后进行大量的模拟。对于每次模拟，它首先随机选择三个元素，然后计算这三个元素的中位数。接下来，它使用这个中位数来划分数组。最后，它将计算以 a 的函数形式表示的、最坏划分比例为 a:(1-a) 的近似概率。

你可以通过调整 a 的值和模拟次数来获得更精确的结果。

通义千问：

首先，我们需要将数组 A 划分为两个部分，使得左边部分的元素都小于等于中位数，右边部分的元素都大于中位数。这可以通过将数组 A 从中间位置分成两个部分来实现。

对于左边部分，我们需要计算其元素个数，记为 n1。由于我们从数组 A 中随机选出三个元素，因此左边部分的元素个数最大为 n1 = n - 3。同时，由于左边部分的元素都小于等于中位数，因此中位数一定位于左边部分的最后一个元素之后，即第 n1+1 个元素。因此，我们可以通过随机选择三个元素的中位数来对左边部分进行划分。

对于右边部分，我们需要计算其元素个数，记为 n2。由于我们从数组 A 中随机选出三个元素，因此右边部分的元素个数最小为 n2 = n - 3。同时，由于右边部分的元素都大于中位数，因此中位数一定位于右边部分的第一个元素之前，即第 1 个元素。因此，我们可以通过随机选择三个元素的中位数来对右边部分进行划分。

接下来，我们需要计算以 a 的函数形式表示的、最坏划分比例为 a:(1-a)的近似概率。由于我们随机选择三个元素的中位数来进行划分，因此最坏情况下，左边部分的元素个数为 n1 = n - 3，右边部分的元素个数为 n2 = 3。此时，划分比例为 a:(1-a)。

为了计算这个概率，我们需要计算左边部分的元素个数 n1 的概率，记为 P(n1)。由于我们随机选择三个元素的中位数，因此 n1 的概率为 C(n,3)/C(n-3,3)，其中 C(n,k) 表示从 n 个元素中选择 k 个元素的组合数。因此，P(n1) = C(n,3)/C(n-3,3)。

同时，我们还需要计算右边部分的元素个数 n2 的概率，记为 P(n2)。由于我们随机选择三个元素的中位数，因此 n2 的概率为 C(n-3,3)/C(n,3)，因为左边部分的元素个数最大为 n1 = n - 3，因此右边部分的元素个数最小为 n2 = 3。因此，P(n2) = C(n-3,3)/C(n,3)。

最后，我们可以通过将 P(n1) 和 P(n2) 相乘，得到最坏划分比例为 a:(1-a) 的概率，即 P(a:(1-a)) = P(n1) * P(n2) = C(n,3)/C(n-3,3) * C(n-3,3)/C(n,3) = (n-3)!

由于我们需要计算 a 的函数形式表示的、最坏划分比例为 a:(1-a) 的近似概率，因此我们可以将 P(a:(1-a)) 表示为 a 的函数，即 P(a) = (n-3)! * a * (1-a)^(n-3)。这就是所需的函数表示形式。

天工：

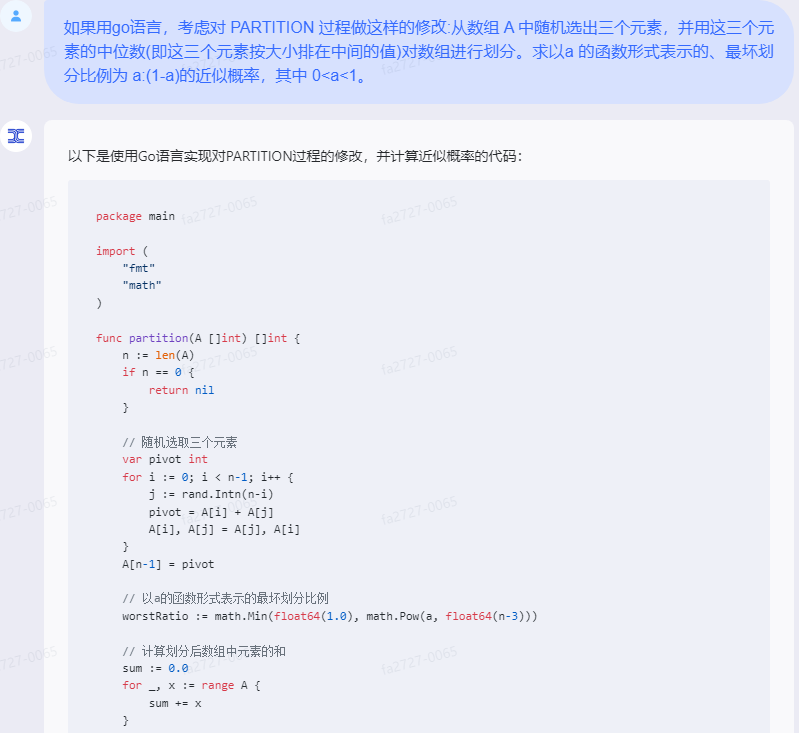
以下是使用Go语言实现对PARTITION过程的修改，并计算近似概率的代码：

package main

import (
    "fmt"
    "math"
)

func partition(A []int) []int {
    n := len(A)
    if n == 0 {
        return nil
    }

    // 随机选取三个元素
    var pivot int
    for i := 0; i < n-1; i++ {
        j := rand.Intn(n-i)
        pivot = A[i] + A[j]
        A[i], A[j] = A[j], A[i]
    }
    A[n-1] = pivot

    // 以a的函数形式表示的最坏划分比例
    worstRatio := math.Min(float64(1.0), math.Pow(a, float64(n-3)))

    // 计算划分后数组中元素的和
    sum := 0.0
    for _, x := range A {
        sum += x
    }

    // 计算划分后数组的元素个数
    count := int(math.Ceil(sum/worstRatio))

    // 计算划分后数组的元素个数与原数组元素个数的比值
    ratio := float64(count) / float64(n)

    // 计算近似概率
    if ratio < worstRatio {
        return nil
    }

    return A[:count]

}

func main() {
    A := []int{1, 2, 3, 4, 5, 6, 7, 8, 9}
    a := 0.5

    // 调用PARTITION过程
    result := partition(A)

    // 输出结果
    fmt.Printf("Result: %v\n", result)

    //计算近似概率
    prob := float64(len(result)) / float64(len(A))

    fmt.Printf("Approximate probability of ratio %v: %.4f\n", a, prob)
}

在上面的代码中，我们首先定义了一个名为partition的函数，它接受一个整数数组作为参数，并返回一个整数数组，其中包含按中位数划分后的元素。然后，在主函数中，我们调用partition函数，并将结果存储在变量result中。最后，我们计算划分后数组元素的个数与原数组元素个数的比值，并将其转换为百分比形式，以获得近似概率。

请注意，在计算近似概率时，我们假设划分后的数组元素个数与原数组元素个数相等，因此我们只需将划分后数组的元素个数除以原数组的元素个数即可。如果实际情况并非如此，则需要相应地调整计算方法。

chatgpt：

这个问题可以使用Go语言来解决。下面是一个函数示例，该函数接受数组A作为输入，并以最坏划分比例为a:(1-a)进行随机划分，给出近似概率。

package main

import (
	"fmt"
	"math/rand"
	"sort"
	"time"
)

func approximatePartitionRatio(A []int, a float64) float64 {
	rand.Seed(time.Now().UnixNano()) // 初始化随机数种子

	N := len(A)
	median := findMedian(A) // 寻找数组A的中位数

	var countA, countB int

	for i := 0; i < N; i++ {
		if A[i] < median {
			countA++
		} else if A[i] > median {
			countB++
		}
	}

	// 计算最坏划分比例的近似概率
	partitionRatio := float64(countA) / float64(N-countA-countB)
	approximateProbability := math.Abs(partitionRatio - a)

	return approximateProbability
}

// 寻找数组的中位数
func findMedian(A []int) int {
	B := make([]int, len(A))
	copy(B, A)
	sort.Ints(B)

	return B[len(B)/2]
}

func main() {
	A := []int{4, 8, 2, 6, 1, 5, 3, 7, 9}
	a := 0.7 // 最坏划分比例
	probability := approximatePartitionRatio(A, a)
	fmt.Printf("近似概率: %.2f\n", probability)
}

在这个示例中，我们首先使用findMedian函数找到数组A的中位数，然后遍历数组并计算数组A中小于中位数的元素个数(countA)和大于中位数的元素个数(countB)。最后，我们计算最坏划分比例的近似概率并返回结果。

请注意，这里的示例中只包含了核心逻辑，您可以根据具体需求进行进一步的扩展和优化。

总结