2023-08-02:给定一棵树,一共有n个点, 每个点上没有值,请把1~n这些数字,不重复的分配到二叉树上, 做到 : 奇数层节点的值总和 与 偶数层节点的值总和 相差不超过1。 返回奇数层节点分配
2023-08-02:给定一棵树,一共有n个点,
每个点上没有值,请把1~n这些数字,不重复的分配到二叉树上,
做到 : 奇数层节点的值总和 与 偶数层节点的值总和 相差不超过1。
返回奇数层节点分配值的一个方案。
2 <= n <= 10^5 。
来自腾讯音乐。
答案2023-08-02:
大致步骤如下:
1.计算出1到n的总和sum。
2.确定两个目标值p1和p2,它们分别是sum的整数除法结果和向上取整结果。p1和p2代表了奇数层节点总和和偶数层节点总和的一半。
3.调用generate函数来生成奇数层节点的分配方案。generate函数用于生成一个数组,其中包含k个数,这k个数的和为指定的wantSum。如果无法生成满足要求的方案,则返回nil。
4.如果generate函数返回nil并且sum是奇数,说明无法找到满足要求的奇数层节点方案。这种情况下,重新调用generate函数来生成偶数层节点的分配方案。
5.如果两次调用generate函数都没有找到满足要求的方案,则返回[-1]表示无解。
6.输出生成的方案。
时间复杂度分析:
-
计算sum的时间复杂度为O(1)。
-
generate函数的时间复杂度为O(k)。
-
整体时间复杂度为O(k)。
空间复杂度分析:
-
generate函数中创建了一个大小为k的数组来存储结果,所以空间复杂度为O(k)。
-
整体空间复杂度为O(k)。
go完整代码如下:
package main
import "fmt"
// generate returns an array of k numbers between 1 and n whose sum is wantSum
func generate(wantSum, n, k int) []int {
// The minimum sum of k numbers, for example: 1 2 3 ... k
sumMinK := (k + 1) * k / 2
// The range each number can increase
rangeVal := n - k
if wantSum < sumMinK || wantSum > sumMinK+k*rangeVal {
return nil
}
add := wantSum - sumMinK
rightSize := add / rangeVal
midIndex := (k - rightSize) + (add % rangeVal)
leftSize := k - rightSize
if add%rangeVal != 0 {
leftSize--
}
ans := make([]int, k)
for i := 0; i < leftSize; i++ {
ans[i] = i + 1
}
if add%rangeVal != 0 {
ans[leftSize] = midIndex
}
for i, j := k-1, 0; j < rightSize; i, j = i-1, j+1 {
ans[i] = n - j
}
return ans
}
// team returns the values of the odd nodes out of 1 to n, with a total of k nodes
func team(n, k int) []int {
sum := (n + 1) * n / 2
p1 := sum / 2
p2 := (sum + 1) / 2
ans := generate(p1, n, k)
if ans == nil && (sum&1) == 1 {
ans = generate(p2, n, k)
}
if ans == nil {
ans = []int{-1}
}
return ans
}
func main() {
// n is the maximum value, includes 1 to n
n := 100
// k is the number of nodes
k := 33
// Can we approximate half the sum of 1 to n by selecting k nodes? Return the solution.
ans := team(n, k)
fmt.Println("Sum:", (n+1)*n/2)
fmt.Println("Length:", len(ans))
sum := 0
fmt.Print("Numbers:")
for _, num := range ans {
fmt.Print(num, " ")
sum += num
}
fmt.Println()
fmt.Println("Sum:", sum)
fmt.Println("Remaining:", (n+1)*n/2-sum)
}
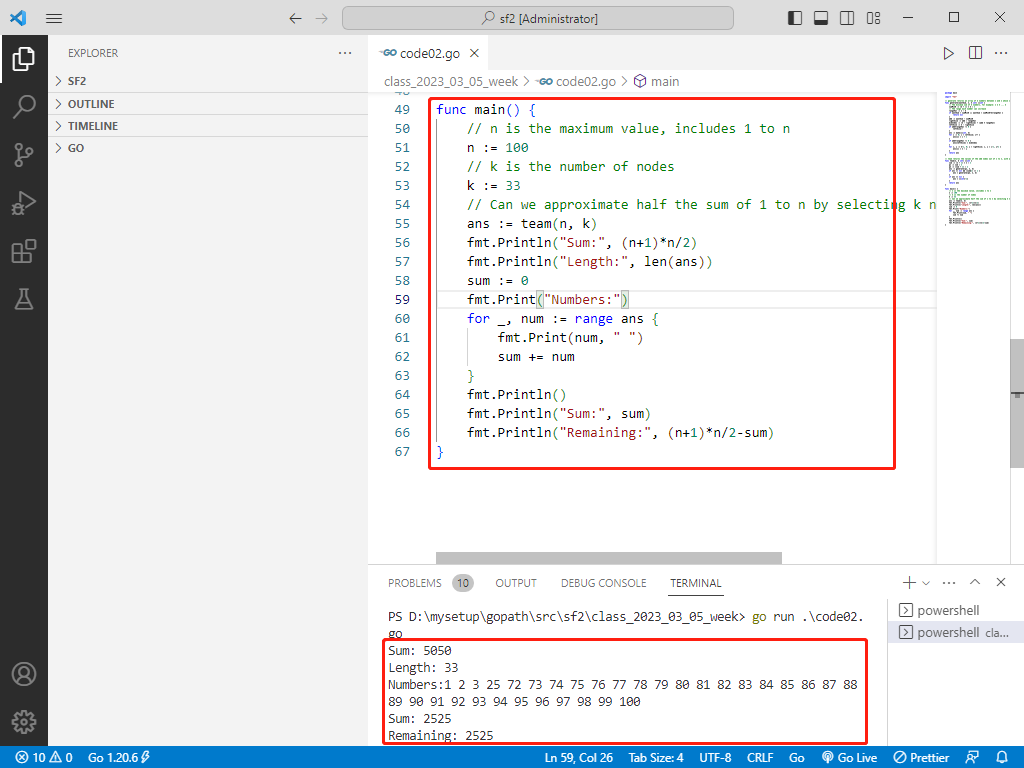
rust完整代码如下:
fn team(n: i32, k: i32) -> Vec<i32> {
let sum = (n + 1) * n / 2;
let p1 = sum / 2;
let p2 = (sum + 1) / 2;
let ans = generate(p1, n, k);
if ans.is_none() && sum % 2 == 1 {
generate(p2, n, k)
} else {
ans
}
.unwrap_or(vec![-1])
}
fn generate(want_sum: i32, n: i32, k: i32) -> Option<Vec<i32>> {
let sum_min_k = (k + 1) * k / 2;
let range = n - k;
if want_sum < sum_min_k || want_sum > sum_min_k + k * range {
return None;
}
let add = want_sum - sum_min_k;
let right_size = add / range;
let mid_index = (k - right_size) + (add % range);
let left_size = k - right_size - if add % range == 0 { 0 } else { 1 };
let mut ans = vec![0; k as usize];
for i in 0..left_size as usize {
ans[i] = (i + 1) as i32;
}
if add % range != 0 {
ans[left_size as usize] = mid_index;
}
let mut i = k - 1;
let mut j = 0;
while j < right_size {
ans[i as usize] = n - j;
i -= 1;
j += 1;
}
Some(ans)
}
fn main() {
let n = 100;
let k = 33;
let ans = team(n, k);
let sum: i32 = ans.iter().sum();
println!("总和: {}", (n + 1) * n / 2);
println!("长度: {}", ans.len());
print!("数字: ");
for num in ans {
print!("{} ", num);
}
println!();
println!("求和: {}", sum);
println!("剩余: {}", (n + 1) * n / 2 - sum);
}
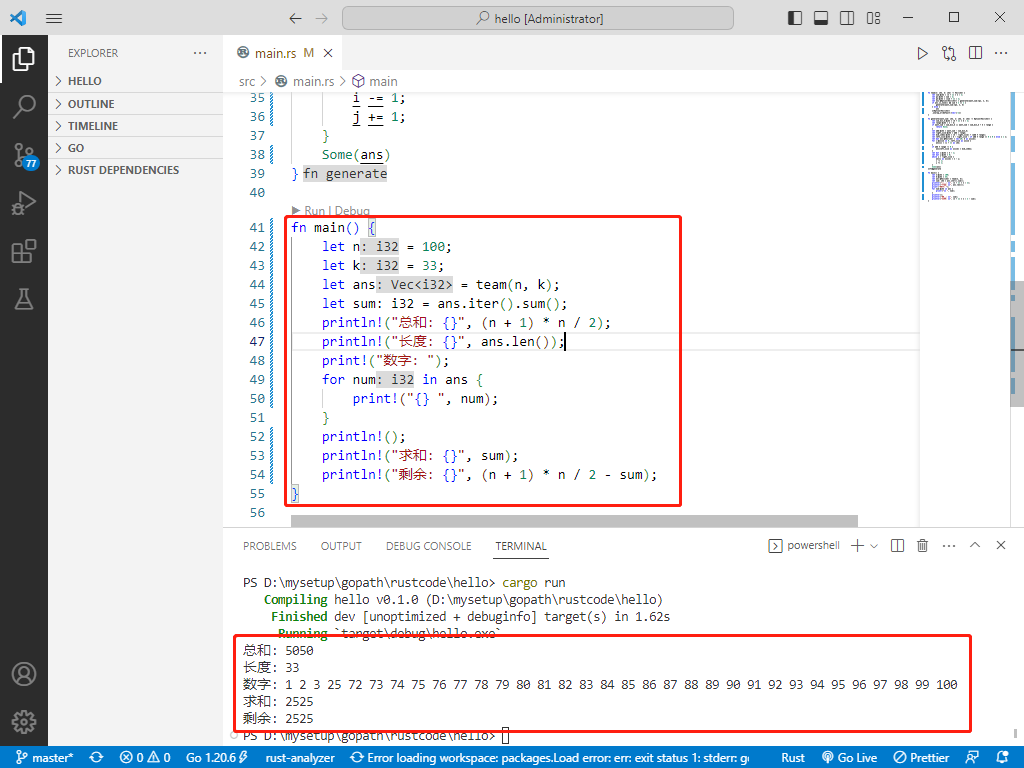
c++完整代码如下:
#include <iostream>
#include <vector>
using namespace std;
vector<int> generate(int wantSum, int n, int k) {
int sumMinK = (k + 1) * k / 2;
int range = n - k;
if (wantSum < sumMinK || wantSum > sumMinK + k * range) {
return {};
}
int add = wantSum - sumMinK;
int rightSize = add / range;
int midIndex = (k - rightSize) + (add % range);
int leftSize = k - rightSize - ((add % range) == 0 ? 0 : 1);
vector<int> ans(k);
for (int i = 0; i < leftSize; i++) {
ans[i] = i + 1;
}
if (add % range != 0) {
ans[leftSize] = midIndex;
}
for (int i = k - 1, j = 0; j < rightSize; i--, j++) {
ans[i] = n - j;
}
return ans;
}
vector<int> team(int n, int k) {
int sum = (n + 1) * n / 2;
int p1 = sum / 2;
int p2 = (sum + 1) / 2;
vector<int> ans = generate(p1, n, k);
if (ans.empty() && (sum & 1) == 1) {
ans = generate(p2, n, k);
}
return ans.empty() ? vector<int>{-1} : ans;
}
int main() {
int n = 100;
int k = 33;
vector<int> ans = team(n, k);
cout << "总和 : " << (n + 1) * n / 2 << endl;
cout << "长度 : " << ans.size() << endl;
int sum = 0;
cout << "数字 : ";
for (int num : ans) {
cout << num << " ";
sum += num;
}
cout << endl;
cout << "求和 : " << sum << endl;
cout << "剩余 : " << ((n + 1) * n / 2 - sum) << endl;
return 0;
}
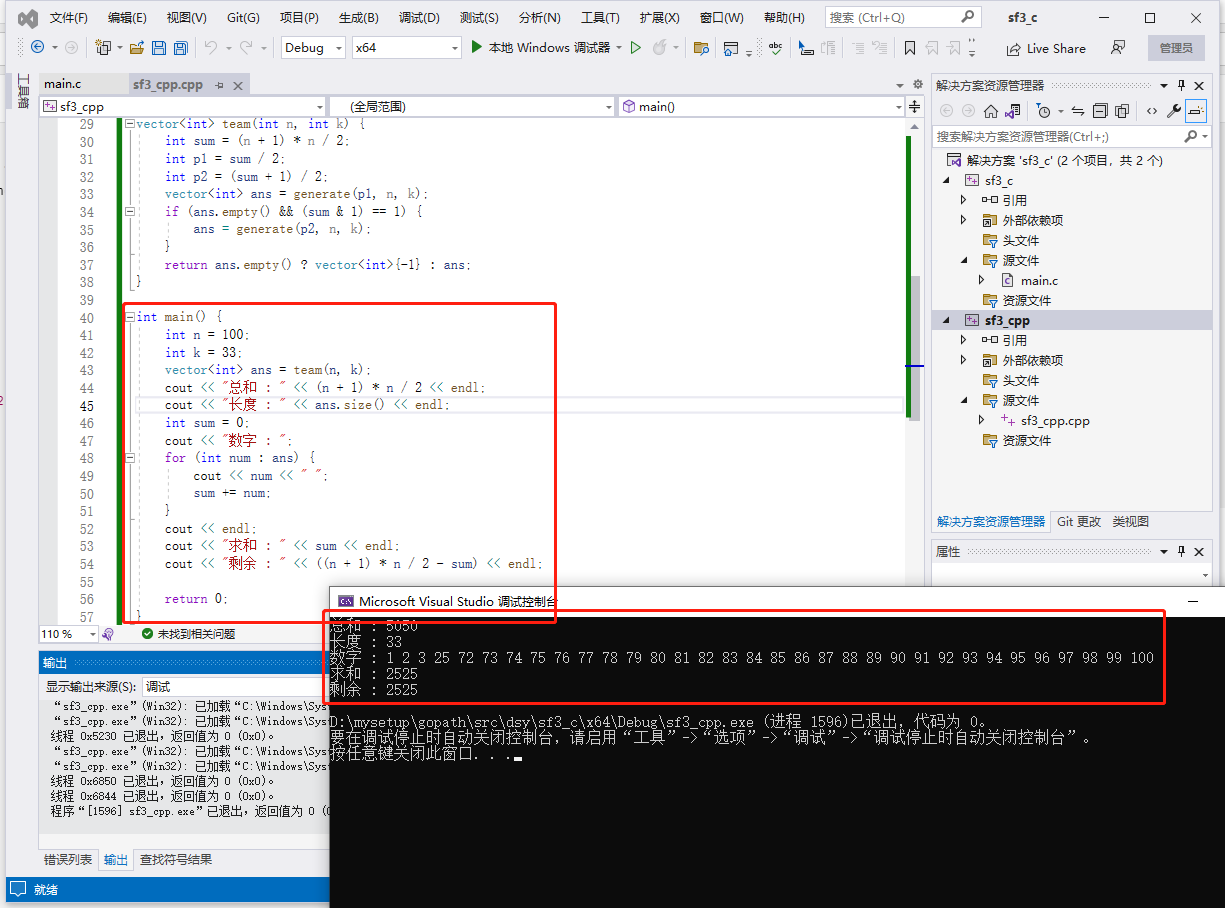
c完整代码如下:
#include <stdio.h>
#include <stdlib.h>
// 一共 1 ~ n 这些数字
// 其中选k个数字
// 一定要让k个数字的累加和是wantSum
// 返回,哪k个数字,只要返回一种方法就可以
int* generate(int wantSum, int n, int k) {
// k个数字,和最小的情况,1 2 3 ... k
int sumMinK = (k + 1) * k / 2;
// 每个数提升的幅度
int range = n - k;
if (wantSum < sumMinK || wantSum > sumMinK + k * range) {
return NULL;
}
int add = wantSum - sumMinK;
int rightSize = add / range;
int midIndex = (k - rightSize) + (add % range);
int leftSize = k - rightSize - (add % range == 0 ? 0 : 1);
int* ans = (int*)malloc(k * sizeof(int));
for (int i = 0; i < leftSize; i++) {
ans[i] = i + 1;
}
if (add % range != 0) {
ans[leftSize] = midIndex;
}
for (int i = k - 1, j = 0; j < rightSize; i--, j++) {
ans[i] = n - j;
}
return ans;
}
// 1 ~ n 奇数节点的个数是k个
// 返回奇数节点的值有哪些
int* team(int n, int k) {
// 1 ~ n , sum = 10 k个奇数 5
// 1 ~ n , sum = 15 k个奇数 7 8
int sum = (n + 1) * n / 2;
int p1 = sum / 2;
int p2 = (sum + 1) / 2;
int* ans = generate(p1, n, k);
if (ans == NULL && (sum & 1) == 1) {
ans = generate(p2, n, k);
}
return ans != NULL ? ans : NULL;
}
int main() {
// n是最大值,1~n这些数字都有
int n = 100;
// k是个数
int k = 33;
// 1~n这些数字,选k个,能不能求和逼近一半
// 返回方案
int* ans = team(n, k);
if (ans != NULL) {
printf("总和 : %d\n", (n + 1) * n / 2);
printf("长度 : %d\n", k);
int sum = 0;
printf("数字 : ");
for (int i = 0; i < k; i++) {
printf("%d ", ans[i]);
sum += ans[i];
}
printf("\n");
printf("求和 : %d\n", sum);
printf("剩余 : %d\n", ((n + 1) * n / 2 - sum));
}
else {
printf("无解\n");
}
free(ans); // 释放内存
return 0;
}
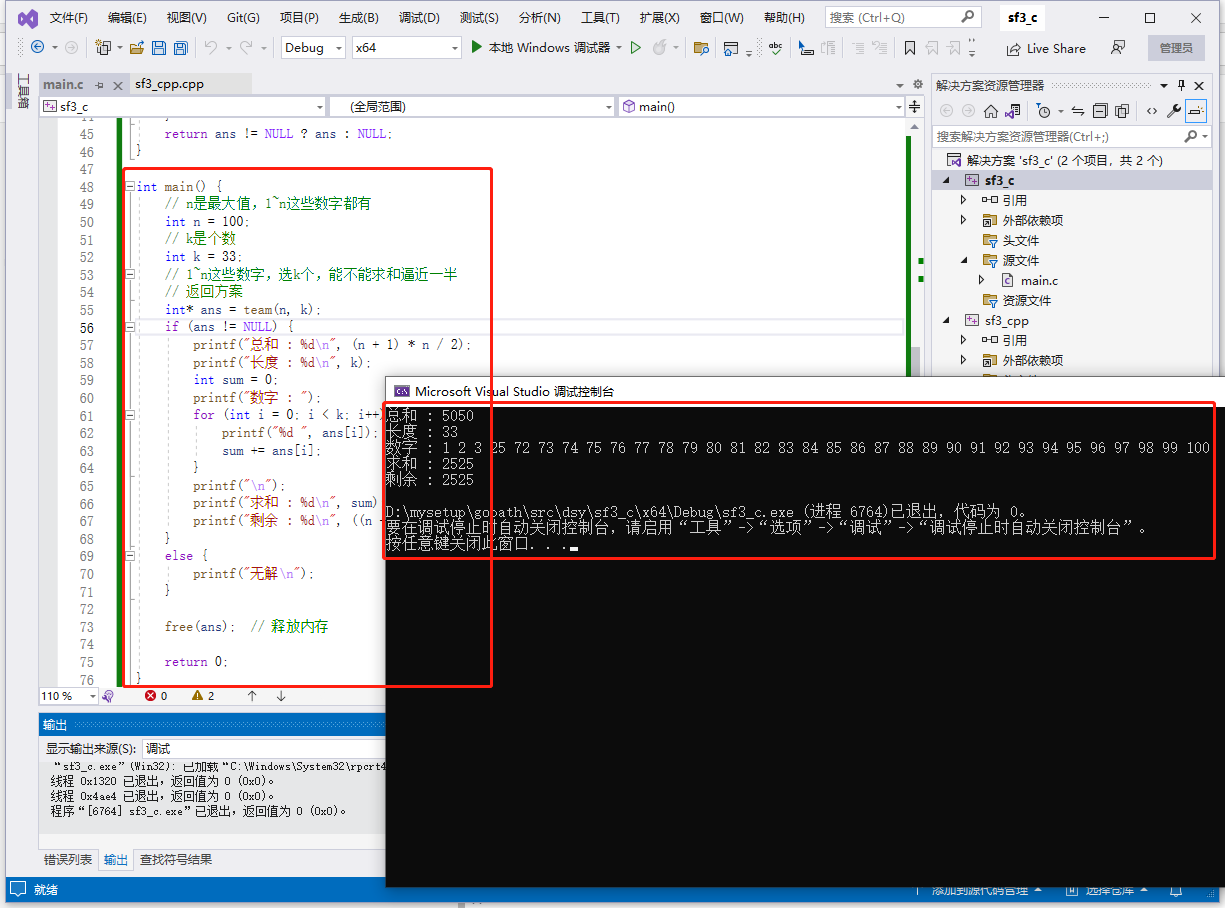
公众号:福大大架构师每日一题



 浙公网安备 33010602011771号
浙公网安备 33010602011771号