2023-07-25:你驾驶出租车行驶在一条有 n 个地点的路上 这 n 个地点从近到远编号为 1 到 n ,你想要从 1 开到 n 通过接乘客订单盈利。你只能沿着编号递增的方向前进,不能改变方向 乘
2023-07-25:你驾驶出租车行驶在一条有 n 个地点的路上
这 n 个地点从近到远编号为 1 到 n ,你想要从 1 开到 n
通过接乘客订单盈利。你只能沿着编号递增的方向前进,不能改变方向
乘客信息用一个下标从 0 开始的二维数组 rides 表示
其中 rides[i] = [starti, endi, tipi]
表示第 i 位乘客需要从地点 starti 前往 endi
愿意支付 tipi 元的小费
每一位 你选择接单的乘客 i ,你可以 盈利 endi - starti + tipi 元
你同时 最多 只能接一个订单。
给你 n 和 rides ,请你返回在最优接单方案下,你能盈利 最多 多少元。
注意:你可以在一个地点放下一位乘客,并在同一个地点接上另一位乘客。
输入:n = 5, rides = [[2,5,4],[1,5,1]]。
输出:7。
答案2023-07-25:
maxTaxiEarnings1算法的大体过程如下:
1.对乘客订单rides按照起始地点的编号进行升序排序。
2.调用build函数,构建区间树数据结构,初始化max数组。
3.遍历排序后的rides数组,对每个乘客订单进行处理:
a.根据乘客订单的起始地点,通过maxQuery函数查询当前位置之前的最大盈利额,存储在money变量中。
b.计算当前乘客订单的盈利额,即end-start+tip。
c.将当前乘客订单的结束地点作为索引,更新max数组中对应位置的值,更新为money+当前乘客订单的盈利额。
4.返回maxQuery函数查询整个路程的最大盈利额,即maxQuery(n)。
maxTaxiEarnings2算法的大体过程如下:
1.初始化sorted数组,用于存储所有乘客订单的起始和结束地点,长度为乘客订单数量的两倍。
2.遍历rides数组,将乘客订单的起始和结束地点依次存储到sorted数组中。
3.对sorted数组进行升序排序。
4.对乘客订单rides按照起始地点的编号进行升序排序。
5.初始化dp数组,并将所有元素置为0。
6.初始化dpi变量为0,用于记录当前处理到的sorted数组下标。
7.初始化pre和ans变量为0。
8.遍历排序后的rides数组,对每个乘客订单进行处理:
a.获取当前乘客订单的起始和结束地点。
b.分别使用rank函数查找sorted数组中起始和结束地点的下标。
c.更新dp数组,从dpi到起始地点的下标之间的元素,将其值更新为max(pre, dp[dpi])。
d.计算当前乘客订单的盈利额,即end-start+tip。
e.更新ans变量,取盈利额和当前ans的最大值。
f.将dp数组中结束地点的下标位置的值更新为max(dp[erank], 盈利额)。
9.返回ans变量,即最大盈利额。
这两种算法的核心思想都是通过动态规划来计算每个乘客订单的盈利额,并利用区间树或排序数组来快速查询之前的最大盈利额,从而得到整个路程的最大盈利额。
maxTaxiEarnings1算法的总的时间复杂度为O(nlogn),总的额外空间复杂度为O(n)。
maxTaxiEarnings2算法的总的时间复杂度为O(nlogn),总的额外空间复杂度为O(n)。
go完整代码如下:
package main
import (
"fmt"
"sort"
)
const MAXN = 100001
var max = make([]int64, MAXN<<2)
var sorted = make([]int, MAXN)
var dp = make([]int64, MAXN)
var n = 0
func build(l, r, rt int) {
if l == r {
max[rt] = 0
} else {
mid := (l + r) / 2
build(l, mid, rt<<1)
build(mid+1, r, rt<<1|1)
pushUp(rt)
}
}
func maxQuery(r int) int64 {
if r < 1 {
return 0
}
return maxQueryRange(1, r, 1, n, 1)
}
func maxQueryRange(L, R, l, r, rt int) int64 {
if L <= l && r <= R {
return max[rt]
}
mid := (l + r) >> 1
ans := int64(0)
if L <= mid {
ans = max64(ans, maxQueryRange(L, R, l, mid, rt<<1))
}
if R > mid {
ans = max64(ans, maxQueryRange(L, R, mid+1, r, rt<<1|1))
}
return ans
}
func update(index int, c int64) {
updateNode(index, c, 1, n, 1)
}
func updateNode(index int, c int64, l, r, rt int) {
if l == r {
max[rt] = max64(max[rt], c)
} else {
mid := (l + r) >> 1
if index <= mid {
updateNode(index, c, l, mid, rt<<1)
} else {
updateNode(index, c, mid+1, r, rt<<1|1)
}
pushUp(rt)
}
}
func pushUp(rt int) {
max[rt] = max64(max[rt<<1], max[rt<<1|1])
}
func maxTaxiEarnings1(len int, rides [][]int) int64 {
sort.Slice(rides, func(i, j int) bool {
return rides[i][0] < rides[j][0]
})
n = len
build(1, n, 1)
for _, ride := range rides {
money := maxQuery(ride[0]) + int64(ride[1]-ride[0]+ride[2])
update(ride[1], money)
}
return maxQuery(n)
}
func rank(sorted []int, len int, num int) int {
ans := 0
l := 0
r := len - 1
for l <= r {
m := (l + r) / 2
if sorted[m] >= num {
ans = m
r = m - 1
} else {
l = m + 1
}
}
return ans
}
func maxTaxiEarnings2(len0 int, rides [][]int) int64 {
m := len(rides)
j := 0
for i := 0; i < m; i++ {
sorted[j] = rides[i][0]
j++
sorted[j] = rides[i][1]
j++
}
sort.Slice(rides, func(i, j int) bool {
return rides[i][0] < rides[j][0]
})
sort.Ints(sorted[:m<<1])
for i := 0; i < m<<1; i++ {
dp[i] = 0
}
dpi := 0
pre := int64(0)
ans := int64(0)
for _, ride := range rides {
start := ride[0]
end := ride[1]
tips := ride[2]
srank := rank(sorted, m<<1, start)
erank := rank(sorted, m<<1, end)
for dpi <= srank {
pre = max64(pre, dp[dpi])
dpi++
}
money := pre + int64(end-start+tips)
ans = max64(money, ans)
dp[erank] = max64(dp[erank], money)
}
return ans
}
func max64(a, b int64) int64 {
if a > b {
return a
}
return b
}
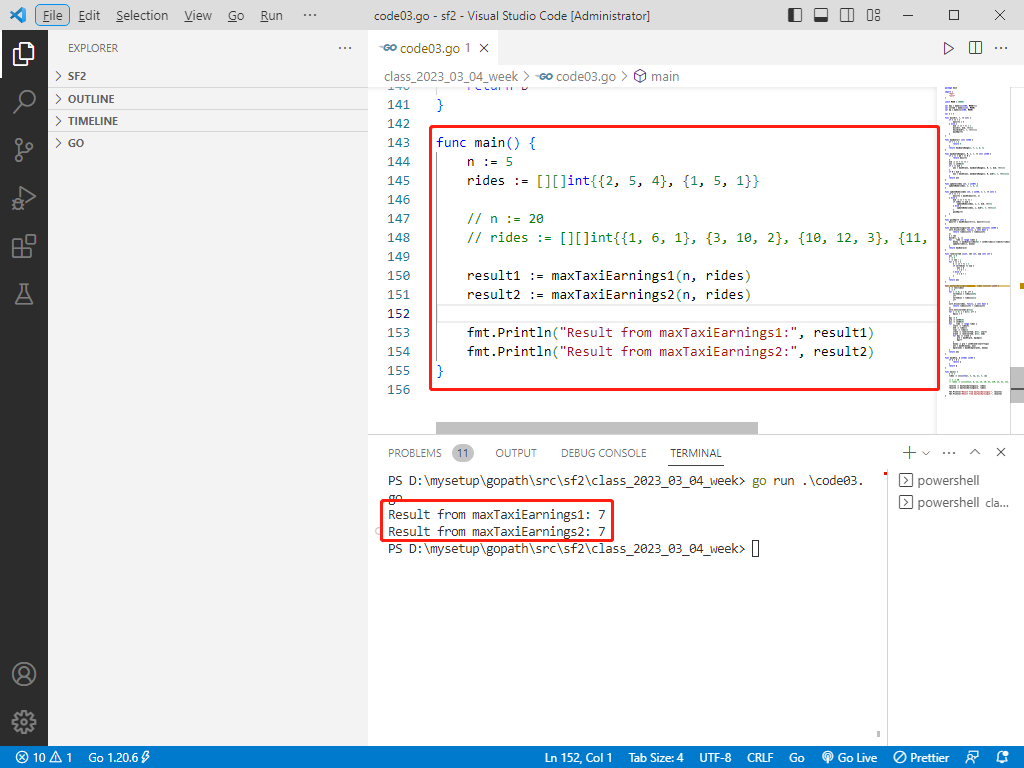
func main() {
n := 5
rides := [][]int{{2, 5, 4}, {1, 5, 1}}
// n := 20
// rides := [][]int{{1, 6, 1}, {3, 10, 2}, {10, 12, 3}, {11, 12, 2}, {12, 15, 2}, {13, 18, 1}}
result1 := maxTaxiEarnings1(n, rides)
result2 := maxTaxiEarnings2(n, rides)
fmt.Println("Result from maxTaxiEarnings1:", result1)
fmt.Println("Result from maxTaxiEarnings2:", result2)
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号