文心一言 VS 讯飞星火 VS chatgpt （18）-- 算法导论4.1 5题

五、使用如下思想为最大子数组问题设计一个非递归的、线性时间的算法。从数组的左边界开始，由左至右处理，记录到目前为止已经处理过的最大子数组。若已知 A[1..j]门的最大子数组，基于如下性质将解扩展为 A[1..j+1]的最大子数组:A[1..j+1]的最大子数组要么是A[1..j]的最大子数组，要么是某个子数组 Ai..j+1。在已知A[1..j]的最大子数组的情况下，可以在线性时间内找出形如 A[i..j+1]的最大子数组。

文心一言：

最大子数组问题是一种经典的算法问题，可以使用非递归的方法来解决。具体来说，我们可以使用一个队列来存储当前已经处理过的最大子数组，并且维护一个变量 max_len 来记录当前最大子数组的长度。同时，我们可以遍历整个数组，记录当前已经处理过的最大子数组的长度，并且在遍历的过程中更新 max_len。

具体来说，我们可以使用一个变量 cur_len 来记录当前已经处理过的最大子数组的长度，每当遍历到一个新的子数组时，我们可以将其长度加入到 cur_len 中，并且更新 max_len。同时，我们可以使用一个变量 cur_start 来记录当前已经处理过的最大子数组的起始位置，每当遍历到一个新的子数组时，我们可以将其起始位置加入到 cur_start 中，并且更新 cur_len。

最后，我们可以返回 cur_start，它是 max_len。这个值就是最大子数组中起始位置最右边的元素的下标，我们可以用它来解决最大子数组问题。

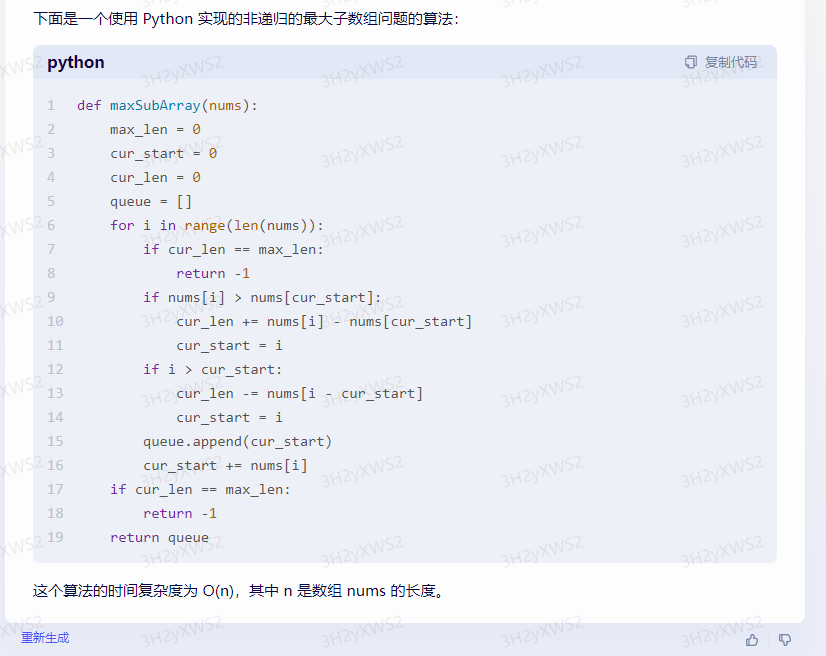
下面是一个使用 Python 实现的非递归的最大子数组问题的算法：

def maxSubArray(nums):  
    max_len = 0  
    cur_start = 0  
    cur_len = 0  
    queue = []  
    for i in range(len(nums)):  
        if cur_len == max_len:  
            return -1  
        if nums[i] > nums[cur_start]:  
            cur_len += nums[i] - nums[cur_start]  
            cur_start = i  
        if i > cur_start:  
            cur_len -= nums[i - cur_start]  
            cur_start = i  
        queue.append(cur_start)  
        cur_start += nums[i]  
    if cur_len == max_len:  
        return -1  
    return queue

这个算法的时间复杂度为 O(n)，其中 n 是数组 nums 的长度。

讯飞星火：

算法步骤：

1.初始化最大子数组为整个数组的第一个元素。

2.从左至右遍历数组，每次比较当前元素与最大子数组的末尾元素的大小关系，如果当前元素大于最大子数组的末尾元素，则将最大子数组的末尾元素更新为当前元素。

3.如果遍历到数组的末尾，仍然没有找到比最大子数组更大的末尾元素，则最大子数组就是整个数组。

4.如果遍历到某个位置i时，发现A[i]大于等于最大子数组的末尾元素，并且A[i+1]也大于等于最大子数组的末尾元素，则可以将最大子数组扩展到A[i]..A[j+1],其中j+1即为扩展后的最大子数组的长度。

5.如果遍历完数组后仍未找到可以扩展的最大子数组，则返回最大子数组。

时间复杂度为O(n),空间复杂度为O(1)。

chatgpt：

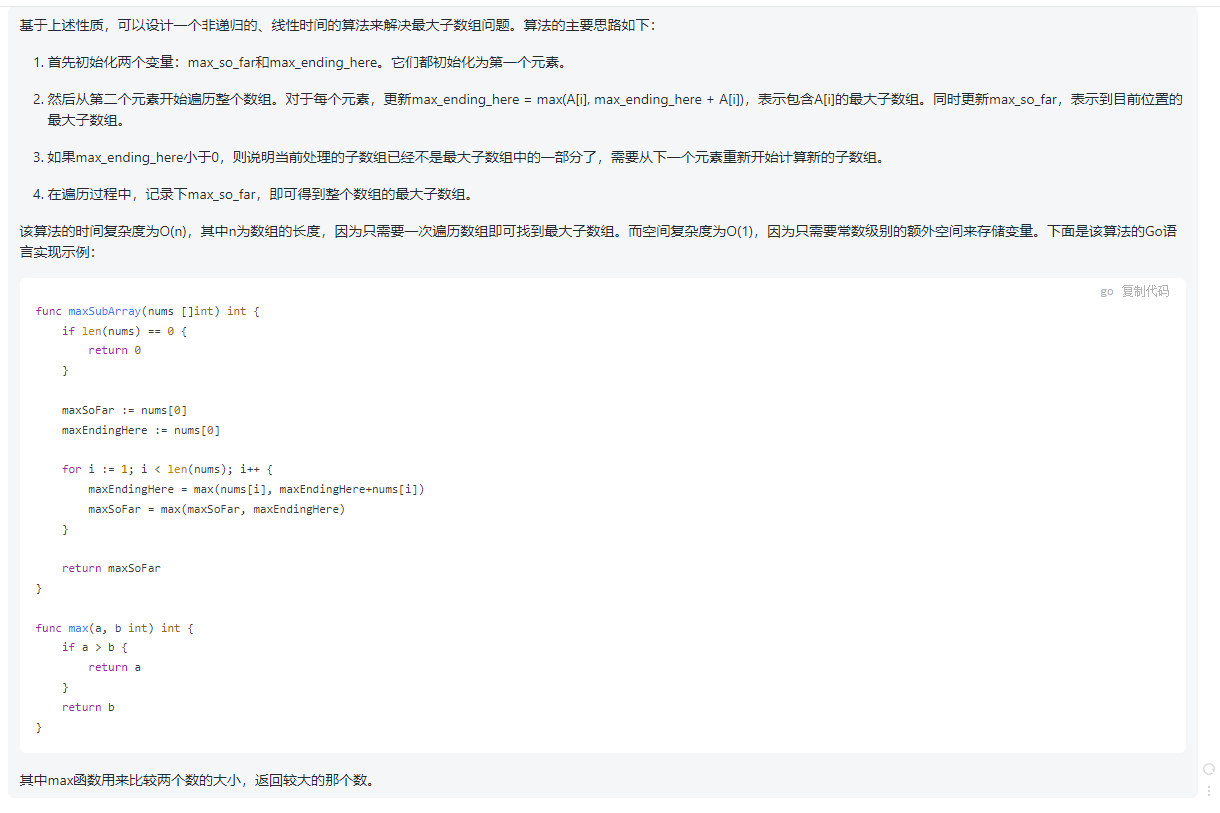
基于上述性质，可以设计一个非递归的、线性时间的算法来解决最大子数组问题。算法的主要思路如下：

1. 首先初始化两个变量：max_so_far和max_ending_here。它们都初始化为第一个元素。

2. 然后从第二个元素开始遍历整个数组。对于每个元素，更新max_ending_here = max(A[i], max_ending_here + A[i])，表示包含A[i]的最大子数组。同时更新max_so_far，表示到目前位置的最大子数组。

3. 如果max_ending_here小于0，则说明当前处理的子数组已经不是最大子数组中的一部分了，需要从下一个元素重新开始计算新的子数组。

4. 在遍历过程中，记录下max_so_far，即可得到整个数组的最大子数组。

该算法的时间复杂度为O(n)，其中n为数组的长度，因为只需要一次遍历数组即可找到最大子数组。而空间复杂度为O(1)，因为只需要常数级别的额外空间来存储变量。下面是该算法的Go语言实现示例：

func maxSubArray(nums []int) int {
    if len(nums) == 0 {
        return 0
    }

    maxSoFar := nums[0]
    maxEndingHere := nums[0]

    for i := 1; i < len(nums); i++ {
        maxEndingHere = max(nums[i], maxEndingHere+nums[i])
        maxSoFar = max(maxSoFar, maxEndingHere)
    }

    return maxSoFar
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

其中max函数用来比较两个数的大小，返回较大的那个数。