2023-05-18:有 n 名工人。 给定两个数组 quality 和 wage , 其中,quality[i] 表示第 i 名工人的工作质量,其最低期望工资为 wage[i] 。 现在我们想雇佣
2023-05-18:有 n 名工人。 给定两个数组 quality 和 wage ,
其中,quality[i] 表示第 i 名工人的工作质量,其最低期望工资为 wage[i] 。
现在我们想雇佣 k 名工人组成一个工资组。在雇佣 一组 k 名工人时,
我们必须按照下述规则向他们支付工资:
对工资组中的每名工人,应当按其工作质量与同组其他工人的工作质量的比例来支付工资。
工资组中的每名工人至少应当得到他们的最低期望工资。
给定整数 k ,返回 组成满足上述条件的付费群体所需的最小金额。
输入: quality = [10,20,5], wage = [70,50,30], k = 2。
输出: 105.00000。
答案2023-05-18:
解题步骤:
1.构造 Employee 结构体,存储每个员工的工作质量和垃圾系数(wage / quality)。
2.按照垃圾系数从小到大对所有员工进行排序。
3.维护一个大小为 k 的小根堆,表示当前最低期望工资组中的 k 名工人的工作质量。
4.遍历所有员工,如果堆未满,则将该员工加入堆中并更新最低期望工资。如果堆已满,则检查当前员工能否替换堆顶元素,如果可以,则弹出堆顶元素并将当前员工入堆,更新最低期望工资。
5.最终返回最低期望工资即可。
注意事项:
-
使用 golang 内置的 container/heap 库来实现小根堆。
-
在比较垃圾系数大小时,需要使用小于等于号,因为可能存在两个员工的垃圾系数完全相等的情况。
时间复杂度:排序所需的时间为 O(nlogn),遍历员工数组时每个员工会入堆一次,出堆一次,即共进行了 2n 次操作,而小根堆的插入和弹出操作时间复杂度均为 O(logk),因此总时间复杂度为 O(nlogn + nlogk)。
空间复杂度:除给定数组外,我们还需要构造 Employee 结构体,以及维护大小为 k 的小根堆,因此需要额外使用 O(n) 空间来存储结构体数组,并且在堆满时可能需要对堆进行调整,最多需要 O(k) 的额外空间。因此总空间复杂度为 O(n + k)。
go完整代码如下:
package main
import (
"container/heap"
"fmt"
"sort"
)
type Employee struct {
RubbishDegree float64
Quality int
}
func NewEmployee(w, q int) Employee {
return Employee{RubbishDegree: float64(w) / float64(q), Quality: q}
}
type EmployeeHeap []int
func (h EmployeeHeap) Len() int { return len(h) }
func (h EmployeeHeap) Less(i, j int) bool { return h[i] > h[j] }
func (h EmployeeHeap) Swap(i, j int) { h[i], h[j] = h[j], h[i] }
func (h *EmployeeHeap) Push(x interface{}) { *h = append(*h, x.(int)) }
func (h *EmployeeHeap) Pop() interface{} {
n := len(*h)
x := (*h)[n-1]
*h = (*h)[:n-1]
return x
}
func min(a, b float64) float64 {
if a < b {
return a
}
return b
}
func mincostToHireWorkers(quality []int, wage []int, k int) float64 {
n := len(quality)
employees := make([]Employee, n)
for i := range quality {
employees[i] = NewEmployee(wage[i], quality[i])
}
sort.Slice(employees, func(i, j int) bool {
return employees[i].RubbishDegree <= employees[j].RubbishDegree
})
minTops := &EmployeeHeap{}
heap.Init(minTops)
ans, qualitySum := 1e9, 0
for i := 0; i < n; i++ {
curQuality := employees[i].Quality
if minTops.Len() < k { // 堆没满
qualitySum += curQuality
heap.Push(minTops, curQuality)
if minTops.Len() == k {
ans = min(ans, float64(qualitySum)*employees[i].RubbishDegree)
}
} else { // 来到当前员工的时候,堆是满的!
// 当前员工的能力,可以把堆顶干掉,自己进来!
if top := (*minTops)[0]; top > curQuality {
heap.Pop(minTops)
qualitySum += curQuality - top
heap.Push(minTops, curQuality)
ans = min(ans, float64(qualitySum)*employees[i].RubbishDegree)
}
}
}
return ans
}
func main() {
quality := []int{10, 20, 5}
wage := []int{70, 50, 30}
k := 2
result := mincostToHireWorkers(quality, wage, k)
fmt.Println(result)
}
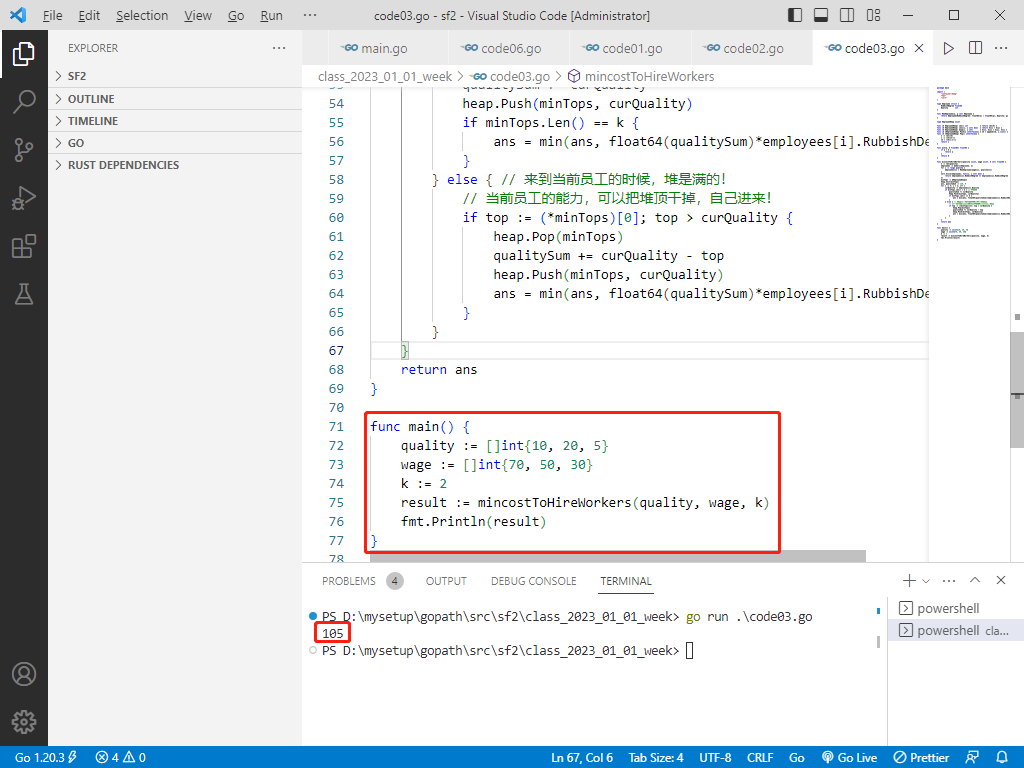
rust完整代码如下:
struct Employee {
rubbish_degree: f64,
quality: i32,
}
impl Employee {
fn new(w: i32, q: i32) -> Self {
let rubbish_degree = w as f64 / q as f64;
Self {
rubbish_degree,
quality: q,
}
}
}
fn mincost_to_hire_workers(quality: Vec<i32>, wage: Vec<i32>, k: i32) -> f64 {
let n = quality.len();
let mut employees = Vec::with_capacity(n);
for i in 0..n {
employees.push(Employee::new(wage[i], quality[i]));
}
// 只根据垃圾指数排序
// 要价 / 能力
employees.sort_by(|a, b| a.rubbish_degree.partial_cmp(&b.rubbish_degree).unwrap());
// 请维持力量最小的前K个力量
// 大根堆!门槛堆!
let mut min_tops = std::collections::BinaryHeap::new();
let mut ans = std::f64::MAX;
let mut quality_sum = 0;
for i in 0..n {
// i : 依次所有员工的下标
// quality_sum : 进入堆的力量总和!
// cur_quality当前能力
let cur_quality = employees[i].quality;
if min_tops.len() < k as usize {
// 堆没满
quality_sum += cur_quality;
min_tops.push(cur_quality);
if min_tops.len() == k as usize {
ans = ans.min(quality_sum as f64 * employees[i].rubbish_degree);
}
} else {
// 来到当前员工的时候,堆是满的!
// 当前员工的能力,可以把堆顶干掉,自己进来!
if let Some(top) = min_tops.peek() {
if *top > cur_quality {
quality_sum += cur_quality - min_tops.pop().unwrap();
min_tops.push(cur_quality);
ans = ans.min(quality_sum as f64 * employees[i].rubbish_degree);
}
}
}
}
ans
}
fn main() {
let quality = vec![10, 20, 5];
let wage = vec![70, 50, 30];
let k = 2;
let result = mincost_to_hire_workers(quality, wage, k);
println!("{}", result);
}
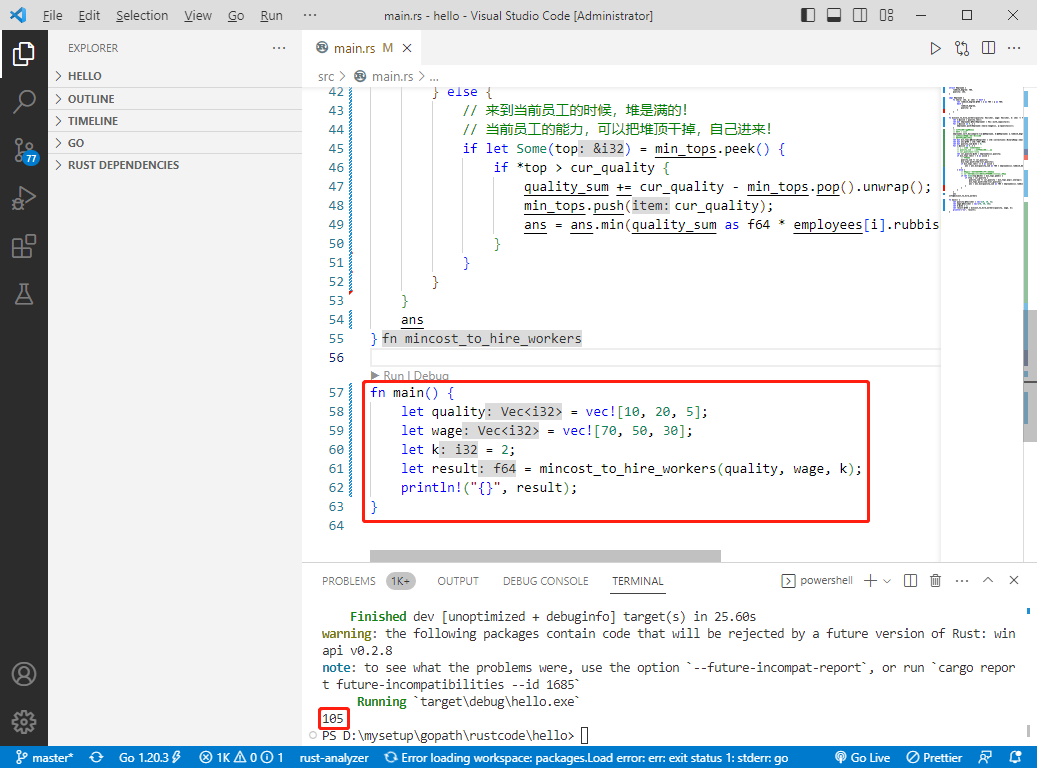
c完整代码如下:
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
typedef struct Employee {
double rubbishDegree;
int quality;
} Employee;
int cmp(const void* a, const void* b) {
Employee* pa = (Employee*)a;
Employee* pb = (Employee*)b;
if (pa->rubbishDegree < pb->rubbishDegree) {
return -1;
}
else if (pa->rubbishDegree > pb->rubbishDegree) {
return 1;
}
else {
return 0;
}
}
double mincostToHireWorkers(int* quality, int qualitySize, int* wage, int wageSize, int k) {
int n = qualitySize;
Employee* employees = (Employee*)malloc(n * sizeof(Employee));
for (int i = 0; i < n; i++) {
employees[i].quality = quality[i];
employees[i].rubbishDegree = (double)wage[i] / (double)quality[i];
}
qsort(employees, n, sizeof(Employee), cmp);
int* minTops = (int*)malloc(k * sizeof(int));
int topIndex = -1;
double ans = INT_MAX;
int qualitySum = 0;
for (int i = 0; i < n; i++) {
int curQuality = employees[i].quality;
if (topIndex < k - 1) {
qualitySum += curQuality;
minTops[++topIndex] = curQuality;
if (topIndex == k - 1) {
ans = qualitySum * employees[i].rubbishDegree;
}
}
else {
if (minTops[0] > curQuality) {
qualitySum += curQuality - minTops[0];
minTops[0] = curQuality;
ans = qualitySum * employees[i].rubbishDegree;
// 调整,使堆继续保持最小堆的性质
for (int j = 0; j < k - 1; j++) {
if (minTops[j] > minTops[j + 1]) {
int tmp = minTops[j];
minTops[j] = minTops[j + 1];
minTops[j + 1] = tmp;
}
else {
break;
}
}
}
}
}
free(employees);
free(minTops);
return ans;
}
int main() {
int quality[] = { 10,20,5 };
int wage[] = { 70,50,30 };
int k = 2;
double result = mincostToHireWorkers(quality, sizeof(quality) / sizeof(int), wage, sizeof(wage) / sizeof(int), k);
printf("%lf\n", result);
return 0;
}
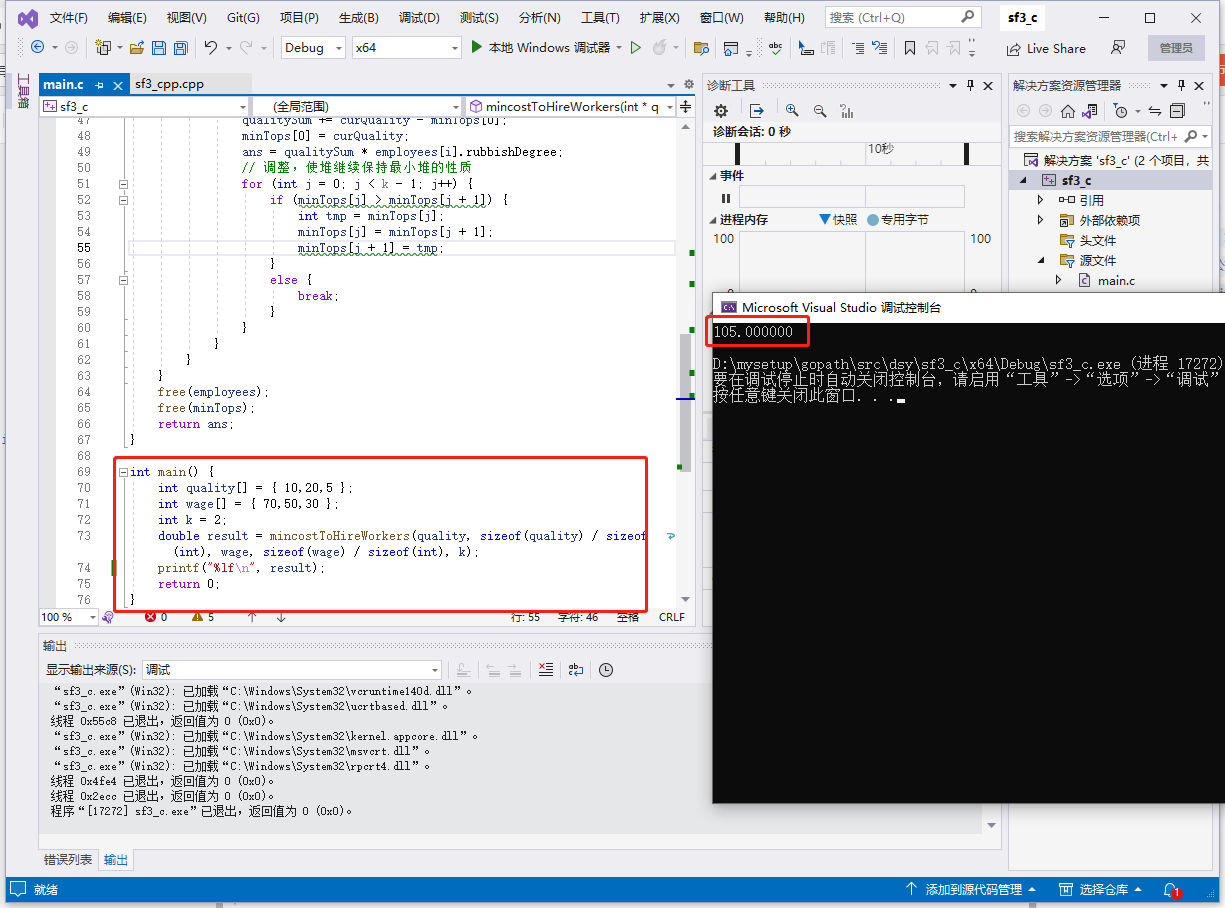
c++完整代码如下:
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
#include <limits>
using namespace std;
struct Employee {
double rubbishDegree;
int quality;
Employee() = default;
Employee(int w, int q) : rubbishDegree(static_cast<double>(w) / static_cast<double>(q)), quality(q) {}
bool operator<(const Employee& other) const {
return rubbishDegree < other.rubbishDegree;
}
};
double mincostToHireWorkers(vector<int>& quality, vector<int>& wage, int k) {
int n = quality.size();
vector<Employee> employees(n);
for (int i = 0; i < n; i++) {
employees[i] = Employee(wage[i], quality[i]);
}
// 只根据垃圾指数排序
sort(employees.begin(), employees.end());
// 请维持力量最小的前K个力量
// 大根堆!门槛堆!
priority_queue<int> minTops;
double ans = numeric_limits<double>::max();
for (int i = 0, qualitySum = 0; i < n; i++) {
// i : 依次所有员工的下标
// qualitySum : 进入堆的力量总和!
// curQuality当前能力
int curQuality = employees[i].quality;
if (minTops.size() < k) { // 堆没满
qualitySum += curQuality;
minTops.push(curQuality);
if (minTops.size() == k) {
ans = min(ans, qualitySum * employees[i].rubbishDegree);
}
}
else { // 来到当前员工的时候,堆是满的!
// 当前员工的能力,可以把堆顶干掉,自己进来!
if (minTops.top() > curQuality) {
// qualitySum -= minTops.top();
// qualitySum += curQuality;
// minTops.pop();
// minTops.push(curQuality);
qualitySum += curQuality - minTops.top();
minTops.pop();
minTops.push(curQuality);
ans = min(ans, qualitySum * employees[i].rubbishDegree);
}
}
}
return ans;
}
int main() {
vector<int> quality = { 10, 20, 5 };
vector<int> wage = { 70, 50, 30 };
int k = 2;
double result = mincostToHireWorkers(quality, wage, k);
cout << result << endl; // 105
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号