2023-05-16:给你一个 严格升序排列 的正整数数组 arr 和一个整数 k 。 请你找到这个数组里第 k 个缺失的正整数。 输入:arr = [2,3,4,7,11], k = 5。 输出:9
2023-05-16:给你一个 严格升序排列 的正整数数组 arr 和一个整数 k 。
请你找到这个数组里第 k 个缺失的正整数。
输入:arr = [2,3,4,7,11], k = 5。
输出:9。
答案2023-05-16:
大体步骤如下:
1.初始化左指针l为0,右指针r为数组长度减一,定义中间指针m和find(找到第k个正整数前的下标位置),并将find初始化为数组长度。
2.当左指针小于等于右指针时,执行二分查找。令m等于左指针和右指针之间的中间值。(注:这里取中间值可以使用位运算优化)。
3.如果当前位置arr[m]减去(m+1)大于等于k,说明第k个缺失的正整数在当前位置左侧,更新find为当前位置m,并把右指针r设为m-1,继续二分查找左半部分。
4.如果当前位置arr[m]减去(m+1)小于k,说明第k个缺失的正整数在当前位置右侧,把左指针l设为m+1,继续二分查找右半部分。
5.查找结束后,如果find等于0,说明要找的是第一个缺失的正整数,返回0即可;否则,找到第k个正整数前的一个位置,把这个位置上的元素赋值给preValue,计算从当前位置到第k个正整数的缺失数量under,最终结果就是preValue加上k减去under的值。
6.返回结果。
时间复杂度为O(logn),其中n是数组的长度。因为代码采用了二分查找的算法,每次查找可以将搜索范围缩小一半,所以时间复杂度为O(logn)。
空间复杂度为O(1),因为代码只使用了常数个变量来存储中间结果,与输入数据的规模大小无关。因此,空间复杂度为常数级别。
go完整代码如下:
package main
import "fmt"
func findKthPositive(arr []int, k int) int {
l := 0
r := len(arr) - 1
m := 0
find := len(arr)
for l <= r {
m = (l + r) / 2
if arr[m]-(m+1) >= k {
find = m
r = m - 1
} else {
l = m + 1
}
}
preValue := 0
if find == 0 {
preValue = 0
} else {
preValue = arr[find-1]
}
under := preValue - find
return preValue + (k - under)
}
func main() {
arr := []int{2, 3, 4, 7, 11}
k := 5
result := findKthPositive(arr, k)
fmt.Println(result)
}
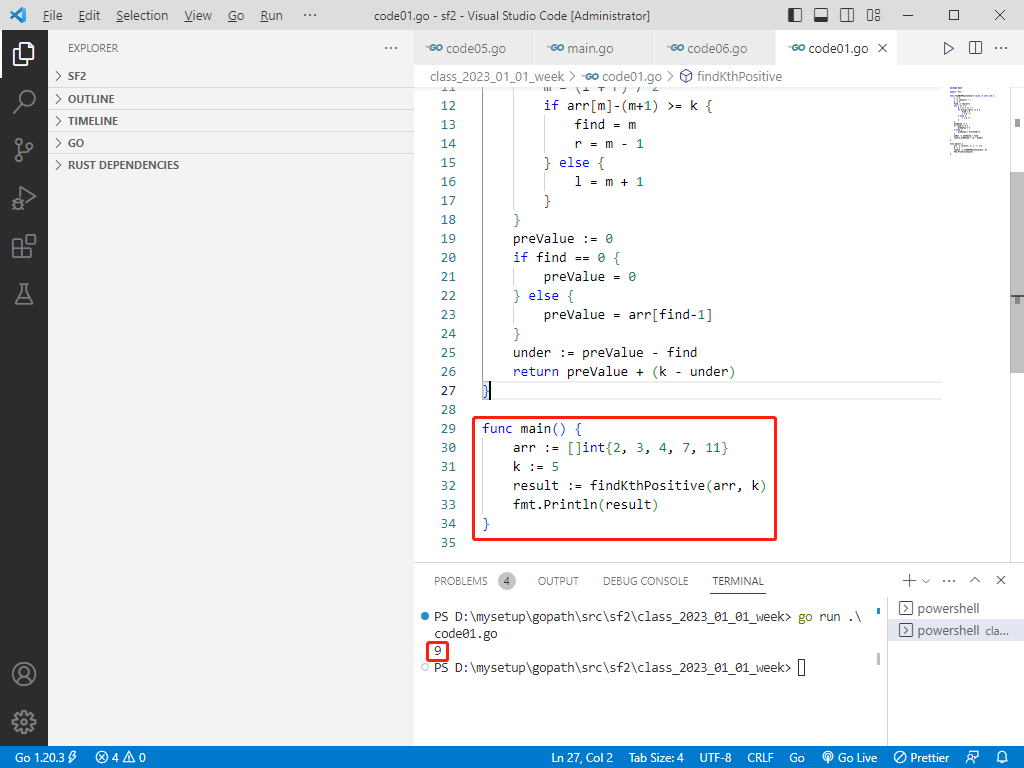
rust完整代码如下:
fn find_kth_positive(arr: Vec<i32>, k: i32) -> i32 {
let mut l = 0;
let mut r = arr.len() - 1;
let mut m = 0;
let mut find = arr.len();
while l <= r {
m = (l + r) / 2;
if arr[m] - (m as i32 + 1) >= k {
find = m;
r = m - 1;
} else {
l = m + 1;
}
}
let pre_value = if find == 0 { 0 } else { arr[find - 1] };
let under = pre_value - (find as i32);
return pre_value + (k - under);
}
fn main() {
let arr: Vec<i32> = vec![2, 3, 4, 7, 11];
let k: i32 = 5;
let result = find_kth_positive(arr, k);
println!("{}", result);
}
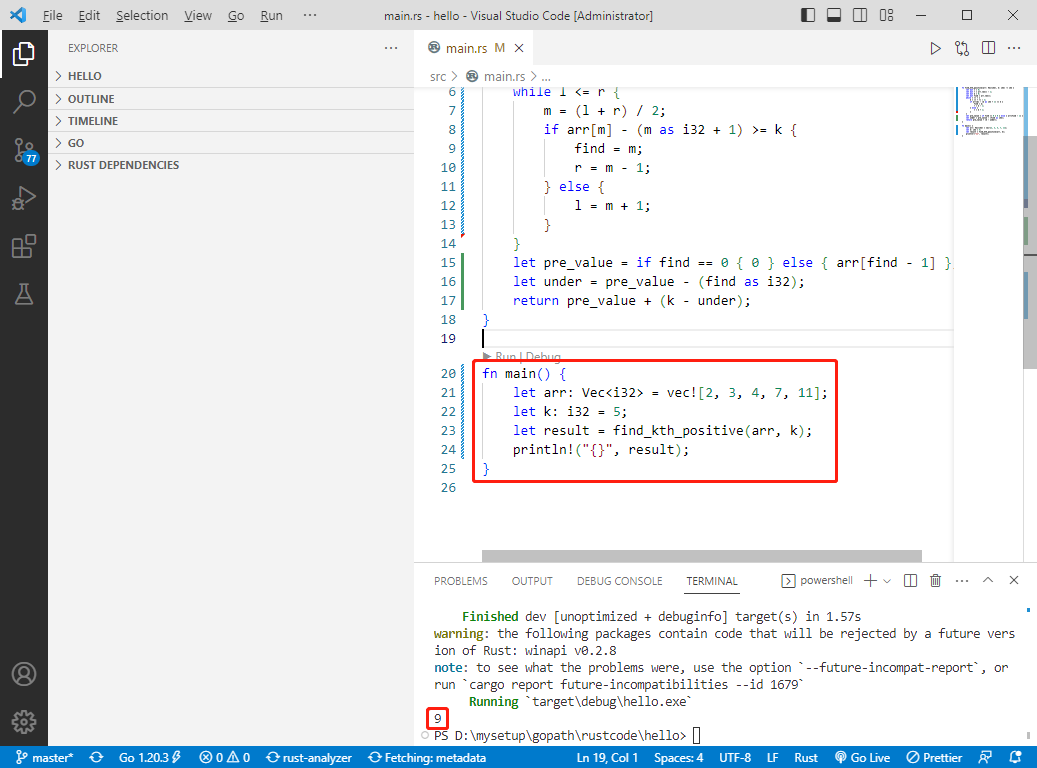
c语言完整代码如下:
#include <stdio.h>
int findKthPositive(int* arr, int arrSize, int k) {
int l = 0;
int r = arrSize - 1;
int m = 0;
int find = arrSize;
while (l <= r) {
m = (l + r) / 2;
if (arr[m] - (m + 1) >= k) {
find = m;
r = m - 1;
}
else {
l = m + 1;
}
}
int preValue = find == 0 ? 0 : arr[find - 1];
int under = preValue - find;
return preValue + (k - under);
}
int main() {
int arr[] = { 2, 3, 4, 7, 11 };
int k = 5;
int arrSize = sizeof(arr) / sizeof(arr[0]);
int result = findKthPositive(arr, arrSize, k);
printf("%d\n", result);
}
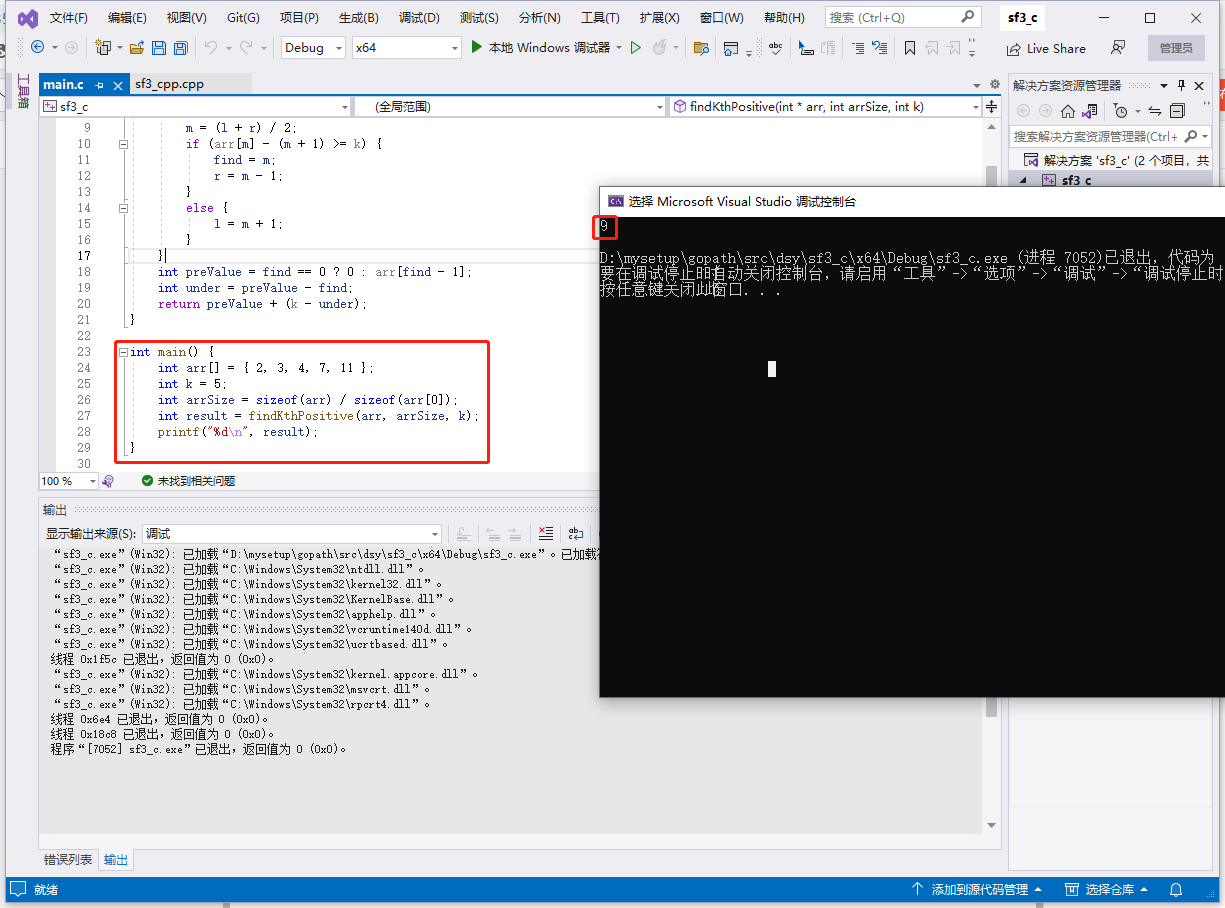
c++完整代码如下:
#include <iostream>
#include <vector>
using namespace std;
int findKthPositive(vector<int>& arr, int k) {
int l = 0;
int r = arr.size() - 1;
int m = 0;
int find = arr.size();
while (l <= r) {
m = (l + r) / 2;
if (arr[m] - (m + 1) >= k) {
find = m;
r = m - 1;
}
else {
l = m + 1;
}
}
int preValue = find == 0 ? 0 : arr[find - 1];
int under = preValue - find;
return preValue + (k - under);
}
int main() {
vector<int> arr = { 2, 3, 4, 7, 11 };
int k = 5;
int result = findKthPositive(arr, k);
cout << result << endl;
}
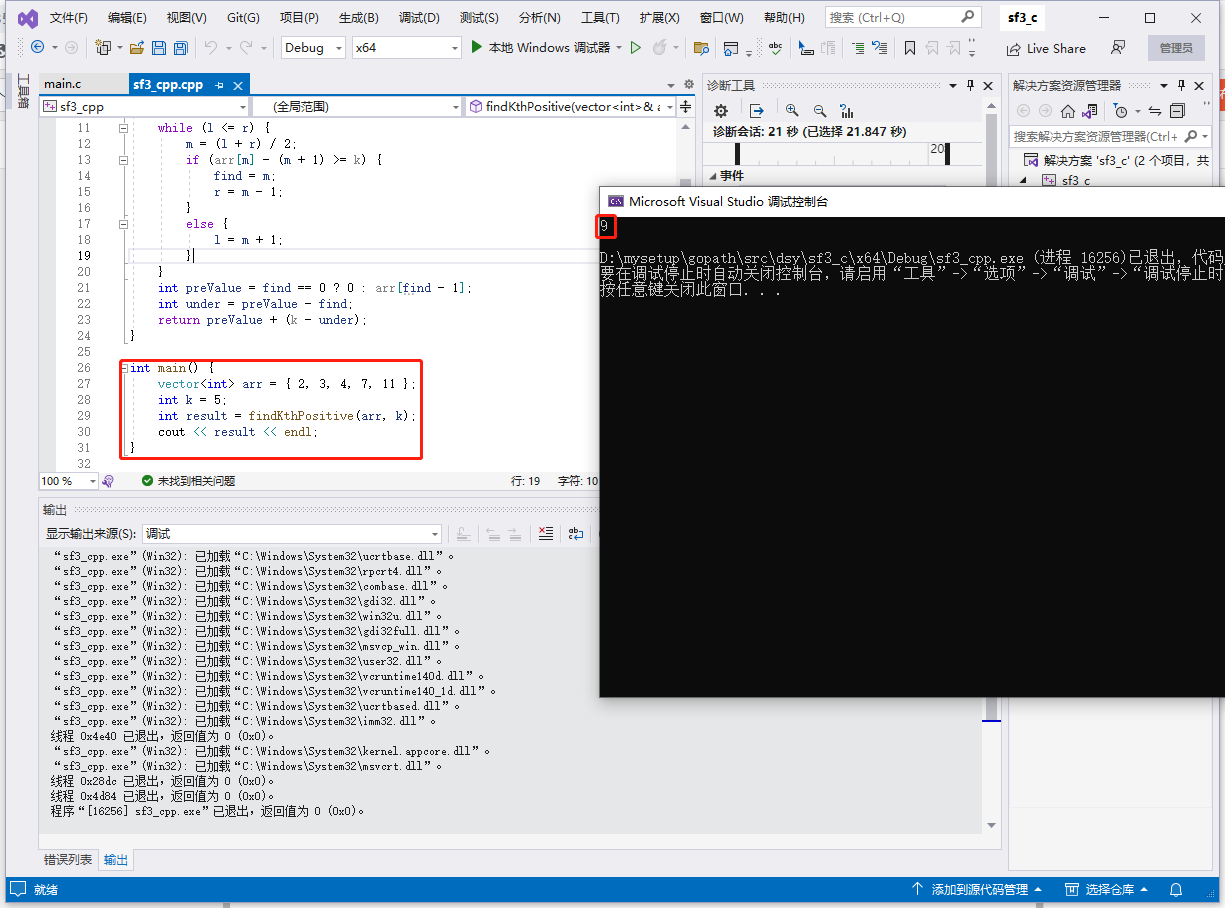
公众号:福大大架构师每日一题



 浙公网安备 33010602011771号
浙公网安备 33010602011771号