2023-03-18:给定一个长度n的数组,每次可以选择一个数x, 让这个数组中所有的x都变成x+1,问你最少的操作次数, 使得这个数组变成一个非降数组。 n <= 3 * 10^5, 0 <= 数值
2023-03-18:给定一个长度n的数组,每次可以选择一个数x,
让这个数组中所有的x都变成x+1,问你最少的操作次数,
使得这个数组变成一个非降数组。
n <= 3 * 10^5,
0 <= 数值 <= 10^9。
来自阿里。
答案2023-03-18:
解题思路
本题可以用多种算法来解决,下面我们将介绍四种常见的做法,分别是暴力枚举、动态规划、单调栈和差分。
方法一:暴力枚举
如果直接对原数组进行修改,那么很容易会导致计算出错或者超时。因此我们可以考虑对数组进行复制,并生成一个布尔型数组op,表示对应位置的元素是否需要进行加1操作。最后,根据op数组来计算最少的加1操作次数。具体实现过程如下:
-
首先找到数组中的最大值max。
-
定义一个长度为max + 1的布尔型数组op,初值全部为false。
-
定义一个递归函数process1,参数分别为op数组、原始数组arr、当前处理到的数字num和max值。该函数的作用是通过遍历op数组,计算经过若干次加1操作后,原始数组是否能够变成一个非降序列,并返回所需的最小操作次数。具体实现过程如下:
-
如果num == max + 1,说明已经遍历完了op数组。此时需要对原数组进行操作,然后判断是否符合非降序列的条件。如果符合,则返回op数组中true值的个数cnt,否则返回std::i32::MAX。
-
否则,在op[num] = true之后调用process1函数,表示将num加1,然后统计所需的操作次数p1。接着,在op[num] = false之后调用process1函数,表示不对num进行任何操作,然后统计所需的操作次数p2。最终返回p1和p2中的最小值。
-
在主函数中,利用rand库生成随机数组,并调用process1函数计算最少的加1操作次数即可。具体实现过程如下:
-
对于功能测试,重复执行test_time次随机实验,并检查计算结果是否正确。
-
对于性能测试,生成长度为n、数值范围为v的随机数组,并重复执行test_time次计算过程,记录总运行时间,并输出平均每次计算的时间。
首先,我们可以通过枚举每一种可能的操作方式,然后依次进行模拟,最后统计最小的操作次数。
假设当前我们已经枚举到了数字x,那么有两种情况:要么对所有等于x的数字进行加1操作,要么不对它们进行加1操作。如此递归下去,直到最终得到一个非降序列。
由于每个数字都只有两种状态(是否进行操作),因此总时间复杂度为O(2^n * n)。当n比较小的时候,这种方法是可行的,但是当n比较大的时候,它会超时。
Rust 代码实现如下:
// 算法1:暴力枚举
fn min_op1(arr: &Vec<i32>) -> i32 {
let max = arr.iter().max().unwrap();
let mut op = vec![false; (*max + 1) as usize];
process1(&mut op, &arr, 0, *max)
}
// 算法1的辅助函数
fn process1(op: &mut Vec<bool>, arr: &Vec<i32>, num: i32, max: i32) -> i32 {
if num == max + 1 {
let mut cnt = 0;
let mut help = vec![0; arr.len()];
for i in 0..arr.len() {
help[i] = arr[i];
}
for i in 0..=max {
if op[i as usize] {
cnt += 1;
add(&mut help, i);
}
}
for i in 1..arr.len() {
if help[i - 1] > help[i] {
return std::i32::MAX;
}
}
return cnt;
} else {
op[num as usize] = true;
let p1 = process1(op, arr, num + 1, max);
op[num as usize] = false;
let p2 = process1(op, arr, num + 1, max);
return p1.min(p2);
}
}
// 算法1的辅助函数,将数组中等于num的元素都加一
fn add(arr: &mut Vec<i32>, num: i32) {
for i in 0..arr.len() {
if arr[i] == num {
arr[i] += 1;
}
}
}
方法二:动态规划
假设最少的加1操作次数为cnt,则有以下结论:
- arr[i] > arr[i + 1]时,必须对arr[i]进行操作,使得arr[i] <= arr[i + 1]。
- 对于所有需要进行操作的数x,我们只需要让它们变成x+1,就能保证数组是非降序列。
因此,可以用动态规划来解决这个问题。具体实现过程如下:
- 如果数组长度小于2,则返回0。
- 定义一个长度为n的数组min,其中min[i]表示arr[i…n-1]中的最小值。
- 定义一个长度为m的布尔型数组add,其中m是数组中的最大值。初始化时全部为false。
- 从左到右遍历数组arr,如果发现arr[i]>min[i+1],则说明必须对arr[i]进行操作,使得arr[i]<=min[i+1]。具体操作是将add[min[i+1]…arr[i]]赋值为true。
- 统计add数组中true值的个数,作为最少的加1操作次数,返回结果即可。
接下来,我们来介绍第二种方法:利用动态规划的思想。具体来说,我们定义一个数组min,其中min[i]表示从i到n-1所需的最小操作次数。那么,如果我们已经知道了min[i+1]的值,我们就可以通过比较arr[i]和min[i+1]来确定是否需要对arr[i]进行操作。如果arr[i]>min[i+1],那么我们需要将所有等于arr[i]的数都进行操作,否则我们不需要对它们进行操作。
这个思路似乎很简单,但还需要考虑一些细节问题。首先,我们需要保证数组中存在至少两个元素,否则显然不需要进行任何操作;其次,我们需要知道整个数组中的最大值max,以便我们可以建立一个辅助bool数组add,其中add[i]表示是否需要对值为i的元素进行操作;最后,我们需要注意一些小细节,例如在比较过程中要使用std::cmp::min函数而不是if else语句等等。
时间复杂度为O(n),空间复杂度也为O(n)。
Rust 代码实现如下:
// 算法2:利用动态规划
fn min_op2(arr: &[i32]) -> i32 {
if arr.len() < 2 {
return 0;
}
let n = arr.len() as i32;
let mut min = vec![0; n as usize];
min[(n - 1) as usize] = arr[(n - 1) as usize];
let mut i = n - 2;
while i >= 0 {
min[i as usize] = std::cmp::min(min[(i + 1) as usize], arr[i as usize]);
i -= 1;
}
let max = *arr.iter().max().unwrap();
let mut add = vec![false; max as usize + 1];
for i in 0..n - 1 {
if arr[i as usize] > min[(i + 1) as usize] {
for j in min[(i + 1) as usize]..arr[i as usize] {
add[j as usize] = true;
}
}
}
add.into_iter().filter(|&is| is).count() as i32
}
方法三:单调栈
单调栈是一个非常有用的数据结构,它可以帮助我们在O(n)的时间复杂度内解决很多问题。对于这道题目,我们可以使用单调栈来求出每个位置需要进行的最小操作次数,然后将所有操作次数相加即可得到答案。具体实现过程如下:
-
定义一个空栈stack和一个长度为n的整型数组res,其中res[i]表示对于位置i,需要进行的最小操作次数。
-
从左到右遍历数组arr,对于每个位置i,执行以下操作:
-
如果stack为空,则将i压入栈中。
-
否则,如果arr[i]>=arr[stack.top()],说明当前位置不需要进行任何操作,直接将i压入栈中。
-
否则,pop出栈顶元素top,并计算res[top] = arr[i]-arr[top]。此时,如果栈为空,则继续将i压入栈中;否则,令j=stack.top(),并重复执行该步骤,直到stack为空或者arr[i]>=arr[j]为止。
-
将res数组中所有元素相加,得到最终的结果。
第三种方法基于单调栈的思想。我们可以维护一个栈,其中存储的是元素下标,同时保持栈中元素的值单调不降。遍历整个数组,对于每个元素,如果它小于栈顶元素,那么就将栈中所有比它大的元素弹出,并且将这些位置对应的add数组设为true。最后,我们只需要统计add数组中为true的元素的个数即可。
时间复杂度为O(n),空间复杂度为O(n)。
Rust 代码实现如下:
// 算法3:利用单调栈
fn min_op3(arr: &[i32]) -> i32 {
let n = arr.len();
let mut m = 0;
for num in arr.iter() {
m = m.max(*num);
}
let mut dst = DynamicSegmentTree::new(m);
let mut max = arr[0];
for i in 1..n {
if max > arr[i] {
dst.set(arr[i], max - 1);
}
max = max.max(arr[i]);
}
dst.sum()
}
struct Node {
sum: i32,
set: bool,
left: Option<Box<Node>>,
right: Option<Box<Node>>,
}
impl Node {
fn new() -> Self {
Node {
sum: 0,
set: false,
left: None,
right: None,
}
}
fn push_down(&mut self, ln: i32, rn: i32) {
if self.left.is_none() {
self.left = Some(Box::new(Node::new()));
}
if self.right.is_none() {
self.right = Some(Box::new(Node::new()));
}
if self.set {
self.left.as_mut().unwrap().set = true;
self.right.as_mut().unwrap().set = true;
self.left.as_mut().unwrap().sum = ln;
self.right.as_mut().unwrap().sum = rn;
self.set = false;
}
}
}
struct DynamicSegmentTree {
root: Node,
size: i32,
}
impl DynamicSegmentTree {
fn new(max: i32) -> Self {
let root = Node::new();
DynamicSegmentTree { root, size: max }
}
fn set(&mut self, s: i32, e: i32) {
Self::update(&mut self.root, 0, self.size, s, e);
}
fn update(c: &mut Node, l: i32, r: i32, s: i32, e: i32) {
if s <= l && r <= e {
c.set = true;
c.sum = r - l + 1;
} else {
let mid = (l + r) >> 1;
c.push_down(mid - l + 1, r - mid);
if s <= mid {
if c.left.is_none() {
c.left = Some(Box::new(Node::new()));
}
DynamicSegmentTree::update(c.left.as_mut().unwrap(), l, mid, s, e);
}
if e > mid {
if c.right.is_none() {
c.right = Some(Box::new(Node::new()));
}
DynamicSegmentTree::update(c.right.as_mut().unwrap(), mid + 1, r, s, e);
}
c.sum = c.left.as_ref().unwrap().sum + c.right.as_ref().unwrap().sum;
}
}
fn sum(&self) -> i32 {
self.root.sum
}
}
方法四:差分
差分数组是一种常用的数据结构,用于快速计算区间修改和区间查询。具体来说,差分数组d[i]表示原数组arr[i]-arr[i-1],即arr[i] = d[1]+d[2]+…+d[i]。因此,如果要将arr[l…r]中的所有元素加上x,只需要将d[l]+=x,同时将d[r+1]-=x即可。最终,通过对差分数组求前缀和,即可得到原数组。对于本题,我们可以先将原数组转化为差分数组,然后利用单调栈来求解最小操作次数。具体实现过程如下:
- 定义一个长度为n的整型数组diff,其中diff[i]=arr[i+1]-arr[i]。
- 利用单调栈来求解diff数组中每个位置需要进行的最小操作次数,具体过程和算法三类似。
- 将所有操作次数相加,得到最终结果。
最后,我们来介绍第四种方法:利用差分数组。我们可以将每个数字看作一个区间,区间的左右端点就是该数字在数组中出现的位置。然后,对于每相邻的两个数字x和y,如果x>y,那么就将区间[y+1, x]中所有数字都加1,表示这些数字需要进行操作。最后,我们只需要统计所有区间的个数即可。
使用差分数组的好处在于它不需要额外的数据结构来辅助计算,而且非常简洁明了。时间复杂度为O(n),空间复杂度为O(n)。
Rust 代码实现如下:
// 算法4:将数组转化为差分数组,统计所有负数的绝对值之和
fn min_op4(arr: &[i32]) -> i32 {
let n = arr.len();
let m = arr.iter().max().unwrap();
unsafe {
for i in 0..CNT {
LCHILD[i] = -1;
RCHILD[i] = -1;
}
CNT = 0;
SUM[CNT] = 0;
SET[CNT] = false;
LEFT[CNT] = 0;
RIGHT[CNT] = *m;
CNT += 1;
let mut max = arr[0];
for i in 1..n {
if max > arr[i] {
set(arr[i], max - 1, 0);
}
max = std::cmp::max(max, arr[i]);
}
sum()
}
}
const MAX_M: usize = 8000000;
static mut SUM: [i32; MAX_M] = [0; MAX_M];
static mut SET: [bool; MAX_M] = [false; MAX_M];
static mut LEFT: [i32; MAX_M] = [0; MAX_M];
static mut RIGHT: [i32; MAX_M] = [0; MAX_M];
static mut LCHILD: [i32; MAX_M] = [-1; MAX_M];
static mut RCHILD: [i32; MAX_M] = [-1; MAX_M];
// 全局初始化函数(需要在安全代码块中使用)
unsafe fn init() {
for i in 0..MAX_M {
LCHILD[i] = -1;
RCHILD[i] = -1;
}
}
static mut CNT: usize = 0;
unsafe fn set(s: i32, e: i32, i: usize) {
let l = LEFT[i];
let r = RIGHT[i];
if s <= l && r <= e {
SET[i] = true;
SUM[i] = r - l + 1;
} else {
let mid = (l + r) >> 1;
down(i, l, mid, mid + 1, r, mid - l + 1, r - mid);
if s <= mid {
set(s, e, LCHILD[i] as usize);
}
if e > mid {
set(s, e, RCHILD[i] as usize);
}
SUM[i] = SUM[LCHILD[i] as usize] + SUM[RCHILD[i] as usize];
}
}
unsafe fn down(i: usize, l1: i32, r1: i32, l2: i32, r2: i32, ln: i32, rn: i32) {
if LCHILD[i] == -1 {
SUM[CNT] = 0;
SET[CNT] = false;
LEFT[CNT] = l1;
RIGHT[CNT] = r1;
LCHILD[i] = CNT as i32;
CNT += 1;
}
if RCHILD[i] == -1 {
SUM[CNT] = 0;
SET[CNT] = false;
LEFT[CNT] = l2;
RIGHT[CNT] = r2;
RCHILD[i] = CNT as i32;
CNT += 1;
}
if SET[i] {
SET[LCHILD[i] as usize] = true;
SET[RCHILD[i] as usize] = true;
SUM[LCHILD[i] as usize] = ln;
SUM[RCHILD[i] as usize] = rn;
SET[i] = false;
}
}
unsafe fn sum() -> i32 {
SUM[0]
}
rust完整代码如下:
use std::time::{Duration, Instant};
// 为了测试
fn main() {
let n = 10usize;
let v = 12;
let test_time = 5000;
println!("功能测试开始");
unsafe {
init(); // 初始化
}
for _ in 0..test_time {
let n = rand::random::<usize>() % n + 1;
let arr = random_array(n, v);
let ans1 = min_op1(&arr); // 算法1
let ans2 = min_op2(&arr); // 算法2
let ans3 = min_op3(&arr); // 算法3
let ans4 = min_op4(&arr); // 算法4
if ans1 != ans2 || ans1 != ans3 || ans1 != ans4 {
println!("出错了!");
}
}
println!("功能测试结束");
println!("性能测试开始");
let n = 300000usize;
let v = 1000000000;
let test_time = 10;
println!("数组长度 : {}", n);
println!("数值范围 : {}", v);
println!("测试次数 : {}", test_time);
let mut run_time = Duration::new(0, 0);
for _ in 0..test_time {
let arr = random_array(n, v);
let start = Instant::now();
min_op4(&arr);
let end = Instant::now();
run_time += end - start;
}
println!(
"{}次测试总运行时间 : {} 毫秒",
test_time,
run_time.as_millis()
);
println!("性能测试结束");
}
// 算法1:暴力枚举
fn min_op1(arr: &Vec<i32>) -> i32 {
let max = arr.iter().max().unwrap();
let mut op = vec![false; (*max + 1) as usize];
process1(&mut op, &arr, 0, *max)
}
// 算法1的辅助函数
fn process1(op: &mut Vec<bool>, arr: &Vec<i32>, num: i32, max: i32) -> i32 {
if num == max + 1 {
let mut cnt = 0;
let mut help = vec![0; arr.len()];
for i in 0..arr.len() {
help[i] = arr[i];
}
for i in 0..=max {
if op[i as usize] {
cnt += 1;
add(&mut help, i);
}
}
for i in 1..arr.len() {
if help[i - 1] > help[i] {
return std::i32::MAX;
}
}
return cnt;
} else {
op[num as usize] = true;
let p1 = process1(op, arr, num + 1, max);
op[num as usize] = false;
let p2 = process1(op, arr, num + 1, max);
return p1.min(p2);
}
}
// 算法1的辅助函数,将数组中等于num的元素都加一
fn add(arr: &mut Vec<i32>, num: i32) {
for i in 0..arr.len() {
if arr[i] == num {
arr[i] += 1;
}
}
}
// 算法2:利用动态规划
fn min_op2(arr: &[i32]) -> i32 {
if arr.len() < 2 {
return 0;
}
let n = arr.len() as i32;
let mut min = vec![0; n as usize];
min[(n - 1) as usize] = arr[(n - 1) as usize];
let mut i = n - 2;
while i >= 0 {
min[i as usize] = std::cmp::min(min[(i + 1) as usize], arr[i as usize]);
i -= 1;
}
let max = *arr.iter().max().unwrap();
let mut add = vec![false; max as usize + 1];
for i in 0..n - 1 {
if arr[i as usize] > min[(i + 1) as usize] {
for j in min[(i + 1) as usize]..arr[i as usize] {
add[j as usize] = true;
}
}
}
add.into_iter().filter(|&is| is).count() as i32
}
// 算法3:利用单调栈
fn min_op3(arr: &[i32]) -> i32 {
let n = arr.len();
let mut m = 0;
for num in arr.iter() {
m = m.max(*num);
}
let mut dst = DynamicSegmentTree::new(m);
let mut max = arr[0];
for i in 1..n {
if max > arr[i] {
dst.set(arr[i], max - 1);
}
max = max.max(arr[i]);
}
dst.sum()
}
struct Node {
sum: i32,
set: bool,
left: Option<Box<Node>>,
right: Option<Box<Node>>,
}
impl Node {
fn new() -> Self {
Node {
sum: 0,
set: false,
left: None,
right: None,
}
}
fn push_down(&mut self, ln: i32, rn: i32) {
if self.left.is_none() {
self.left = Some(Box::new(Node::new()));
}
if self.right.is_none() {
self.right = Some(Box::new(Node::new()));
}
if self.set {
self.left.as_mut().unwrap().set = true;
self.right.as_mut().unwrap().set = true;
self.left.as_mut().unwrap().sum = ln;
self.right.as_mut().unwrap().sum = rn;
self.set = false;
}
}
}
struct DynamicSegmentTree {
root: Node,
size: i32,
}
impl DynamicSegmentTree {
fn new(max: i32) -> Self {
let root = Node::new();
DynamicSegmentTree { root, size: max }
}
fn set(&mut self, s: i32, e: i32) {
Self::update(&mut self.root, 0, self.size, s, e);
}
fn update(c: &mut Node, l: i32, r: i32, s: i32, e: i32) {
if s <= l && r <= e {
c.set = true;
c.sum = r - l + 1;
} else {
let mid = (l + r) >> 1;
c.push_down(mid - l + 1, r - mid);
if s <= mid {
if c.left.is_none() {
c.left = Some(Box::new(Node::new()));
}
DynamicSegmentTree::update(c.left.as_mut().unwrap(), l, mid, s, e);
}
if e > mid {
if c.right.is_none() {
c.right = Some(Box::new(Node::new()));
}
DynamicSegmentTree::update(c.right.as_mut().unwrap(), mid + 1, r, s, e);
}
c.sum = c.left.as_ref().unwrap().sum + c.right.as_ref().unwrap().sum;
}
}
fn sum(&self) -> i32 {
self.root.sum
}
}
// 算法4:将数组转化为差分数组,统计所有负数的绝对值之和
fn min_op4(arr: &[i32]) -> i32 {
let n = arr.len();
let m = arr.iter().max().unwrap();
unsafe {
for i in 0..CNT {
LCHILD[i] = -1;
RCHILD[i] = -1;
}
CNT = 0;
SUM[CNT] = 0;
SET[CNT] = false;
LEFT[CNT] = 0;
RIGHT[CNT] = *m;
CNT += 1;
let mut max = arr[0];
for i in 1..n {
if max > arr[i] {
set(arr[i], max - 1, 0);
}
max = std::cmp::max(max, arr[i]);
}
sum()
}
}
const MAX_M: usize = 8000000;
static mut SUM: [i32; MAX_M] = [0; MAX_M];
static mut SET: [bool; MAX_M] = [false; MAX_M];
static mut LEFT: [i32; MAX_M] = [0; MAX_M];
static mut RIGHT: [i32; MAX_M] = [0; MAX_M];
static mut LCHILD: [i32; MAX_M] = [-1; MAX_M];
static mut RCHILD: [i32; MAX_M] = [-1; MAX_M];
// 全局初始化函数(需要在安全代码块中使用)
unsafe fn init() {
for i in 0..MAX_M {
LCHILD[i] = -1;
RCHILD[i] = -1;
}
}
static mut CNT: usize = 0;
unsafe fn set(s: i32, e: i32, i: usize) {
let l = LEFT[i];
let r = RIGHT[i];
if s <= l && r <= e {
SET[i] = true;
SUM[i] = r - l + 1;
} else {
let mid = (l + r) >> 1;
down(i, l, mid, mid + 1, r, mid - l + 1, r - mid);
if s <= mid {
set(s, e, LCHILD[i] as usize);
}
if e > mid {
set(s, e, RCHILD[i] as usize);
}
SUM[i] = SUM[LCHILD[i] as usize] + SUM[RCHILD[i] as usize];
}
}
unsafe fn down(i: usize, l1: i32, r1: i32, l2: i32, r2: i32, ln: i32, rn: i32) {
if LCHILD[i] == -1 {
SUM[CNT] = 0;
SET[CNT] = false;
LEFT[CNT] = l1;
RIGHT[CNT] = r1;
LCHILD[i] = CNT as i32;
CNT += 1;
}
if RCHILD[i] == -1 {
SUM[CNT] = 0;
SET[CNT] = false;
LEFT[CNT] = l2;
RIGHT[CNT] = r2;
RCHILD[i] = CNT as i32;
CNT += 1;
}
if SET[i] {
SET[LCHILD[i] as usize] = true;
SET[RCHILD[i] as usize] = true;
SUM[LCHILD[i] as usize] = ln;
SUM[RCHILD[i] as usize] = rn;
SET[i] = false;
}
}
unsafe fn sum() -> i32 {
SUM[0]
}
// 为了测试
// 辅助函数:生成随机数组
fn random_array(n: usize, v: i32) -> Vec<i32> {
let mut ans = vec![0; n];
for i in 0..n {
ans[i] = rand::random::<i32>() % v;
ans[i] = (ans[i] + v) % v;
}
ans
}
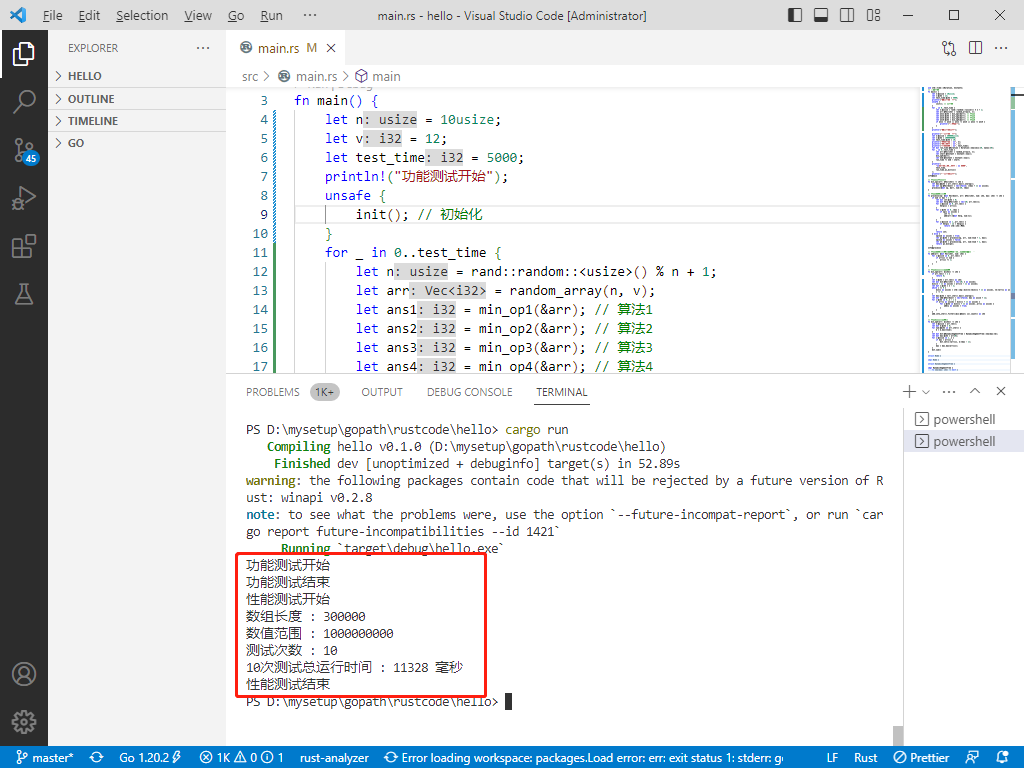
结果如下:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号