2023-04-14:n对情侣坐在连续排列的 2n 个座位上,想要牵到对方的手, 人和座位由一个整数数组 row 表示,其中 row[i] 是坐在第 i 个座位上的人的ID, 情侣们按顺序编号,第一对
2023-04-14:n对情侣坐在连续排列的 2n 个座位上,想要牵到对方的手,
人和座位由一个整数数组 row 表示,其中 row[i] 是坐在第 i 个座位上的人的ID,
情侣们按顺序编号,第一对是 (0, 1),第二对是 (2, 3),以此类推,最后一对是 (2n-2, 2n-1)。
返回 最少交换座位的次数,以便每对情侣可以并肩坐在一起。
每次交换可选择任意两人,让他们站起来交换座位。
输入: row = [0,2,1,3]。
输出: 1。
输入: row = [3,2,0,1]。
输出: 0。
答案2023-04-14:
大体过程如下:
-
定义并查集结构体 UnionFind,包括父节点数组 father、子树大小数组 size、辅助数组 help 和当前连通分量数 sets。
-
实现并查集结构体的三个方法:
a. 初始化方法 new,初始化父节点数组和子树大小数组,并将父节点数组的值初始化为自身,连通分量数初始为节点数量。
b. 查找方法 find,通过不断向上寻找父节点,直到找到根节点,并压缩路径优化查找效率。
c. 合并方法 union,找到 i 和 j 所在的连通分量的代表元素 fi 和 fj,以子树大小来优化合并操作,并更新连通分量数。
-
实现计算最少交换座位次数的函数 min_swaps_couples,首先获取座位数量 n,然后初始化并查集 uf,遍历相邻的座位,将情侣所在的连通分量合并。最后返回需要交换座位的最小次数。
-
在 main 函数中分别调用 min_swaps_couples 函数,传入测试数据,并输出最少交换座位的次数。
-
根据测试数据 row = [0, 2, 1, 3],第一对情侣坐在座位0和1上,第二对情侣坐在座位2和3上,因此已经满足牵手的条件。而在测试数据 row = [3, 2, 0, 1] 中,第一对情侣坐在座位3和2上,第二对情侣坐在座位0和1上,因此需要交换他们的座位才能满足牵手的条件。
并查集的初始化时间复杂度为O(n),其中n为节点数量。在计算最少交换座位次数的函数 min_swaps_couples 中,遍历相邻的座位需要O(n) 的时间,每次调用并查集中的 find 方法和 union 方法的时间复杂度均为O(α(n)),其中α(n) 是阿克曼函数的反函数,它比对数函数增长得慢,可以近似看作常数级别。因此,总时间复杂度为O(nα(n))。
空间复杂度取决于节点数量,需要使用O(n) 的空间存储父节点数组、子树大小数组和辅助数组。
rust代码如下:
// 定义并查集结构体
struct UnionFind {
father: Vec<i32>, // 父节点数组
size: Vec<i32>, // 子树大小数组
help: Vec<i32>, // 辅助数组,用于优化路径压缩操作
sets: i32, // 当前连通分量数
}
impl UnionFind {
// 初始化并查集
fn new(n: i32) -> Self {
let mut father = vec![0; n as usize]; // 初始化父节点数组
let size = vec![1; n as usize]; // 初始化子树大小数组
for i in 0..n {
father[i as usize] = i; // 父节点初始化为自身
}
UnionFind {
father, // 返回新建的并查集结构体
size,
help: vec![0; n as usize],
sets: n, // 初始时连通分量数为n
}
}
// 查找i所在连通分量的代表元素
fn find(&mut self, mut i: i32) -> i32 {
let mut hi = 0;
while i != self.father[i as usize] {
// 不断向上寻找父节点,直到找到根节点
self.help[hi] = i; // 将当前节点压入辅助数组中
hi += 1;
i = self.father[i as usize]; // 向上跳一步
}
for j in (0..hi).rev() {
// 压缩路径
self.father[self.help[j] as usize] = i; // 将辅助数组中的节点的父节点设为根节点
}
i // 返回根节点
}
// 合并i和j所在的连通分量
fn union(&mut self, i: i32, j: i32) {
let fi = self.find(i); // 找到i的代表元素
let fj = self.find(j); // 找到j的代表元素
if fi != fj {
// 如果i和j不在同一个连通分量中
if self.size[fi as usize] >= self.size[fj as usize] {
// 以树的大小来优化合并操作
self.father[fj as usize] = fi; // 将fj的父节点设为fi
self.size[fi as usize] += self.size[fj as usize]; // 更新fi子树的大小
} else {
self.father[fi as usize] = fj; // 将fi的父节点设为fj
self.size[fj as usize] += self.size[fi as usize]; // 更新fj子树的大小
}
self.sets -= 1; // 连通分量数减1
}
}
// 获取当前连通分量数
fn sets(&self) -> i32 {
self.sets
}
}
// 计算最少交换座位的次数
fn min_swaps_couples(row: Vec<i32>) -> i32 {
let n = row.len() as i32; // 座位数量
let mut uf = UnionFind::new(n / 2); // 初始化并查集
for i in (0..n).step_by(2) {
// 遍历相邻的座位
uf.union(row[i as usize] / 2, row[(i + 1) as usize] / 2); // 合并情侣所在的连通分量
}
n / 2 - uf.sets() // 返回需要交换座位的最小次数
}
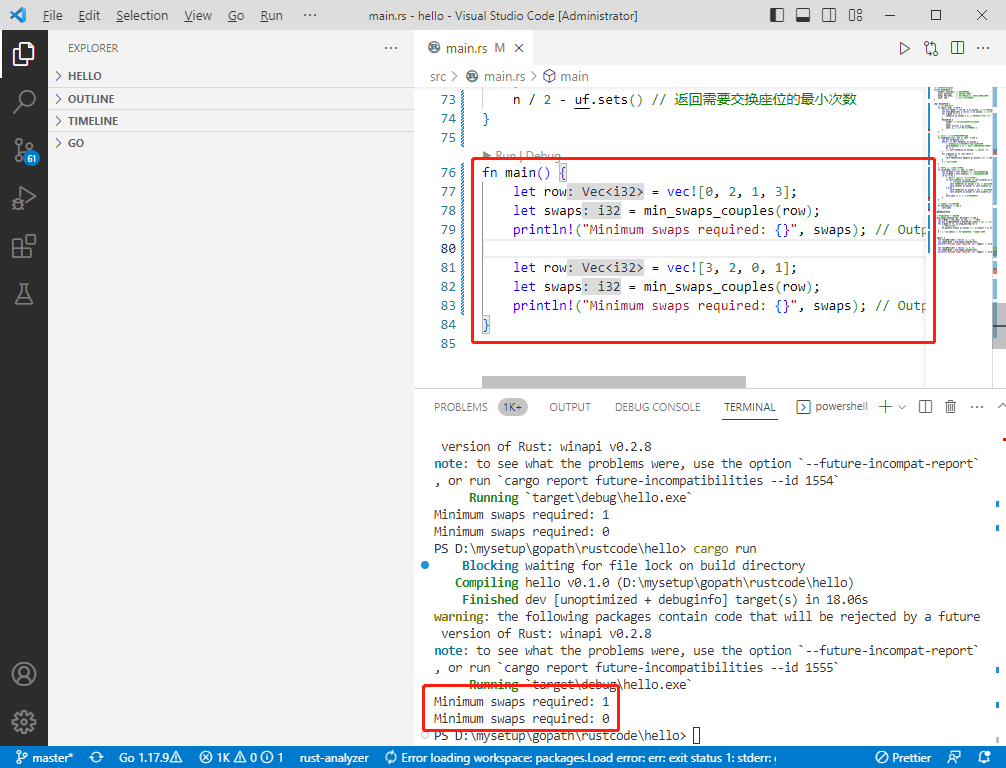
fn main() {
let row = vec![0, 2, 1, 3];
let swaps = min_swaps_couples(row);
println!("Minimum swaps required: {}", swaps); // Output: Minimum swaps required: 1
let row = vec![3, 2, 0, 1];
let swaps = min_swaps_couples(row);
println!("Minimum swaps required: {}", swaps); // Output: Minimum swaps required: 0
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号