2022-04-25:给定两个长度为N的数组,a[]和b[] 也就是对于每个位置i来说,有a[i]和b[i]两个属性 i a[i] b[i] j a[j] b[j] 现在想为了i,选一个最
2022-04-25:给定两个长度为N的数组,a[]和b[]
也就是对于每个位置i来说,有a[i]和b[i]两个属性
i a[i] b[i]
j a[j] b[j]
现在想为了i,选一个最好的j位置,搭配能得到最小的如下值:
(a[i] + a[j]) ^ 2 + b[i] + b[j]
我们把这个最小的值,定义为i的最in值
比如 :
a = { 2, 3, 6, 5, 1 }
b = { 100, 70, 20, 40, 150 }
0 1 2 3 4
0位置和2位置搭配,可以得到最in值 : 184
1位置和2位置搭配,可以得到最in值 : 171
2位置和1位置搭配,可以得到最in值 : 171
3位置和1位置搭配,可以得到最in值 : 174
4位置和2位置搭配,可以得到最in值 : 219
注意 : i位置可以和i位置(自己)搭配,并不是说i和j一定要是不同的位置
返回每个位置i的最in值
比如上面的例子,最后返回[184, 171, 171, 174, 219]
1 <= N <= 10^5
1 <= a[i]、b[i] <= 10^9
来自第四届全国大学生算法设计与编程挑战赛(秋季赛)。
答案2022-04-25:
题目描述:给定两个长度为 N 的数组 a[] 和 b[],对于每个位置 i,有 a[i] 和 b[i] 两个属性。现在想为了 i,选一个最优的 j 位置,搭配能得到最小的值 (a[i]+a[j])^2+b[i]+b[j]。定义这个最小的值为 i 的最 in 值。求返回每个位置 i 的最 in 值。
解法一:暴力法
-
遍历数组 a 和 b,依次计算出每个位置 i 和 j 的最 in 值。
-
对于每个位置 i,遍历数组 a 和 b,计算出所有的最小值。
-
返回所有位置的最小值。
时间复杂度:O(N^2)。
空间复杂度为 O(N),因为需要存储数组 ans。
解法二:正式方法
-
计算出每个位置 S(j)=2a[j] 和 T(j)=a[j]^2+b[j]。
-
将所有位置按照 S(j) 从大到小排序。
-
新建一个栈,对每个位置 i 进行遍历,找到最好的 j 位置,使得 S(j)+T(j)/a[i] 最小,并将其压入栈中。
-
将所有位置按照 a 值从大到小排序。
-
对每个位置 i 进行遍历,寻找最好的 j 位置,计算出最小的值,返回所有位置的最小值。
时间复杂度:O(N*logN)。
空间复杂度为 O(N),因为需要存储数组 st、stack 和 arr。其中,st 数组用于存储 S(j) 和 T(j) 的值,stack 数组用于实现单调栈,arr 数组用于排序和计算答案。
注意事项:
-
在第三步中,需要使用单调栈来寻找最好的 j 位置。
-
在第五步中,可以通过数学公式推导得到最小值,而不需要逐一计算每个位置的最小值。
go完整代码如下:
package main
import (
"fmt"
"math"
"math/rand"
"sort"
"time"
)
// 暴力方法
// 时间复杂度O(N^2)
// 为了测试
func inValues1(a []int, b []int) []int64 {
n := len(a)
ans := make([]int64, n)
for i := 0; i < n; i++ {
curAns := int64(math.MaxInt64)
for j := 0; j < n; j++ {
cur := int64((a[i]+a[j])*(a[i]+a[j]) + b[i] + b[j])
curAns = min(curAns, cur)
}
ans[i] = curAns
}
return ans
}
func min(x, y int64) int64 {
if x < y {
return x
}
return y
}
// 正式方法
// 时间复杂度O(N*logN)
// (a[i] + a[j]) ^ 2 + b[i] + b[j]
// a[i]^2 + b[i] + 2a[i]a[j] + a[j]^2 + b[j]
// a[i] * ( a[i] + b[i]/a[i] + 2a[j] + (a[j]^2 + b[j])/a[i])
// 令S(j) = 2a[j]
// 令T(j) = a[j]^2 + b[j]
// 那么对于i来说,就是选择j,让下面得到最小值
// a[i] * ( a[i] + b[i]/a[i] + S(j) + T(j)/a[i])
// 选择最小的S(j) + T(j)/a[i],就得到了答案
// 剩下的一切都是围绕这个
func inValues2(a []int, b []int) []int64 {
n := len(a)
// i a[i] b[i]
// i s[i] t[i]
st := make([][2]int64, n)
for i := 0; i < n; i++ {
st[i][0] = 2 * int64(a[i])
st[i][1] = int64(a[i]*a[i]) + int64(b[i])
}
// 只需要根据S值从大到小排序即可
// 下面的比较器定义稍复杂,因为go里没有泛型sort,只能自己写
// 所以策略参考了S和T,其实只需要根据S值从大到小排序即可
sort.Slice(st, func(i, j int) bool {
if st[i][0] != st[j][0] {
return st[i][0] > st[j][0]
}
return st[i][1] <= st[j][1]
})
stack := make([]int, n)
r := 0
for i := 0; i < n; i++ {
// s 大 -> 小
s := st[i][0]
t := st[i][1]
for r > 0 && tail(st, stack, r) >=
better(st[stack[r-1]][0], st[stack[r-1]][1], s, t) {
r--
}
stack[r] = i
r++
}
arr := make([][3]int, n)
for i := 0; i < n; i++ {
arr[i][0] = i
arr[i][1] = a[i]
arr[i][2] = b[i]
}
// 只需要根据a值从大到小排序即可
sort.Slice(arr, func(i, j int) bool {
if arr[i][1] != arr[j][1] {
return arr[i][1] > arr[j][1]
}
return arr[i][0] < arr[j][0]
})
ans := make([]int64, n)
for k := 0; k < n; k++ {
i := arr[k][0]
ai := arr[k][1]
bi := arr[k][2]
for tail(st, stack, r) > int64(ai) {
r--
}
sj := st[stack[r-1]][0]
tj := st[stack[r-1]][1]
// a[i] * ( a[i] + b[i]/a[i] + S(j) + T(j)/a[i])
curAns := sj*int64(ai) + tj + int64(ai)*int64(ai) + int64(bi)
ans[i] = curAns
}
return ans
}
func tail(st [][2]int64, deque []int, r int) int64 {
if r == 1 {
return 1
}
return better(st[deque[r-2]][0], st[deque[r-2]][1], st[deque[r-1]][0], st[deque[r-1]][1])
}
// 入参时候s1>=s2,这是一定的
// 返回当ai大到什么值的时候,(s2+t2/ai) <= (s1+t1/ai)
// 即 : ai大
func better(s1, t1, s2, t2 int64) int64 {
if s1 == s2 {
if t1 <= t2 {
return math.MaxInt64
}
return 1
}
// s1 > s2
if t1 >= t2 {
return 1
}
// s1 > s2
// t1 < t2
td := t2 - t1
sd := s1 - s2
return (td + sd - 1) / sd
}
// 为了测试
func randomArray(n, v int) []int {
ans := make([]int, n)
for i := 0; i < n; i++ {
ans[i] = rand.Intn(v) + 1
}
return ans
}
// 为了测试
func isSameArray(arr1, arr2 []int64) bool {
for i := 0; i < len(arr1); i++ {
if arr1[i] != arr2[i] {
return false
}
}
return true
}
// 为了测试
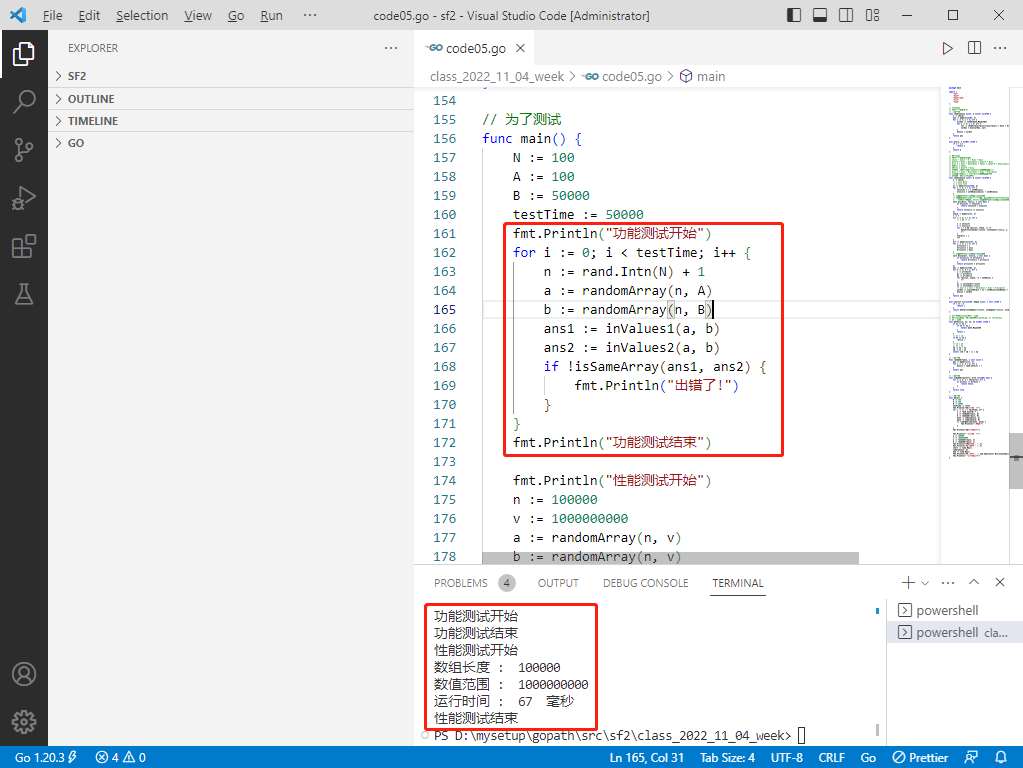
func main() {
N := 100
A := 100
B := 50000
testTime := 50000
fmt.Println("功能测试开始")
for i := 0; i < testTime; i++ {
n := rand.Intn(N) + 1
a := randomArray(n, A)
b := randomArray(n, B)
ans1 := inValues1(a, b)
ans2 := inValues2(a, b)
if !isSameArray(ans1, ans2) {
fmt.Println("出错了!")
}
}
fmt.Println("功能测试结束")
fmt.Println("性能测试开始")
n := 100000
v := 1000000000
a := randomArray(n, v)
b := randomArray(n, v)
fmt.Println("数组长度 : ", n)
fmt.Println("数值范围 : ", v)
start := time.Now()
inValues2(a, b)
end := time.Now()
fmt.Println("运行时间 : ", end.Sub(start).Milliseconds(), " 毫秒")
fmt.Println("性能测试结束")
}
rust完整代码如下:
use std::time::Instant;
// 暴力方法
// 时间复杂度O(N^2)
// 为了测试
fn in_values1(a: &Vec<i32>, b: &Vec<i32>) -> Vec<i64> {
let n = a.len();
let mut ans = vec![0; n];
for i in 0..n {
let mut cur_ans = i64::MAX;
for j in 0..n {
let cur = (a[i] + a[j]).pow(2) as i64 + b[i] as i64 + b[j] as i64;
cur_ans = cur_ans.min(cur);
}
ans[i] = cur_ans;
}
ans
}
// 正式方法
// 时间复杂度O(N*logN)
// (a[i] + a[j]) ^ 2 + b[i] + b[j]
// a[i]^2 + b[i] + 2a[i]a[j] + a[j]^2 + b[j]
// a[i] * ( a[i] + b[i]/a[i] + 2a[j] + (a[j]^2 + b[j])/a[i])
// 令S(j) = 2a[j]
// 令T(j) = a[j]^2 + b[j]
// 那么对于i来说,就是选择j,让下面得到最小值
// a[i] * ( a[i] + b[i]/a[i] + S(j) + T(j)/a[i])
// 选择最小的S(j) + T(j)/a[i],就得到了答案
// 剩下的一切都是围绕这个
fn in_values2(a: &Vec<i32>, b: &Vec<i32>) -> Vec<i64> {
let n = a.len();
let mut st = vec![vec![0; 2]; n];
for i in 0..n {
st[i][0] = (a[i] * 2) as i64;
st[i][1] = (a[i] * a[i] + b[i]) as i64;
}
st.sort_by(|x, y| {
if x[0] != y[0] {
y[0].cmp(&x[0])
} else {
x[1].cmp(&y[1])
}
});
let mut stack = vec![0; n];
let mut r = 0;
for i in 0..n {
let s = st[i][0];
let t = st[i][1];
while r > 0
&& tail(&st, &stack, r)
>= better(
st[stack[(r - 1) as usize] as usize][0],
st[stack[(r - 1) as usize] as usize][1],
s,
t,
)
{
r -= 1;
}
stack[r as usize] = i as i32;
r += 1;
}
let mut arr = vec![(0, 0, 0); n];
for i in 0..n {
arr[i] = (i, a[i], b[i]);
}
arr.sort_by(|x, y| {
if x.1 != y.1 {
y.1.cmp(&x.1)
} else {
x.0.cmp(&y.0)
}
});
let mut ans = vec![0; n];
for k in 0..n {
let i = arr[k].0;
let ai = arr[k].1;
let bi = arr[k].2;
while tail(&st, &stack, r as i32) > ai {
r -= 1;
}
let sj = st[stack[(r - 1) as usize] as usize][0];
let tj = st[stack[(r - 1) as usize] as usize][1];
let cur_ans = sj * ai as i64 + tj + ai as i64 * ai as i64 + bi as i64;
ans[i] = cur_ans;
}
ans
}
// 返回当ai大到什么值的时候,后者更好
fn tail(st: &Vec<Vec<i64>>, deque: &Vec<i32>, r: i32) -> i32 {
if r == 1 {
return 1;
}
let (s1, t1) = (
st[deque[r as usize - 2] as usize][0],
st[deque[r as usize - 2] as usize][1],
);
let (s2, t2) = (
st[deque[r as usize - 1] as usize][0],
st[deque[r as usize - 1] as usize][1],
);
better(s1, t1, s2, t2)
}
// 入参时候s1>=s2,这是一定的
// 返回当ai大到什么值的时候,(s2+t2/ai) <= (s1+t1/ai)
// 即 : ai大到什么值的时候,后者更好
fn better(s1: i64, t1: i64, s2: i64, t2: i64) -> i32 {
if s1 == s2 {
if t1 <= t2 {
std::i32::MAX
} else {
1
}
} else if t1 >= t2 {
1
} else {
// s1 > s2
let td = t2 - t1;
let sd = s1 - s2;
((td + sd - 1) / sd) as i32
}
}
fn random_array(n: usize, v: i32) -> Vec<i32> {
let mut ans = vec![0; n];
for i in 0..n {
ans[i] = (rand::random::<usize>() % (v as usize) + 1) as i32;
}
ans
}
fn is_same_array(arr1: &Vec<i64>, arr2: &Vec<i64>) -> bool {
if arr1.len() != arr2.len() {
return false;
}
for i in 0..arr1.len() {
if arr1[i] != arr2[i] {
return false;
}
}
true
}
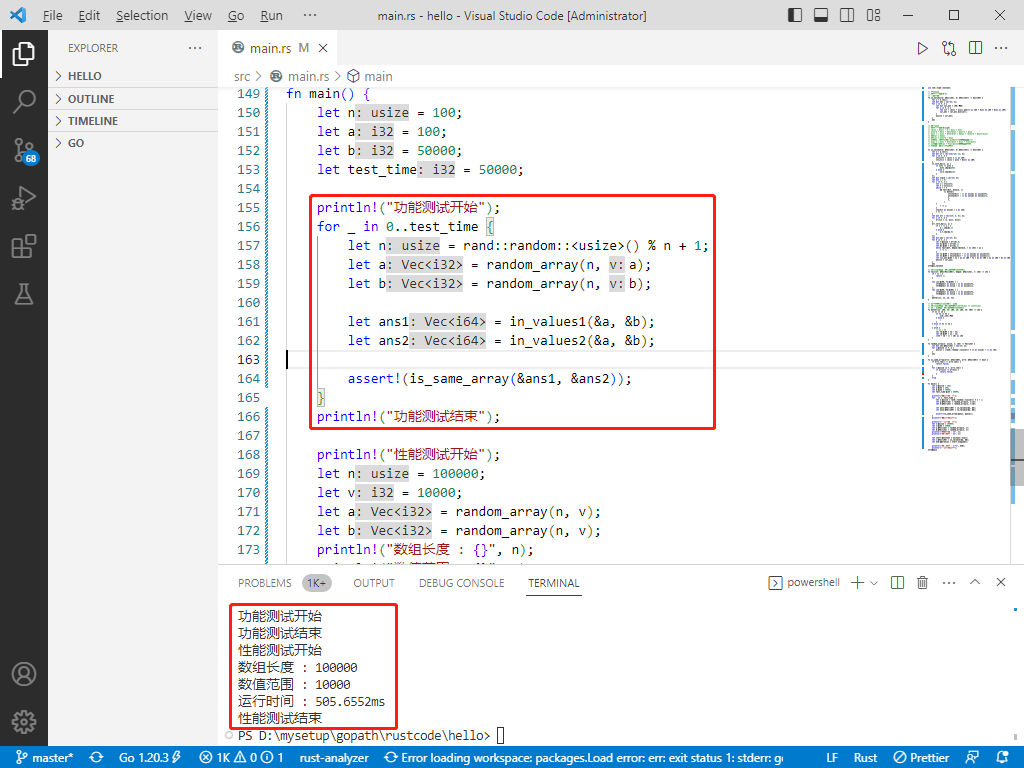
fn main() {
let n = 100;
let a = 100;
let b = 50000;
let test_time = 50000;
println!("功能测试开始");
for _ in 0..test_time {
let n = rand::random::<usize>() % n + 1;
let a = random_array(n, a);
let b = random_array(n, b);
let ans1 = in_values1(&a, &b);
let ans2 = in_values2(&a, &b);
assert!(is_same_array(&ans1, &ans2));
}
println!("功能测试结束");
println!("性能测试开始");
let n = 100000;
let v = 10000;
let a = random_array(n, v);
let b = random_array(n, v);
println!("数组长度 : {}", n);
println!("数值范围 : {}", v);
let start = Instant::now();
let c = in_values2(&a, &b);
let end = start.elapsed();
println!("运行时间 : {:?}", end);
println!("性能测试结束");
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号