同余公式和性质[转]

基本性质：

（1）若p|(a-b)，则a≡b (% p)。例如 11 ≡ 4 (% 7)， 18 ≡ 4(% 7)

（2）(a % p)=(b % p)意味a≡b (% p)

（3）对称性：a≡b (% p)等价于b≡a (% p)

（4）传递性：若a≡b (% p)且b≡c (% p) ，则a≡c (% p)

运算规则：

模运算与基本四则运算有些相似，但是除法例外。其规则如下：
(a + b) % p = (a % p + b % p) % p （1）
(a - b) % p = (a % p - b % p) % p （2）
(a * b) % p = (a % p * b % p) % p （3）
ab % p = ((a % p)b) % p （4）

结合率： ((a+b) % p + c) % p = (a + (b+c) % p) % p （5）

((a*b) % p * c)% p = (a * (b*c) % p) % p （6）

交换率： (a + b) % p = (b+a) % p （7）

(a * b) % p = (b * a) % p （8）

分配率： ((a +b)% p * c) % p = ((a * c) % p + (b * c) % p) % p （9）

重要定理：若a≡b (% p)，则对于任意的c，都有(a + c) ≡ (b + c) (%p)；（10）

若a≡b (% p)，则对于任意的c，都有(a * c) ≡ (b * c) (%p)；（11）

若a≡b (% p)，c≡d (% p)，则 (a + c) ≡ (b + d) (%p)，(a - c) ≡ (b - d) (%p)，

(a * c) ≡ (b * d) (%p)，(a / c) ≡ (b / d) (%p)； （12）

若a≡b (% p)，则对于任意的c，都有ac≡ bc (%p)； （13）

第二组性质：

1.如果 a /equiv b /pmod{m}，那么 m | (a − b) ，这里 m | (a − b) 表示 (a − b) 能被 m 整除

2.如果 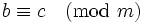a /equiv b /pmod{m}，b /equiv c /pmod{m}, 那么a /equiv c /pmod{m}

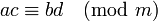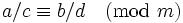
3.如果 a /equiv b /pmod{m}，c /equiv d/pmod{m}, 那么a+c /equiv b+d /pmod{m}，a-c /equiv b-d /pmod{m}，ac /equiv bd /pmod{m}，a/c /equiv b /d /pmod{m}

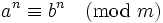
4如果 a /equiv b /pmod{m}， 那么 a^n /equiv b^n /pmod{m}

5. 如果ac≡bc(mod m)，且c和m互质，则a≡b(mod m）

posted @ 2011-10-24 19:19  moonbay  阅读(302)  评论(0)  编辑  收藏  举报