序列

题源

资产阶级学术权威的题解

---

 题面

 

---

 使用DP

我们记录 dp[i][j]为 长为i，最大值不超过j的答案

pre[ i ][ j ] = sum( pre[ i ][ k ], k=[ 0 , j ] )

---

  

首先我们会发现它们是一组长度连续增加一，且相邻两个序列只有一个数不一样（如下图）

  

---

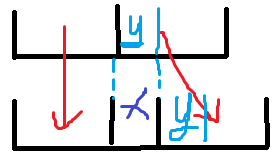
由于保证字典序上升，所以 x 应该不小于它上面的 y

也就是一个新数不小于它后面的数

---

 我们可以想成一个序列

每次操作让一个数在它前面“长出”一个比它大的数

新数的下界取决于旧数

所以 x 以前（a） 和 y 以后（b） 是相互独立的

a 全部比y 大

我们把a 看做由一个地基为y的地面上长出来的一个最大值不超过(y+mx)的序列

由[0,现在单个元素的最大值-1]枚举mx，发现是一个前缀和

 

---

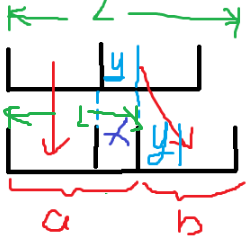
 所以我们要让y 前长出一个长为l的x 

所获得的价值是对于 每个x 可行的a*b的值

当然，x中的元素 所在的位置不知道

所以还要乘上 x中元素可能取得的位置 C(L-2,l-1) 

---

Code : 406ms/79248kb

#include<stdio.h>
#define int long long
#define For(i,a,b) for(register long long i=(a);i<=(b);i++)
using namespace std;
const int maxn=310;
int n,k,mod,c[maxn][maxn],pre[maxn][maxn],dp[maxn][maxn];
void init(){
    For(i,0,maxn-10) c[i][0]=c[i][i]=1;
    For(i,1,maxn-10){
        For(j,1,i-1){
            c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
        }
    }
    For(i,0,k){
        dp[0][i]=dp[1][i]=1;
        pre[0][i]=pre[1][i]=(i+1)%mod;
    }
}
signed main(){
    scanf("%lld%lld%lld",&n,&k,&mod);
    init();
    For(i,2,n+1){
        For(j,1,k){
            For(l,0,i-1){
                dp[i][j]=(dp[i][j]+dp[i-l][j]*c[i-2][l-1]%mod*pre[l][j-1])%mod;
            }
            pre[i][j]=(pre[i][j-1]+dp[i][j])%mod;
        }
    }
    printf("%lld\n",dp[n+1][k]);
}