網絡流Dinic

题源

假设我们已经知道了EK的写法，考虑 玄学 优化。

主要慢在一个地方，如果一次尝试寻找增广路没有鸟用，

 

那就真的没有鸟用了。

 

显然我们可以钦定它一直增广直到不能继续为止。

何时无法继续？不连通就停。

BFS判断是否联通：

 1 bool bfs(){
 2     memset(dis,-1,sizeof(dis));
 3     while(!Q.empty()){
 4         Q.pop();
 5     }
 6     dis[S]=0;
 7     Q.push(S);
 8     while(!Q.empty()){
 9         int u=Q.front();
10         Q.pop() ;
11         for(int i=head[u];i!=-1;i=edge[i].nxt){
12             int v=edge[i].v;
13             if(dis[v]==-1&&edge[i].w){
14                 dis[v]=dis[u]+1;
15                 Q.push(v); 
16             }
17         }
18     }
19     return dis[T]!=-1;
20 }

 

我们使用分层图，开个队列一直压入遍历。

 1 inline int dfs(int u,int exp){
 2     if(u==T)return exp;
 3     int flow=0,tmp=0;
 4     for(int i=head[u];i!=-1;i=edge[i].nxt){
 5         int v=edge[i].v;
 6         if(dis[v]==dis[u]+1&&edge[i].w>0){
 7             tmp=dfs(v,min(exp,edge[i].w));
 8             if(!tmp)continue;
 9             exp-=tmp; 
10             flow+=tmp;
11             edge[i].w-=tmp;
12             edge[i^1].w+=tmp;
13             if(!exp)break;
14         }
15     }
16     return flow;
17 }

 SAMPLE INPUT

4 2 30
4 3 20
2 3 20
2 1 30
1 3 40

SAMPLE OUTPUT

14

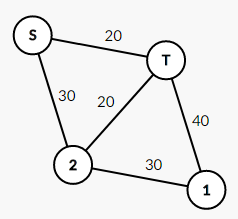
大样例：

SAMPLE INPUT

3 4 4
4 3 45
3 5 80
1 6 94
3 7 63
9 8 92
1 9 75
6 3 12
7 9 63
6 1 39
6 1 97
9 7 33
7 4 55
8 9 36
5 2 61
9 8 97
2 4 36
1 2 2
10 2 14
5 9 82
5 1 32
6 2 94
9 2 10
6 10 50
7 6 53

SAMPLE OUTPUT

36

  

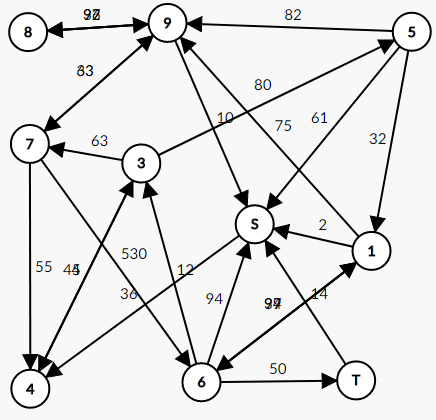
End.

posted @ 2019-07-19 21:35  monyhzc  阅读(111)  评论(0)  编辑  收藏  举报