机器学习系列1：线性回归

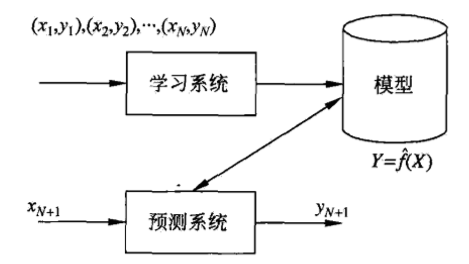
写在前面：机器学习主要分为监督学习、无监督学习和强化学习。本节内容主要针对监督学习下的线性回归进行简要说明及实现。机器学习开篇模型就是线性回归，简言之就是用一条直线较为准确的描述数据之间的关系，当出现新的数据的时候的时候，给出一个简单的预测值。

 

一、回归问题

　　回归问题是监督学习的一个重要问题，回归用于预测输入变量（自变量）和输出变量（因变量）之间的关系，特别的当输入变量的值发生变化时，输出变量的值随之发生改变。回归模型正是表示输入变量到输出变量之间映射的函数。

　　回归按照输入变量的个数，分为一元回归和多元回归；

　　回归按照输入变量和输出变量的关系类型，分为线性回归和非线性回归。　

　　

　　回归问题分为学习和预测两个过程，首先给定一个训练数据集：

　　　　T={(x₁,y₁),(x₂,y₂),...,(x_N,y_N)}

　　这里xi€Rⁿ是输入，y€R是对应的输出，i=1,2,...,N.

二、线性回归

• 假定：模型假定服从线性关系，即 y = ax+b or y = a₁x₁+a₂x₂+...+a_Nx_N

　　输出为离散的就是分类，输出为连续值就是回归，而我们初中学过的直线方程就是线性的。所以线性回归就是用线性的线来拟合一些回归的值。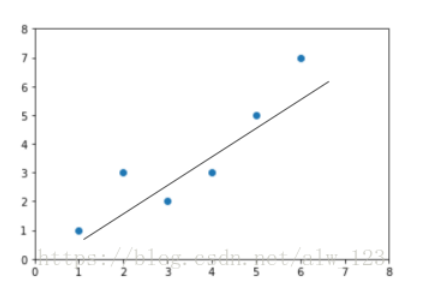

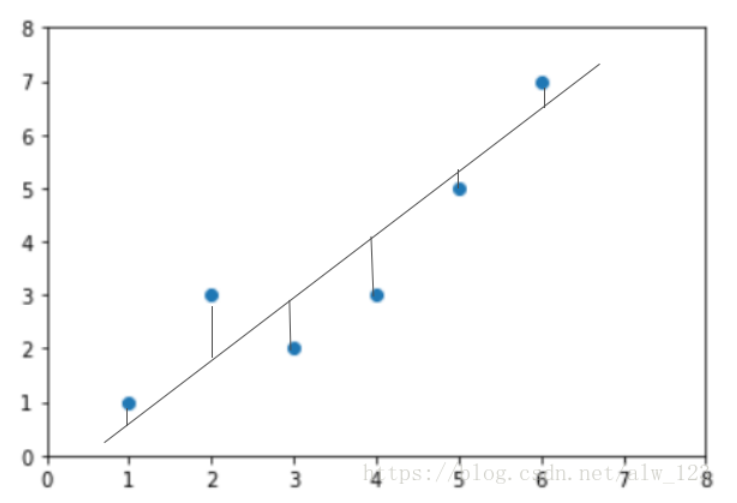
• 损失函数：常用的是平方损失

　　平方损失即欧氏距离，用来衡量预测值和真实值之间的距离误差的函数，这就是我们模型的一个评价标准，值越小说明我们越能拟合数据，反之值越大就说明模型的拟合能力越差。 

　　∑_i=1(y⁽ⁱ⁾-y_hat⁽ⁱ⁾)²

• 求解：最小二乘法

三、实战

• 数据准备

　　　y = 1.568*X + 0.283 + ε,ε服从高斯分布

　　用上面的式子产生真实数据样例，ε添加给模型的噪声，噪声满足均值为0，方差为0.1的高斯分布，随机采样100次，作为模型的训练数据。

　　

data = []
#构造样本数据
for i in range(100):
    x = np.random.uniform(-10.,10)
    eps = np.random.normal(0.,.1)#高斯噪声
    y = 1.568*x + 0.283 + eps
    data.append([x,y])
data = np.array(data)

 

• 误差计算

　　计算每个点(x⁽ⁱ⁾,y⁽ⁱ⁾)处的预测值和真实值之间差的平方并累加，得到训练集上的均方误差损失值。

def mse(b,w,points):
    err = 0#训练集总的误差累积
    for i in range(0,len(points)):
        x = points[i,0]
        y = points[i,1]
        err += (y - (w*x + b))**2
    return err / float(len(points))#得到平均误差

• 梯度计算

　　计算每个点的梯度信息，这里是简单地求导。

　　∂ℒ/∂𝑤 = (∂*(1/𝑛)Σ(𝑤𝑥⁽ⁱ⁾ + 𝑏 − 𝑦⁽ⁱ⁾)^2)  / ∂𝑤 

　　　　  = 2/𝑛 (Σ(𝑤𝑥⁽ⁱ⁾ + 𝑏 − 𝑦⁽ⁱ⁾) ∙ 𝑥(𝑖))

　  ∂ℒ/∂b = 2/𝑛 Σ(𝑤𝑥⁽ⁱ⁾ + 𝑏 − 𝑦⁽ⁱ⁾)

　　对计算出的w和b的梯度，按照公式进行更新：

　　𝒙′ = 𝒙 − 𝜂 ∙ ∇𝑓  ——>（x即 w，b）

def step_gradient(b_current, w_current, points, lr):
    # 计算误差函数在所有点上的导数,并更新w,b
    b_gradient = 0
    w_gradient = 0
    M = float(len(points)) # 总样本数
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
       # 误差函数对b 的导数,参考公式
        b_gradient += (2/M) * ((w_current * x + b_current) - y)
    　　# 误差函数对w 的导数,参考公式
        w_gradient += (2/M) * x * ((w_current * x + b_current) - y)
    # 根据梯度下降算法更新 w',b',其中lr 为学习率
    new_b = b_current - (lr * b_gradient)
    new_w = w_current - (lr * w_gradient)
    return [new_b, new_w]
    

• 梯度更新

　　根据上面计算新的w和b进行模型的迭代，所有样本训练一次我们成为一个Epoch。

　　

def gradient_descent(points, starting_b, starting_w, lr, num_iterations):
    # 循环更新w,b 多次
    b = starting_b # b 的初始值
    w = starting_w # w 的初始值
    # 根据梯度下降算法更新多次
    for step in range(num_iterations):
        # 计算梯度并更新一次
        b, w = step_gradient(b, w, np.array(points), lr)
        loss = mse(b, w, points) # 计算当前的均方差，用于监控训练进度
        if step%50 == 0: # 打印误差和实时的w,b 值
            print(f"iteration:{step}, loss:{loss}, w:{w}, b:{b}")
    return [b, w] # 返回最后一次的w,b        

• 主函数

def main():
    lr = 0.01 # 学习率
    initial_b = 0 # 初始化b 为0
    initial_w = 0 # 初始化w 为0
    num_iterations = 1000
    # 训练优化1000 次，返回最优w*,b*和训练Loss 的下降过程
    [b, w], losses = gradient_descent(data, initial_b, initial_w, lr, num_iterations)
    loss = mse(b, w, data) # 计算最优数值解w,b 上的均方差
    print(f'Final loss:{loss}, w:{w}, b:{b}')

• 最终结果

Final loss:0.012423128260963853,w:1.5674040004059528,b:0.2857226925947983

　　可以看到和我们最初构造数据的y = 1.568*X + 0.283 + ε很接近。也就是我们模型的拟合能力是很好的。

 

 补充说明：代码参考龙龙老师

四、总结

　　线性回归就是给定特征x情况下，通过f(模型)【映射】出y_hat(预测)。

　　X——>F(x)——>Y_hat

　　线性回归属于判别式模型、距离模型。