二进制减法的实现及负数在计算机中以补码存储原因
1.补码
对月亮来说，阴历每月十五是月圆之夜，即圆满。其他时间，只有一部分，而另一部分就是月亮的补码。对十进制来说，十就是圆满。对二进制来说，二就是圆满。用圆满减去某个数，就是某个数在此进制下的补码。但不论是十进制还是二进制，某一位的最大数总是比圆满之数小一。例如十进制的最大数是9，二进制的最大数是1，因此某个数的补码就是就是所有位数都变为最大的数减去这个数之后加一，例如十进制中22的补码就是99-22+1=78。二进制101101的补码就是111111-101101+1，刚好可以转化为所有位数取反+1，010010+1=10011。
2.补码和减法的关系
2.1.十进制
十以内的加减法用一位十进制就可以表示了，对于10-8来说，10+（8的补码）=10+2=12，因为只有一位来保存，只需要把进位舍弃就可以了。因此减法就转化为了补码的加法操作。
2.2.二进制
同十进制一样，10的二进制为（1010），8的二进制为（1000），8的二进制补码（1000），1010-1000来说，就是1010+（1000的补码）=10010，进的一位舍弃，结果为0010，符合结果。
3.负数在计算机中的表示
负数在计算机中是以对应正数补码的形式存储的，这样可以实现负数的加减和正数的加减统一
编程语言中，通常用32位二进制来存储整型（范围-231到231-1），最高位为符号位，0表示正数，1表示负数。如果只是简单的用符号位来表示负数，那么-3结果为10000000000000000000000000000011，4的结果是0000000000000000000000000000100，相加的结果为1000,0000,0000,0000,0000,0000,0000,0111（-7），明显不对。-3以3的补码形式表示为11111111111111111111111111111101，相加的结果为
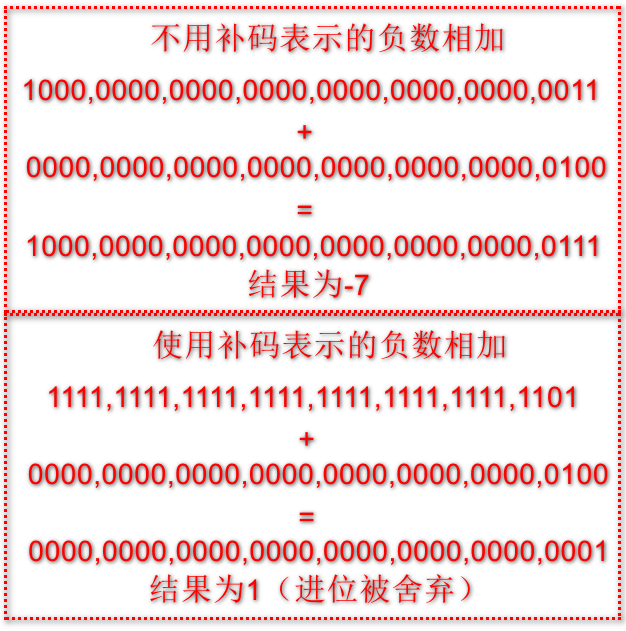
4.总结
补码可以将正整数的减法转化为减数和被减数的补码的加法
计算机中用正数的补码来存储负数，可以实现负数和负数，负数和正数的加减法的统一。
例如 5-（-2）=5+（-2的补码）= 5+（2的补码的补码）
