[NOIP2017 普及组] 棋盘
a要疯啦
[NOIP2017 普及组] 棋盘
点击查看复杂的题目
[NOIP2017 普及组] 棋盘
题目背景
NOIP2017 普及组 T3
题目描述
有一个的棋盘,棋盘上每一个格子可能是红色、黄色或没有任何颜色的。你现在要从棋盘的最左上角走到棋盘的最右下角。
任何一个时刻,你所站在的位置必须是有颜色的(不能是无色的), 你只能向上、 下、左、 右四个方向前进。当你从一个格子走向另一个格子时,如果两个格子的颜色相同,那你不需要花费金币;如果不同,则你需要花费 个金币。
另外, 你可以花费 个金币施展魔法让下一个无色格子暂时变为你指定的颜色。但这个魔法不能连续使用, 而且这个魔法的持续时间很短,也就是说,如果你使用了这个魔法,走到了这个暂时有颜色的格子上,你就不能继续使用魔法; 只有当你离开这个位置,走到一个本来就有颜色的格子上的时候,你才能继续使用这个魔法,而当你离开了这个位置(施展魔法使得变为有颜色的格子)时,这个格子恢复为无色。
现在你要从棋盘的最左上角,走到棋盘的最右下角,求花费的最少金币是多少?
输入格式
第一行包含两个正整数,以一个空格分开,分别代表棋盘的大小,棋盘上有颜色的格子的数量。
接下来的$ n x, y, c(x,y) c$。
其中 代表黄色, 代表红色。 相邻两个数之间用一个空格隔开。 棋盘左上角的坐标为,右下角的坐标为。
棋盘上其余的格子都是无色。保证棋盘的左上角,也就是 一定是有颜色的。
输出格式
一个整数,表示花费的金币的最小值,如果无法到达,输出。
样例 #1
样例输入 #1
5 7 1 1 0 1 2 0 2 2 1 3 3 1 3 4 0 4 4 1 5 5 0
样例输出 #1
8
样例 #2
样例输入 #2
5 5 1 1 0 1 2 0 2 2 1 3 3 1 5 5 0
样例输出 #2
-1
提示
输入输出样例 1 说明
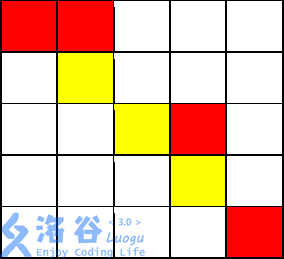
从开始,走到不花费金币
从向下走到花费 枚金币
从施展魔法,将变为黄色,花费 枚金币
从走到不花费金币
从走到不花费金币
从走到花费 枚金币
从走到花费 枚金币
从施展魔法,将变为黄色,花费 枚金币,
从走到不花费金币
从走到花费 枚金币
共花费 枚金币。
输入输出样例 2 说明
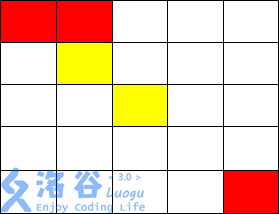
从走到,不花费金币
从走到,花费金币
施展魔法将变为黄色,并从走到花费 金币
从走到不花费金币
从只能施展魔法到达
而从以上四点均无法到达,故无法到达终点,输出
数据规模与约定
对于 的数据, 。
对于 的数据, 。
对于 的数据, 。
#include<bits/stdc++.h> using namespace std; int a[1005][1005],f[1005][1005],m,n,x,y,c; void dfs(int i,int j,int c,bool fl,int w) { if(i>m||i<1||j<1||j>m) { return; } f[i][j]=w; if(w+abs(c-a[i-1][j])<f[i-1][j]&&a[i-1][j]!=-1) { dfs(i-1,j,a[i-1][j],1,w+abs(c-a[i-1][j])); } if(w+abs(c-a[i][j-1])<f[i][j-1]&&a[i][j-1]!=-1) { dfs(i,j-1,a[i][j-1],1,w+abs(c-a[i][j-1])); } if(w+abs(c-a[i+1][j])<f[i+1][j]&&a[i+1][j]!=-1) { dfs(i+1,j,a[i+1][j],1,w+abs(c-a[i+1][j])); } if(w+abs(c-a[i][j+1])<f[i][j+1]&&a[i][j+1]!=-1) { dfs(i,j+1,a[i][j+1],1,w+abs(c-a[i][j+1])); } if(fl==1) { if(w+2<f[i-1][j]&&a[i-1][j]==-1) { dfs(i-1,j,c,0,w+2); } if(w+2<f[i][j-1]&&a[i][j-1]==-1) { dfs(i,j-1,c,0,w+2); } if(w+2<f[i+1][j]&&a[i+1][j]==-1) { dfs(i+1,j,c,0,w+2); } if(w+2<f[i][j+1]&&a[i][j+1]==-1) { dfs(i,j+1,c,0,w+2); } } return; } int main() { memset(a,-1,sizeof(a)); cin>>m>>n; for(int i=1; i<=n; i++) { cin>>x>>y>>c; a[x][y]=c; } memset(f,127,sizeof(f)); int s=f[m][m]; dfs(1,1,a[1][1],1,0); if(f[m][m]==s) { f[m][m]=-1; } cout<<f[m][m]<<endl; return 0; }
本文来自小默的博客,转载请注明原文链接:https://www.cnblogs.com/momotrace/p/woc-p3956.html








【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步