[NOIP1999 普及组] 导弹拦截

1.C++ 地球人口承载力2023-02-11 2.冒泡排序2023-02-11 3.棋盘移动2023-03-04 4.数的计数 c++2023-02-18 5.汉诺塔2023-02-16 6.「CSP-J2020」直播获奖 —— 桶排序例题2023-02-14 7.P1451 求细胞数量2023-03-18 8.迷宫问题2023-03-14 9.披萨大师2023-03-07 10.[NOIP2017 普及组] 棋盘2023-03-07 11.素数环2023-03-07 12.求排列(全排列问题)2023-03-07 13.数的组合2023-03-04 14.如何理解递归2023-03-04 15.关系网络2023-04-25 16.最短路径问题2023-04-23 17.红与黑2023-04-20 18.P1271 【深基9.例1】选举学生会2023-04-18 19.最短时间——BFS2023-04-18 20.逃离迷宫2023-04-11 21.[NOI1999] 生日蛋糕2023-03-28 22.数字三角形2023-03-28 23.Function2023-03-28 24.四色问题2023-03-25 25.P1036 [NOIP2002 普及组] 选数2023-03-25 26.小猫爬山思路2023-03-18 27.马的遍历2023-03-18 28.最少步数2023-04-25 29.[USACO07DEC]Mud Puddles S2023-04-27 30.非常可乐2023-04-27 31.前缀和2023-05-03 32.「USACO2016JAN」Subsequences Summing to Sevens2023-05-09 33.[NOIP2004 提高组] 津津的储蓄计划2023-05-11 34.[NOIP2016 普及组] 买铅笔2023-05-11 35.[NOIP2013 普及组] 计数问题2023-05-11 36.[NOIP2011 普及组] 数字反转2023-05-11 37.[NOIP2015 普及组] 金币2023-05-11 38.[NOIP2008 提高组] 笨小猴2023-05-11 39.[NOIP2007 普及组] 奖学金2023-05-11 40.[NOIP2003 普及组] 乒乓球2023-05-11 41. [NOIP2005 普及组] 陶陶摘苹果2023-05-11 42.[NOIP2009 普及组] 分数线划定2023-05-11 43.[NOIP2005 普及组] 校门外的树2023-05-11 44.[NOIP2018 普及组] 标题统计2023-05-11 45.[NOIP2004 普及组] 不高兴的津津2023-05-11 46.[NOIP2008 提高组] 火柴棒等式2023-05-11 47. [NOIP1998 普及组] 三连击2023-05-11 48. [USACO1.3]Ski Course Design2023-05-11 49.[NOIP2014 普及组] 珠心算测验2023-05-11 50.[NOIP2013 普及组] 表达式求值2023-05-11 51.数字三角形2023-05-13 52.「模板」最长不下降子序列 LIS2023-05-13 53.[NOIP2002 普及组] 过河卒2023-05-13

54. [NOIP1999 普及组] 导弹拦截2023-05-18

55.可回退的数字三角形2023-05-18 56.[NOIP2004 提高组] 合唱队形2023-05-18 57.动态规划部分PPT2023-05-24 58.【模板】01背包问题2023-05-27 59.所有背包问题模板2023-05-27 60.[NOIP2006 普及组] 开心的金明2023-05-27 61.【模板】完全背包问题2023-05-27 62.货币系统2023-05-27 63.小A点菜2023-05-30 64.最大约数和2023-05-30 65.NASA的食物计划2023-05-30 66.[USACO3.1]总分 Score Inflation2023-05-30 67.[NOIP2001 普及组] 装箱问题2023-05-30 68.[HAOI2012] 音量调节2023-06-01 69.[USACO08NOV]Buying Hay S2023-06-02 70.[USACO09MAR]Cow Frisbee Team S2023-06-02 71.编辑距离2023-06-03 72.2023-6-6 DP测试2023-06-06 73.租用游艇2023-06-10 74.石子合并（弱化版）2023-06-10 75.[USACO06FEB]Treats for the Cows G/S2023-06-13 76.排队接水2023-06-15 77.数列分段 Section I2023-06-17 78.[USACO1.3]混合牛奶 Mixing Milk2023-06-17 79.凌乱的yyy / 线段覆盖2023-06-17 80.独木桥2023-06-17 81.[NOIP2002 提高组] 均分纸牌2023-06-17 82.独木舟上的旅行2023-06-20 83.选择不相交区间2023-06-20 84.区间选点问题2023-06-20 85.最大数2023-07-01 86.区间覆盖问题2023-07-01 87.可分割背包问题2023-07-01 88.[COCI2011-2012#5] EKO / 砍树2023-07-01 89.【深基13.例1】查找2023-07-01 90.[NOIP2001 提高组] 一元三次方程求解2023-07-02 91.木材加工2023-07-02 92.[NOIP2015 提高组] 跳石头2023-07-02 93.数列分段 Section II2023-07-02 94.复制书稿2023-07-03 95.烦恼的高考志愿2023-07-03 96.银行贷款2023-07-03

[NOIP1999 普及组] 导弹拦截

题目描述

某国为了防御敌国的导弹袭击，发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。某天，雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段，所以只有一套系统，因此有可能不能拦截所有的导弹。

输入导弹依次飞来的高度，计算这套系统最多能拦截多少导弹，如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

输入格式

一行，若干个整数，中间由空格隔开。

输出格式

两行，每行一个整数，第一个数字表示这套系统最多能拦截多少导弹，第二个数字表示如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

样例 #1

样例输入 #1

 389 207 155 300 299 170 158 65

样例输出 #1

6
2

提示

对于前 $50\%$ 数据（NOIP 原题数据），满足导弹的个数不超过 $10^4$ 个。该部分数据总分共 $100$ 分。可使用 $\mathcal O(n^2)$ 做法通过。
对于后 $50\%$ 的数据，满足导弹的个数不超过 $10^5$ 个。该部分数据总分也为 $100$ 分。请使用 $\mathcal O(n\log n)$ 做法通过。

对于全部数据，满足导弹的高度为正整数，且不超过 $5\times 10^4$ 。

此外本题开启 spj，每点两问，按问给分。

$\text{upd 2022.8.24}$ ：新增加一组 Hack 数据。

解析

第一问

将拦截的导弹的高度提出来成为原高度序列的一个子序列，根据题意这个子序列中的元素是单调不增的（即后一项总是不大于前一项），我们称为单调不升子序列。本问所求能拦截到的最多的导弹，即求最长的单调不升子序列。

考虑记 $dp_{i}$ 表示「对于前 $i$ 个数，在选择第 $i$ 个数的情况下，得到的单调不升子序列的长度最长是多少」。于是可以分两种情况：

第 $i$ 个数是子序列的第一项。则 $\mathit{dp}_i\gets 1$ 。
第 $i$ 个数不是子序列的第一项。选择的第 $i$ 个数之前选择了第 $j$ 个数。根据题意，第 $j$ 个数的值 $h(j)$ 应当小于第 $i$ 个数的值 $h(i)$ 。枚举这样的 $j$ ，可以得到状态转移方程：

{d p}_{i} = max_{j < i, h (j) \geq h (i)} {d p_{j} + 1}

$\mathit{dp}_i=\max_{j<i,h(j)\ge h(i)} \{\mathit{dp_j}+1\}$

综合这两种情况，得到最终的状态转移方程：

{d p}_{i} = max {1, max_{j < i, h (j) \geq h (i)} {{d p}_{j} + 1}}

$\mathit{dp}_i=\max\{1,\max_{j<i,h(j)\ge h(i)}\{\mathit{dp}_j+1\}\}$

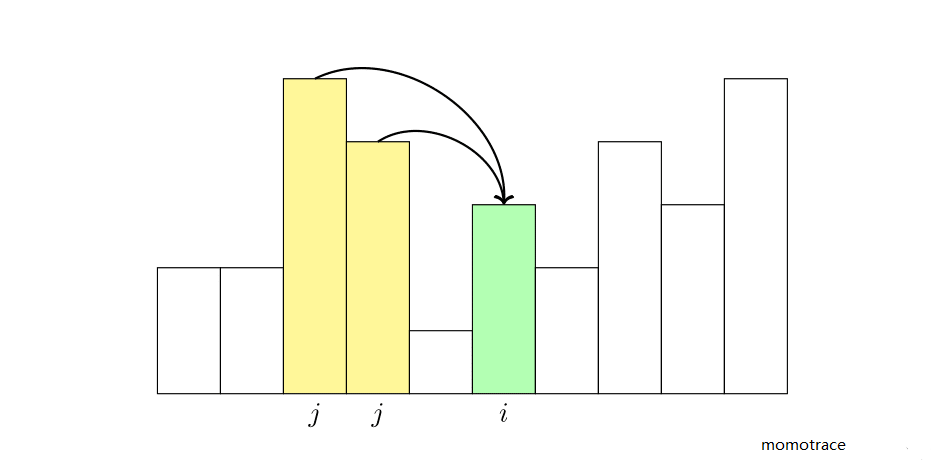
值得注意的是，第 $n$ 个数不一定是最长单调不升子序列的最后一项。为了求出答案，我们需要枚举最后一项是哪个：

a n s = max_{1 \leq i \leq n} {{d p}_{i}}

$\mathit{ans}=\max_{1\le i\le n}\{\mathit{dp}_i\}$

直接枚举进行状态转移，时间复杂度显然是 $\mathcal O(n^2)$ 。下面考虑优化。

记 $f_i$ 表示「对于所有长度为 $i$ 的单调不升子序列，它的最后一项的大小」的最大值。特别地，若不存在则 $f_i=0$ 。下面证明：

随 $i$ 增大， $f_i$ 单调不增。即 $f_i\ge f_{i+1}$ 。

考虑使用反证法。假设存在 $u<v$ ，满足 $f_u<f_v$ 。考虑长度为 $v$ 的单调不升子序列，根据定义它以 $f_v$ 结尾。显然我们可以从该序列中挑选出一个长度为 $u$ 的单调不升子序列，它的结尾同样是 $f_v$ 。那么由于 $f_v>f_u$ ，与 $f_u$ 最大相矛盾，得出矛盾。

因此 $f_i$ 应该是单调不增的。

现在考虑以 $i$ 结尾的单调不升子序列的长度的最大值 $\mathit{dp}_i$ 。由于我们需要计算所有满足 $h(j)>h(i)$ 的 $j$ 中， $\mathit{dp}_j$ 的最大值，不妨考虑这个 $\mathit{dp}_j$ 的值是啥。设 $\mathit{dp}_j=x$ ，那么如果 $h(i)> f_x$ ，由于 $f_x\ge h(j)$ ，就有 $h(i)>h(j)$ ，矛盾，因此总有 $h(i)\le f_x$ 。

根据刚刚得出的结论， $f_i$ 单调不增，因此我们要找到尽可能大的 $x$ 满足 $h(i)\le f_x$ 。考虑二分。

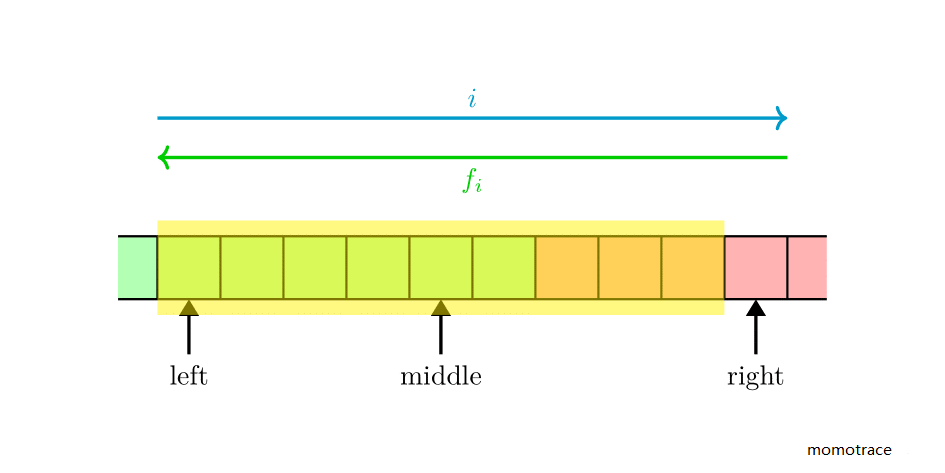
绿色区域表示合法的 $f_x$ （即 $f_x\ge h(i)$ ），红色区域表示不合法的 $f_x$ （即 $f_x< h(i)$ ），我们需要找到红绿之间的交界点。

假设二分区域为 $[l,r)$ （注意开闭区间。图上黄色区域标出来了二分区域内实际有效的元素）。每次取 $m=\frac{l+r}{2}$ ，如果 $f_m$ 在绿色区域内，我们就把 $l$ 移动到此处（ $l\gets m$ ）；否则把 $r$ 移动到此处（ $r\gets m$ ）。

当 $r-l=1$ 时， $l$ 处位置即为我们需要找的位置。转移 $\mathit{dp}_i\gets l+1$ 即可。记得更新 $f$ 。但是我们只用更新 $f_{\mathit{dp}_i}$ ，这是因为 $f_1,f_2,\cdots f_{\mathit{dp_i}-1}$ 的大小肯定都是不小于 $h(i)$ 的。 $f_{\mathit{dp}_i}$ 是最后一个不小于 $h(i)$ 的位置， $f_{\mathit{dp}_i+1}$ 则小于 $h(i)$ 。

时间复杂度 $\mathcal O(n\log n)$ ，可以通过该问。

第二问

考虑贪心。

从左到右依次枚举每个导弹。假设现在有若干个导弹拦截系统可以拦截它，那么我们肯定选择这些系统当中位置最低的那一个。如果不存在任何一个导弹拦截系统可以拦截它，那我们只能新加一个系统了。

假设枚举到第 $i$ 个导弹时，有 $m$ 个系统。我们把这些系统的高度按照从小到大排列，依次记为 $g_1,g_2,\cdots g_m$ 。容易发现我们就是要找到最小的 $g_x$ 满足 $g_x\ge h_i$ （与第一问相同，这是可以二分得到的），然后更新 $g_x$ 的值。更新之后， $g_1,g_2\cdots g_x$ 显然还是单调不增的，因此不用重新排序；如果找不到符合要求的导弹拦截系统，那就说明 $g_m<h_i$ ，直接在后头增加一个就行。

时间复杂度 $\mathcal O(n\log n)$ ，可以通过该问。

Code

注：本蒟蒻能力有限，无法AC，谅解一下啦

Method 1

 #include<bits/stdc++.h>
using namespace std;
int a[1010],f[1010],b[1010],n,cnt=1,xt[1010];
bool pd[1010];
int main()
{
	while(cin>>a[++n]) f[n]=1;
	n--;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<i;j++)
		{
			if(a[j]>=a[i])
			{
				f[i]=max(f[i],f[j]+1);
			}
		}
	}
	int ans=-1;
	for(int i=1;i<=n;i++)ans=max(ans,f[i]);
	b[1]=a[1];
	for(int i=2;i<=n;i++)
	{
		int minn=30010,x=-1;
		for(int j=1;j<=cnt;j++)
		{
			if(b[j]>=a[i])
			{
				if(b[j]<minn)
				{
					x=j;
					minn=b[j];
				}
			}
		}
		if(x==-1)b[++cnt]=a[i];
		else b[x]=a[i];
	}
	cout<<ans<<'\n'<<cnt;
	return 0;
}

Method 2

 #include <bits/stdc++.h>
using namespace std;
 
int a[0xffffff], x, l, dp[0xffffff], maxn;
int g[0xffffff], cnt;
 
int main()
{
	while(cin >> x) 
	{
		a[++l] = x;
	}
	for(int i=1;i<=l;i++)
	{
		int k=1;
		while(k<=cnt && g[k]>=a[i]) 
		{
			k++;
		}
		if(k>cnt) 
		{
			g[++cnt]=a[i];
		}
		else g[k] = a[i];
	}
	cout << cnt << endl;
	cnt=0;
	for(int i=1;i<=l;i++)
	{
		int k = 1;
		while(k<=cnt && g[k]<a[i])
		{
			k++;
		}
		if(k>cnt) 
		{
			g[++cnt] = a[i];
		}
		else g[k] = a[i];
	}
	cout << cnt << endl;
}

观察第二问的代码，与第一问进行比较，可以发现这段代码等价于计算最长上升子序列（严格上升，即后一项大于前一项）。这其实是 $\text{Dilworth}$ 定理（将一个序列剖成若干个单调不升子序列的最小个数等于该序列最长上升子序列的个数），本处从代码角度证明了该结论。

上一篇My imperial harem or seraglio [password:原神's English]（bushi

下一篇可回退的数字三角形

posted @ 2023-05-18 20:44 Momo·Trace 阅读(86) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

MT默哥的博客

Not just a blog.

[NOIP1999 普及组] 导弹拦截

[NOIP1999 普及组] 导弹拦截

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

提示

解析

第一问

第二问

Code

Method 1

Method 2

公告

合集

随笔分类

随笔档案

文章分类

相册

阅读排行榜

评论排行榜

最新评论

🍺

hello!这里是留言板！欢迎大家留言！！！

	#include<bits/stdc++.h>
	using namespace std;
	int a[1010],f[1010],b[1010],n,cnt=1,xt[1010];
	bool pd[1010];
	int main()
	{
	while(cin>>a[++n]) f[n]=1;
	n--;
	for(int i=1;i<=n;i++)
	{
	for(int j=1;j<i;j++)
	{
	if(a[j]>=a[i])
	{
	f[i]=max(f[i],f[j]+1);
	}
	}
	}
	int ans=-1;
	for(int i=1;i<=n;i++)ans=max(ans,f[i]);
	b[1]=a[1];
	for(int i=2;i<=n;i++)
	{
	int minn=30010,x=-1;
	for(int j=1;j<=cnt;j++)
	{
	if(b[j]>=a[i])
	{
	if(b[j]<minn)
	{
	x=j;
	minn=b[j];
	}
	}
	}
	if(x==-1)b[++cnt]=a[i];
	else b[x]=a[i];
	}
	cout<<ans<<'\n'<<cnt;
	return 0;
	}

	#include <bits/stdc++.h>
	using namespace std;

	int a[0xffffff], x, l, dp[0xffffff], maxn;
	int g[0xffffff], cnt;

	int main()
	{
	while(cin >> x)
	{
	a[++l] = x;
	}
	for(int i=1;i<=l;i++)
	{
	int k=1;
	while(k<=cnt && g[k]>=a[i])
	{
	k++;
	}
	if(k>cnt)
	{
	g[++cnt]=a[i];
	}
	else g[k] = a[i];
	}
	cout << cnt << endl;
	cnt=0;
	for(int i=1;i<=l;i++)
	{
	int k = 1;
	while(k<=cnt && g[k]<a[i])
	{
	k++;
	}
	if(k>cnt)
	{
	g[++cnt] = a[i];
	}
	else g[k] = a[i];
	}
	cout << cnt << endl;
	}