前缀和

前缀和

一、介绍

前缀，顾名思义就是一个东西前面的点缀...（bushi

其实打比方来说就是：假如有一字符串ABCD，那么他的前缀就是A、AB、ABC、ABCD这四个从新从第一个字母一次往后开始拼接的字符串。当然这是字符串。但前缀和一般应用于数组，对于给定的数组a=[1,2,3,4]，他的前 i 项和sum[i]就表示数组中a[0]~a[i]的和，具体为：
sum[0]=a[0]
sum[1]=a[0]+a[1]
......
sum[i]=sum[0]+sum[1]+...+sum[i];

二、定义

定义：前缀和是指某一序列的前 n 项和。

基于前缀和的使用，我们一般把前缀和分为一维前缀和和二维前缀和。

三、一维前缀和

定义

基于一维数组的前缀和就是原数组前n个元素的和。

const int N = 10010;
 
int a[N]; //原数组a[]
int s[N]; //前缀和数组s[]
 
//根据定义 一维前缀和s[i]
s[i] = a[1] + a[2] + a[3] +...+ a[i];
 
//举例 设i=3 根据上式可得
s[3] = a[1] + a[2] + a[3];
 
//根据上面举例，可以再一步写成
s[i] = s[i-1] + a[i]; 

需要注意的一点是：数组的下标都是从 1 开始的！！！

作用

主要作用是可以在O(1)时间情况下快速的求出任一区间[l,r]内的元素之和。

//例如求a[3]+...+a[10]之间的和，我们可以利用前缀和迅速求出：
  a[3]+...+a[10]
= (a[1]+a[2]+a[3]...+a[10]) - (a[1]+a[2])
= s[10] - s[2]
 
//根据上面举例,我们可以推导出求某一区间[l,r]内的和的公式
  a[l]+a[l+1]+...+a[r-1]+a[r] 
= s[r] - s[l-1];

方法

一维数组求前缀和方法

int a[100],s[100];
for(int i = 1; i<= 99; i++)
{
    scanf("%d",&a[i]);
}
for(int i = 1; i<= 99; i++)
{
    s[i] = s[i-1]+a[i];
}

实战演练！！！

「模板」前缀和

输入n个数，给出m个询问，询问区间[x,y]的和。

输入

• 第一行为n和m，1<=n,m<=100000

• 接下来一行为n个数，范围在0~100000之间

• 接下来m行，每行两个数x,y，输出第x个数到第y个数之间所有数的和。保证x<=y

输出

m个输出

样例输入

5 3
1 2 0 7 6
1 3
2 2
4 5

样例输出

3
2
13

代码：

#include <bits/stdc++.h>
using namespace std;
int n,m;
long long a[100010],b[100010];//见注释1
int main()
{
	cin >> n >> m;
	for(int i=1; i<=n;i++)
	{
		cin >> a[i];
	}
	b[0]=0;
	for(int i=1;i<=n;i++)
	{
		b[i]=b[i-1]+a[i];
	}
	while(m--)
	{
		int l,r;
		cin >> l >> r;
		cout << b[r] - b[l-1] << "\n";
	}
	return 0;
}

注释①：测试范围大

四、二维前缀和

定义

基于二维数组的前缀和，它是指一个前 i 行和前 j 列的子矩阵的和

const int N =100010;
int a[N][N] //原二维数组
int s[N][N] //二维前缀和数组
 
//根据定义可得
s[i][j] = a[1][1] + a[1][2] + ... + a[1][j]+
          a[2][1] + 1[2][2] + ... + 1[2][j]+
          a[3][1] +   ...   + ... + a[3][j]+
             +                         +
            ....                      ....
             +                         + 
          a[i][1] +   ...   + ... + a[i][j]

作用

主要作用是可以在是可以在O(1)情况下求出任何子矩阵的和

图解：

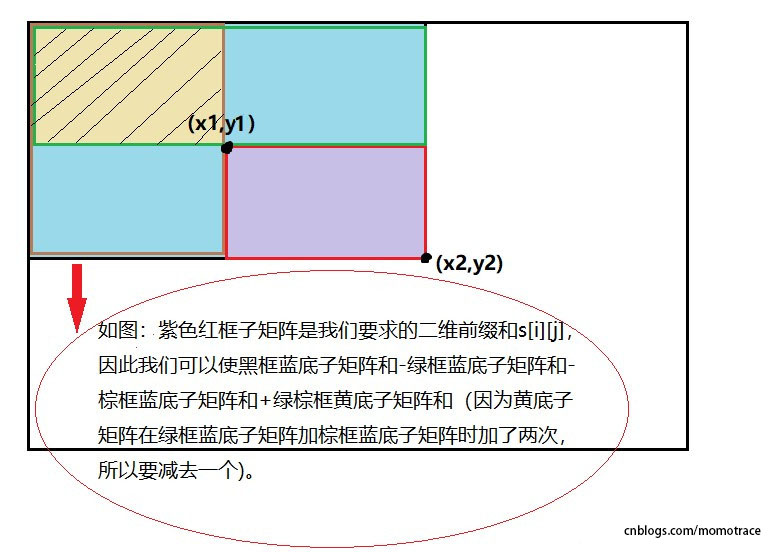
在这个矩阵（二维数组）中，我们要求上图中紫色区域的和，现在我们已经预处理出了所有点的前缀和，现在给定两个点\(（x1,y1）\)，\(（x2,y2）\)，我们需要求的是以这两个点连线为对角线的一个子矩阵的数值之和。首先我们可以把\(s[x2][y2]\)求出来，它代表整个大矩形的前缀和，然后我们分别减去它右边多出来的一块的前缀和和上边多出来一块的前缀和，但是需要注意下边的左上角被减了两次，所以我们需要加回来一次。故对于一次的查询是\(s[i][j]\)应该等于\(s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]\)。

• 所求子矩阵和=\(s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]\);

方法

二维数组求前缀和方法

const int N = 10010;
int a[N][N],s[N][N]
//n,m为键盘输入
for(int i = 1; i <= n; i++)
{
    for(int j = 1;j <= m; j++)
    {
       scanf("%d",&a[i][j]);
    }
}
for(int i = 1; i<= n; i++)
{
    for(int j = 1; j <= m; j++)
    {
       s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + a[i][j];
    }
}

具体代码！！！

#include <iostream>
 
const int N = 1010;
int n,m,q;
int a[N][N],s[N][N];
 
int main()
{
    scanf("%d%d%d",&n,&m,&q);
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1;j <= m; j++)
        {
            scanf("%d",&a[i][j]);
        }
    }
    for(int i = 1; i<= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + a[i][j];
        }
    }
    while(q--)
    {
        int x1,y1,x2,y2,re;
        scanf("%d%d%d%d",&x1,&y2,&x2,&y2);
        re = s[x2][y2] - s[x1-1][y2] - s[x2][y1-1] + s[x1-1][y1-1];
        printf("%d\n",re);
    }
}