统计学三：线性回归

 

 

线性回归是一种重要的统计方法，在学术研究以及生产实践中，都有着广泛的应用。本课节将从实践角度出发，将模型的构建、模型的评价和注意事项娓娓道来。通过学习，学员将完全掌握线性回归的核心原理与真实应用。

本节课涵盖的知识点有：

• 拟合优度
• 回归方程的显著性检验
• 回归系数的显著性检验

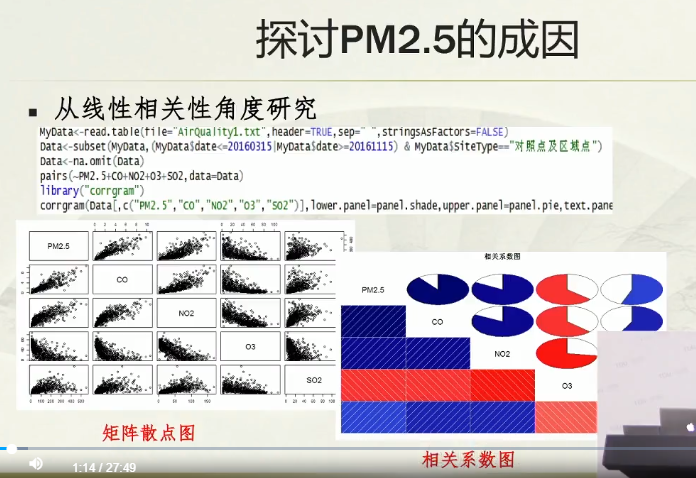
默认是线性相关；

假定成因是线性关系而得出的线性模型；

几个变量就是几元回归模型，上述为四元回归模型；

为了估计β值，于是将回归模型转为回归方程；

回归方程中的β参数代表当前几维超平面的截距、斜率等；

是某一个点的估计值；

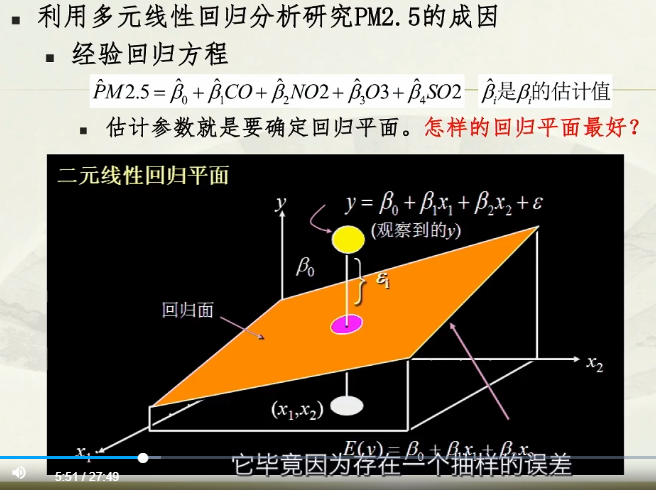
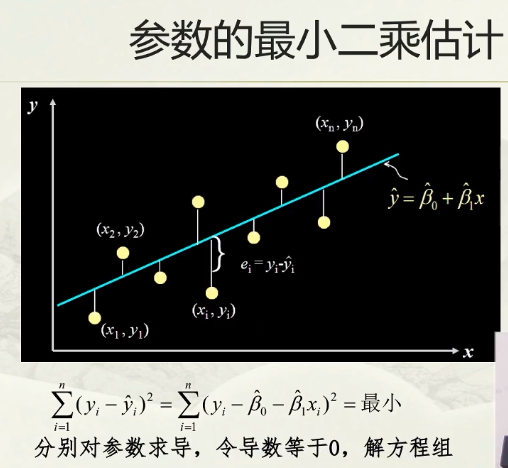
散点图：两两变量之间的关系；—— 可以看出影响因素之间的关系，但是影响的程度看不出；

 

验证模型的合理性：

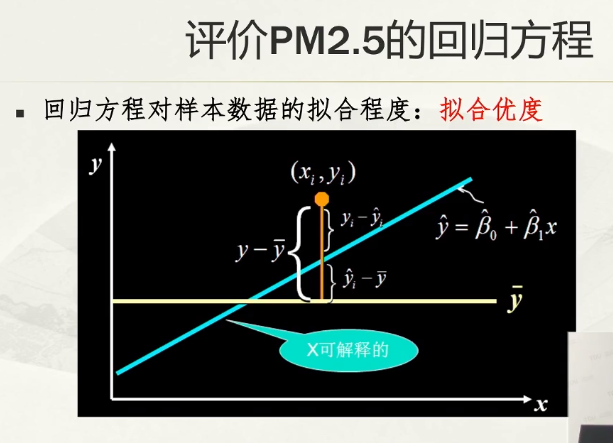
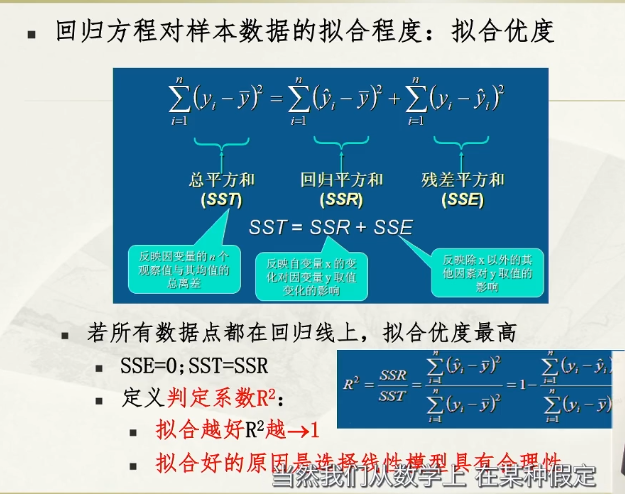
拟合值在0.7几/0.8几就说明拟合度不错；

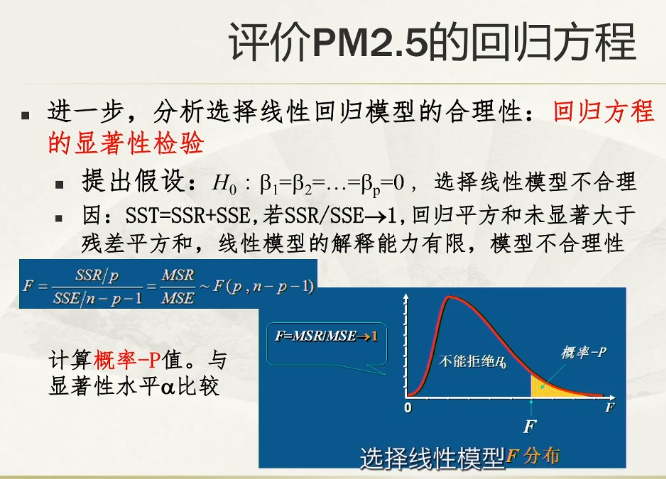
上图为F分布；

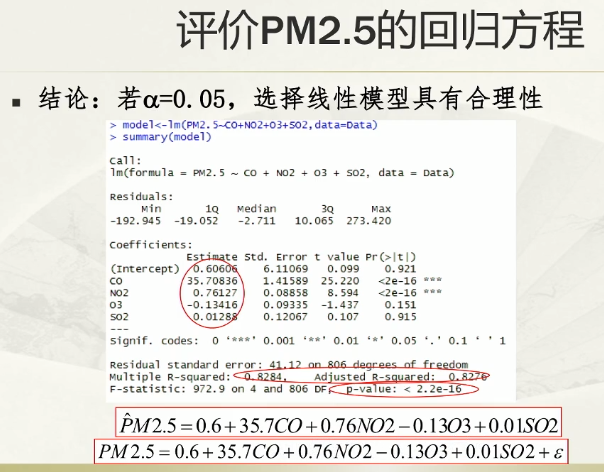
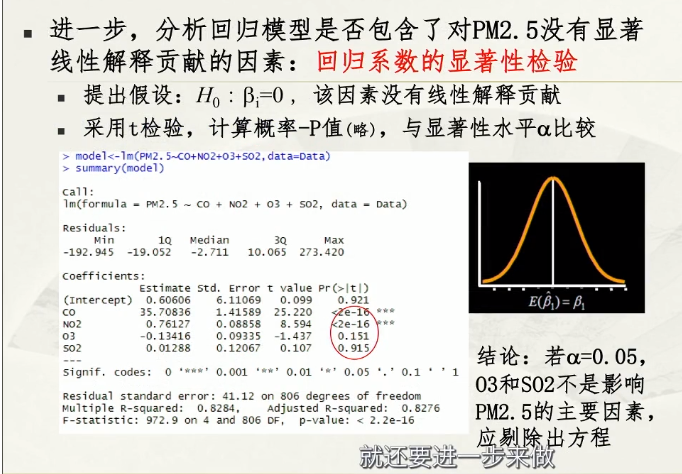
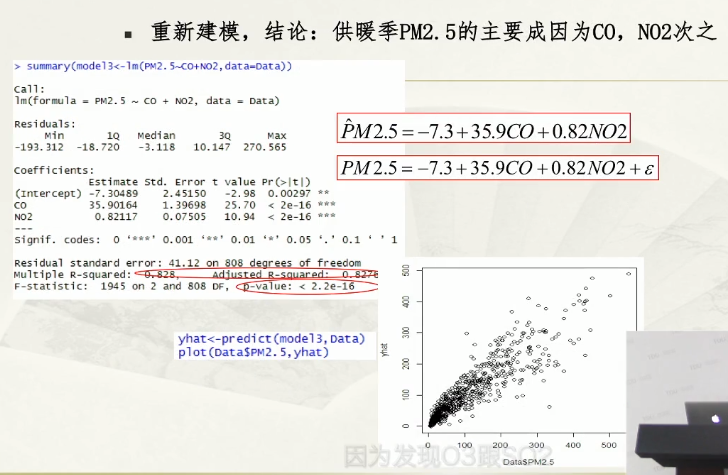
拟合度越不错，线性相关的样本分布越倾向于45°角线上；

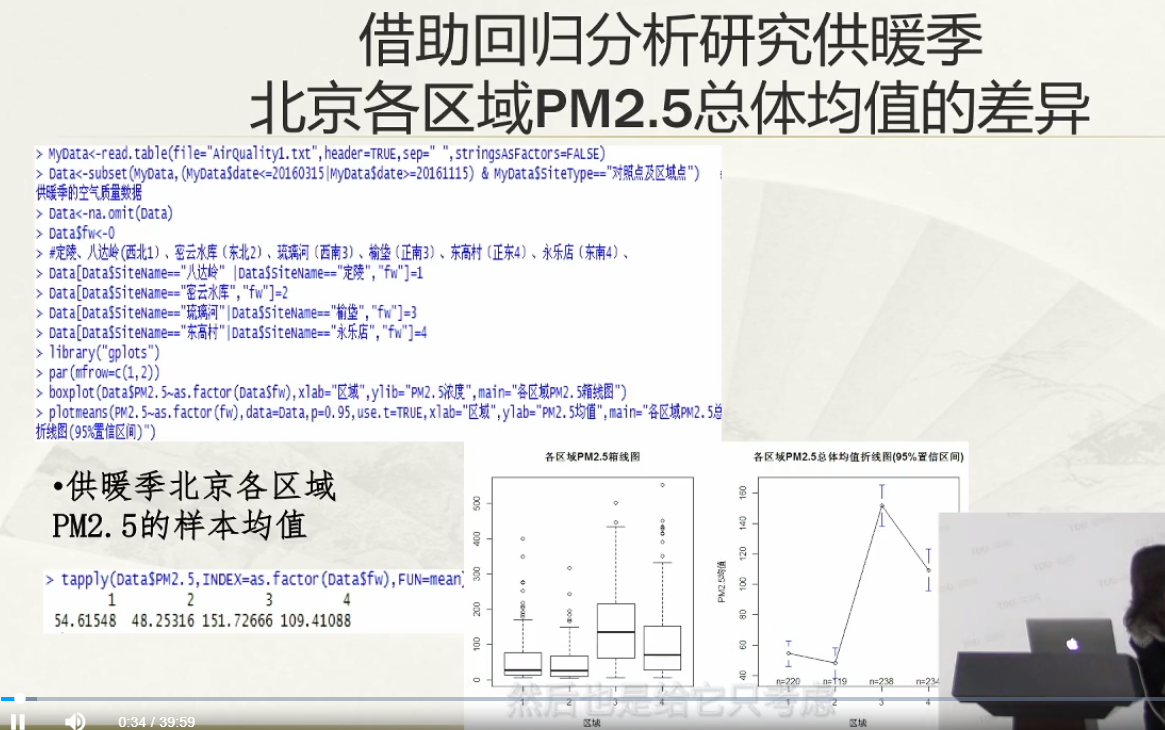
当解释变量是分类型变量时，需要把自变量变成虚拟自变量，即变成只有0和1代表的变量。

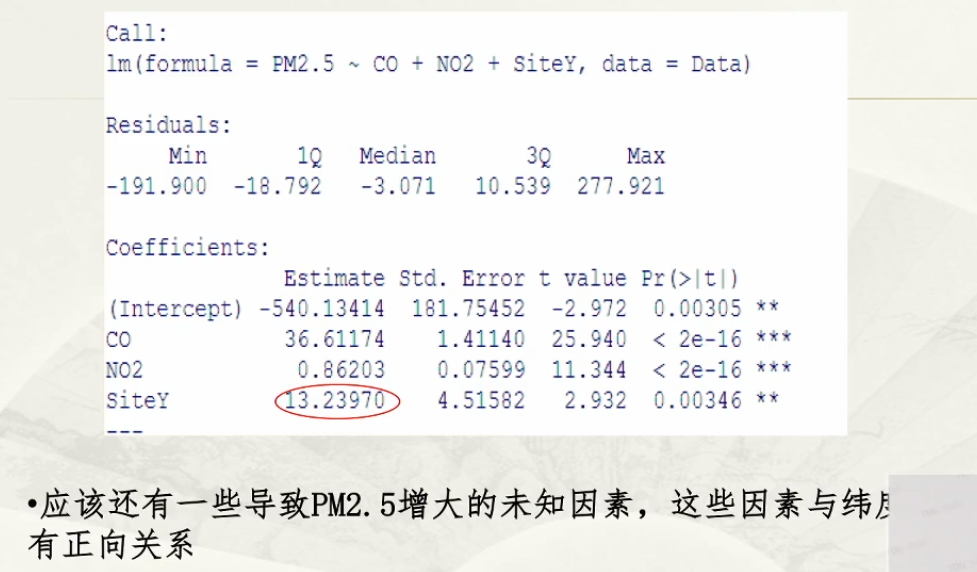
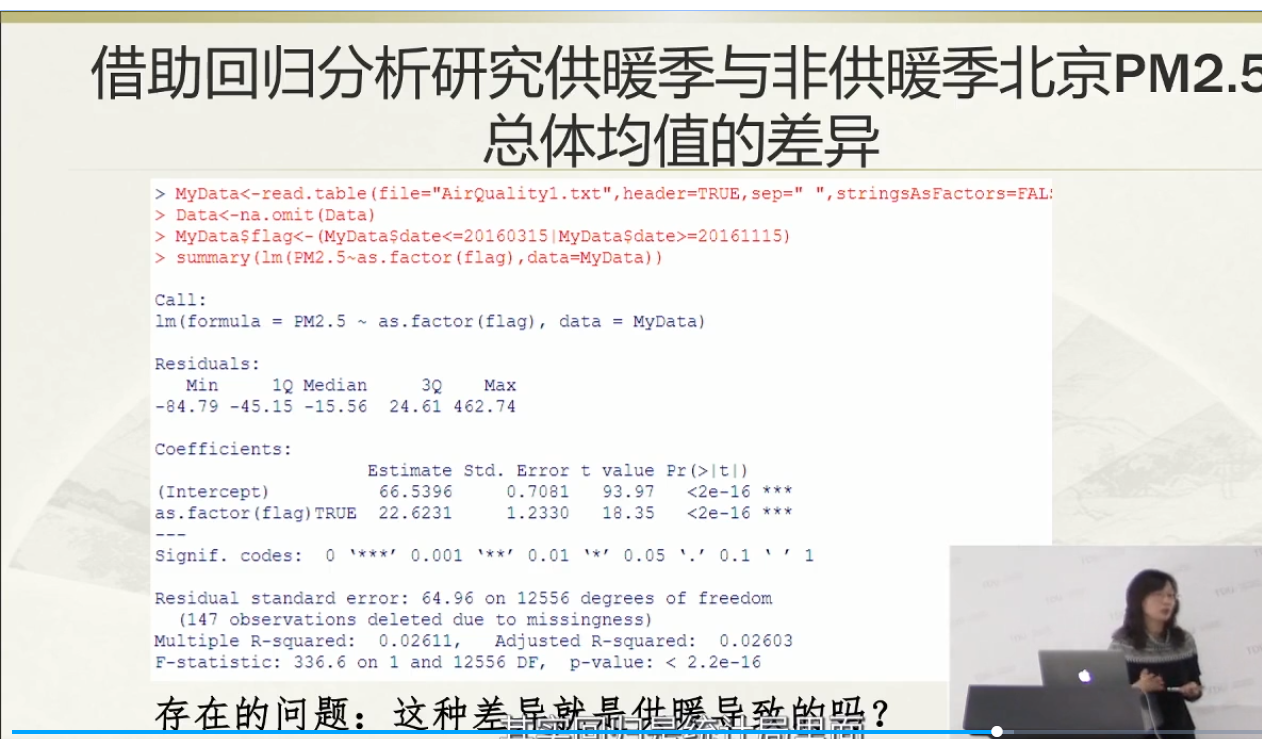
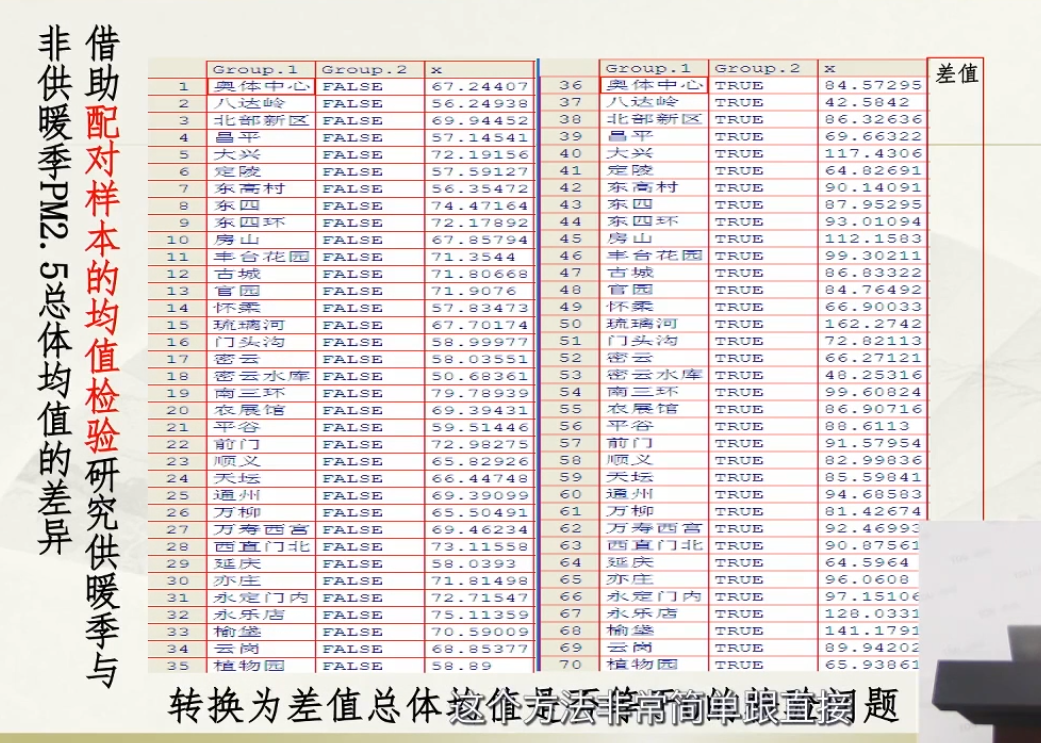
配对样本的均衡检验：