一. 数据种类:
不可测量的数据+可测量的数据;
| |
分类数据 数值数据
-
分类数据:数值数据之间并非相等间隔(比如天气,柔道段位等);
-
数值数据:数值数据之间有相等间隔(比如身高,体重,气温等);
二. 数据整体的状态(数值数据):
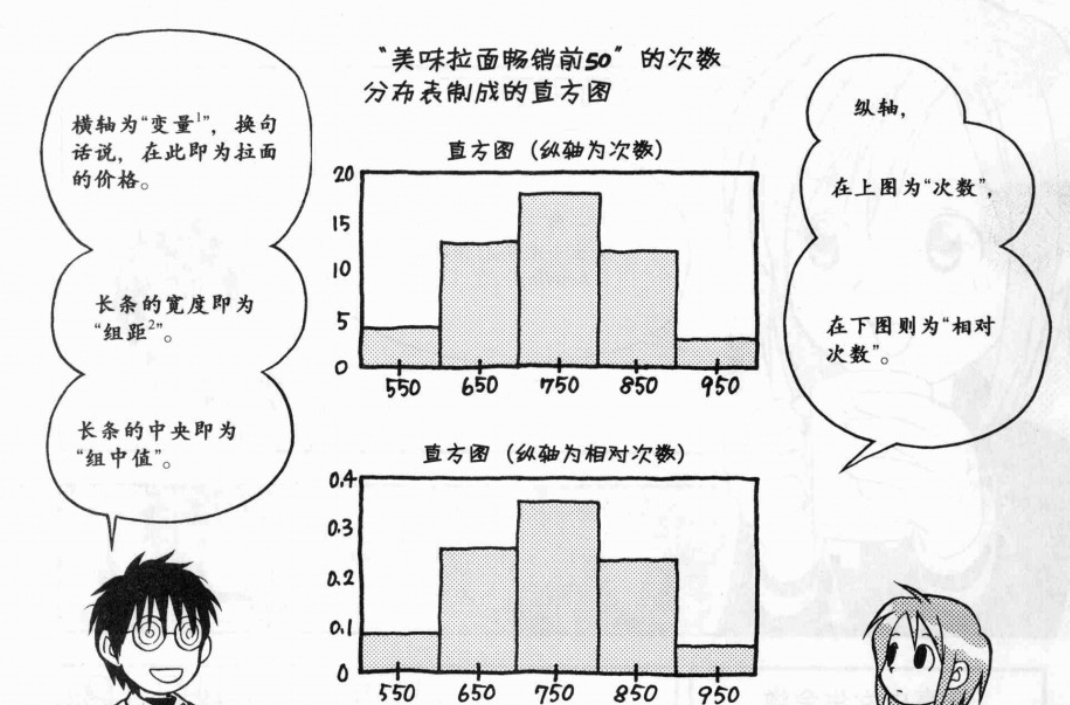
1. 次数分布表和直方图;组中值(中间值)、次数、相对次数(所属各组的数值/所有数值);
2. 平均数:算术平均数(即均值,总和/数量)、几何平均数( )、调和平均数(
)、调和平均数(  );
);
3. 中位数:将数据依大小顺序排列时,最中间的值(当有异常大或者异常小的值时);
4. 标准差:表示一组数据平均离散程度的指标;标准差的最小值为0,而数据的离散程度越大,标准差的值就越大;

总体标准差=

; 样本标准差=

5. 次数分布表的组距:
次数分布表:下表中的组距设为100;组距以分析者能接受的组距处理即可;
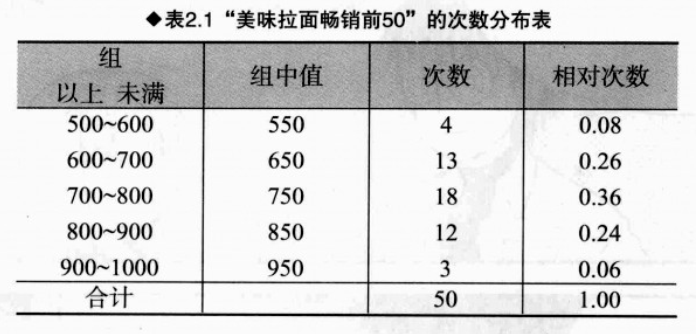
可使用史特吉斯公式: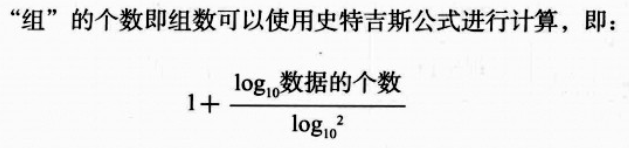
组距:
6. 推断统计学和描述统计学:
(1)推断统计学:从样本的信息推测整体状况;
(2)描述统计学:借由整理资料,尽可能简单明了地显示出整体状况为目的的统计学,即将对象集合视为一个总体的统计学;
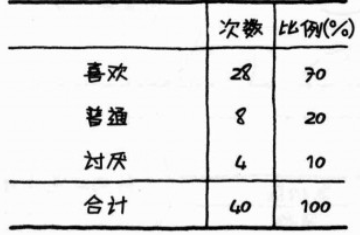
三. 数据整体的状态(分类数据):
次数分布表:
四. 标准计分和离差:
1. 标准化:以距离平均数的远近状况及资料的“离散程度”作为基础,将数据的价值转换为易于讨论的数据;
2. 标准计分: (每一数据-平均数)/标准差
(每一数据-平均数)/标准差
3. 标准计分的特征:
(1)无论作为变量的满分为几,其标准计分的平均数势必为0,而标准计分的标准差势必为1;(满分为100分的考试和满分为200分的考试也可以比较)
(2)无论作为变量的单位是什么,其标准计分的平均数势必为0,而标准计分的标准差势必为1;(安打率和全垒打数等即使单位不同也可以进行比较)
4. 离差:离差=标准计分*10+50;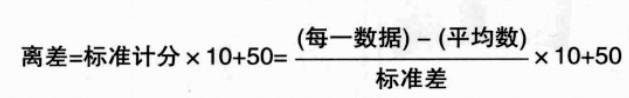
(1)无论作为变量的满分为几,其离差的平均数势必为50,而标准计分的标准差势必为10;
(2)无论作为变量的单位是什么,其标准计分的平均数势必为50,而标准计分的标准差势必为10;

五. 求机率:
1. 机率密度函数:直方图中,将距离缩小至极限后,所得之曲线的公式,在统计学上称为:机率密度函数。
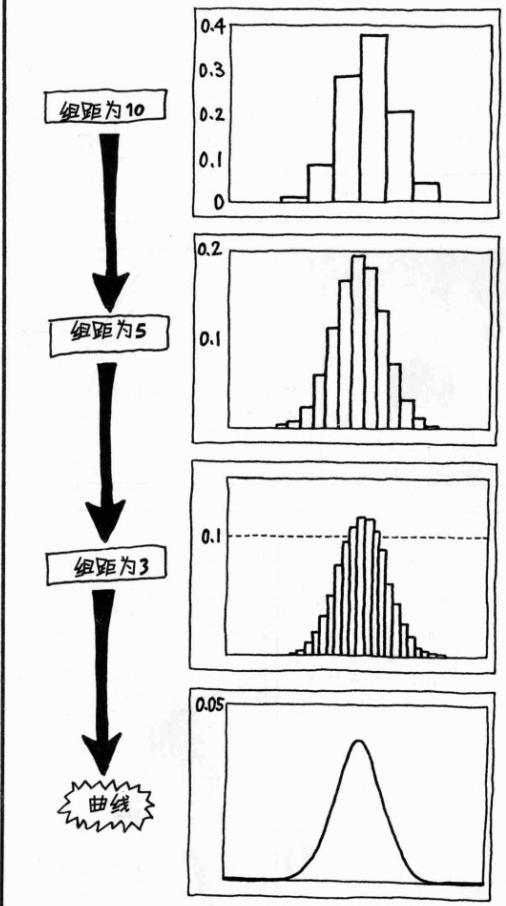
2. 正态分布:

特征:(1)以平均值为中心呈左右对称(2)受到平均值和标准差的影响
统计学中,将x的机率密度函数符合上述公式的,以“x服从平均值为OO,标准值为XX的正态分布”来表示。
3. 标准正态分布:
(1)将初始数据进行标准化(计算出每条数据的标准计分),对一系列标准计分的数据用正态分布的图表示出来;

(2)所有标准正态分布之机率密度函数的图形和横轴所围成的面积都是1;
(3)标准正态分布的图形和横轴围成的面积,与其比例及其机率都是相同的;

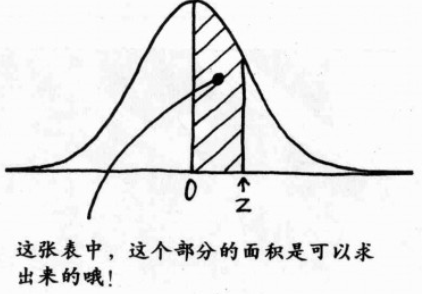
可以查到的面积指中间对称轴与至之间的面积;
4. 卡方分布:
(1)
(2)卡方:自由度,类似 f(x) = ax + b 中的斜率 a,会影响图像形状的数值;
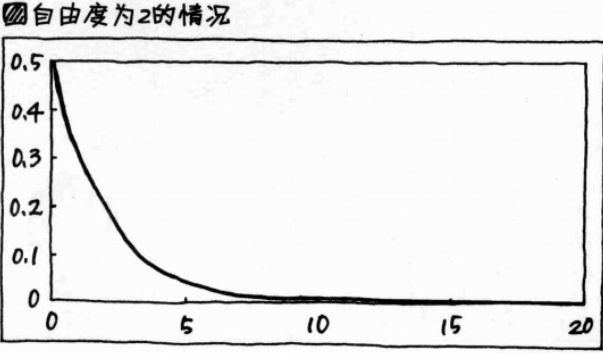
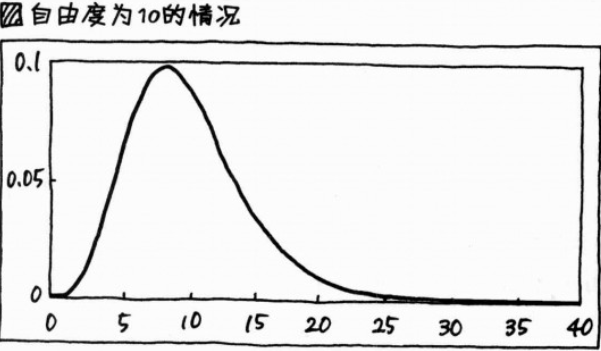
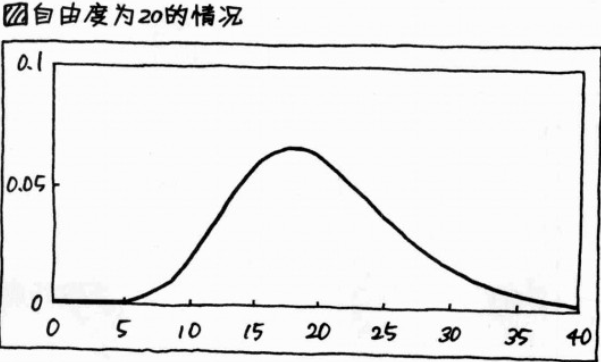
(3)卡方分布表:记录了对应这个部分的机率(=面积=比例)P的横轴刻度 x²(即卡方)之值的表;类似于正态分布表;
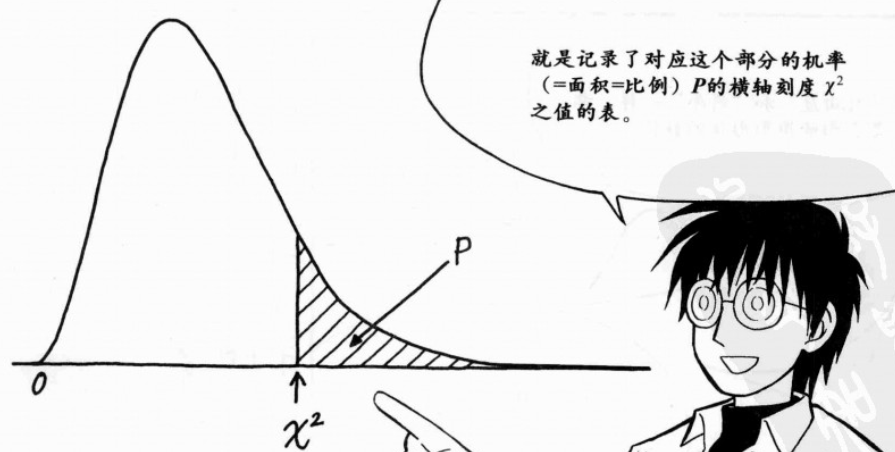
标准正态分布表为记录对应横轴的刻度之机率的表;
卡方分布表则记录对应机率之横轴刻度的表;
5. t分布:

6. F 分布:

7. Excel:
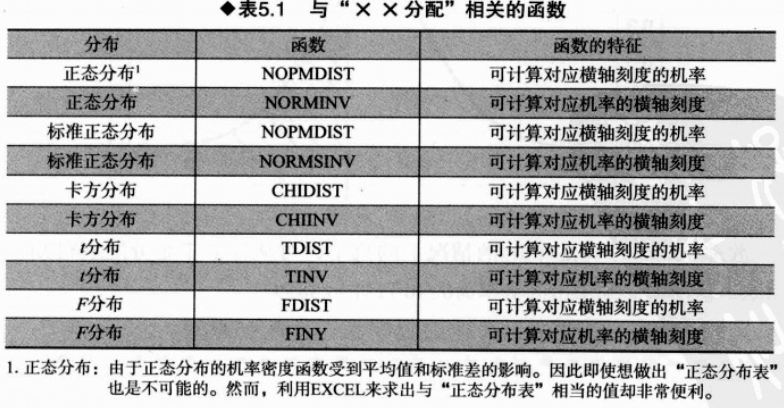
六. 双变量的相关分析:(各自计算步骤书中自查)
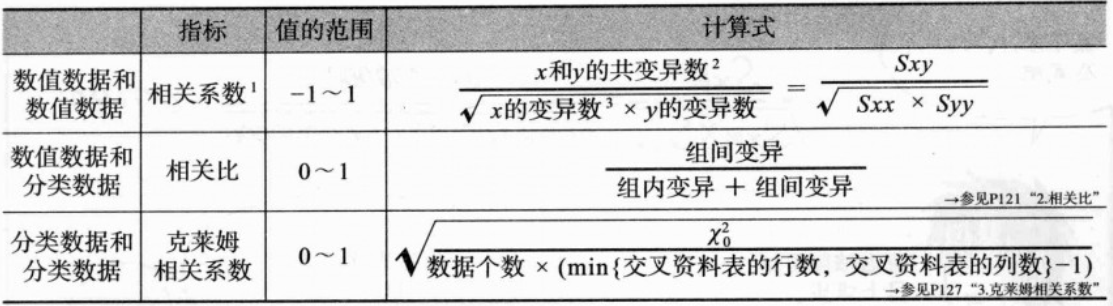
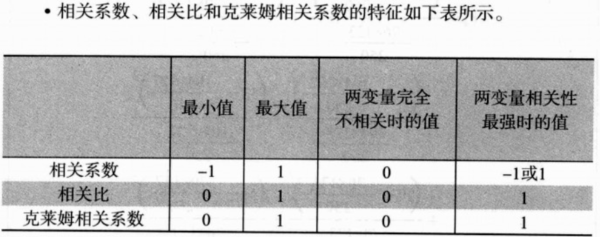
1. 相关系数:为清楚表示数值数据与数值数据之间是否具有“直线性”关联的指标。
(1)若两个变量的相关性越强,则相关系数就会越接近1;如果关联性越弱,相关系数则会越接近0。
(2)相关系数的若为正值,则称为“正相关”;反之,若为负值,则称为“负相关”;若为0,则称为“不相关”。
但是,关于相关系数的值,在统计学上,“若其值在XX以上则可说两个变量关联性较强”的基准是不存在的。
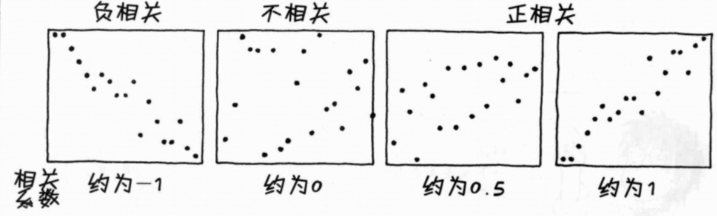
(3)

2. 相关比:数值数据和分类数据;相关比值的范围介于0~1之间;两个变量的关联性越强,则相关比的值就会越接近1;越弱,越接近0。

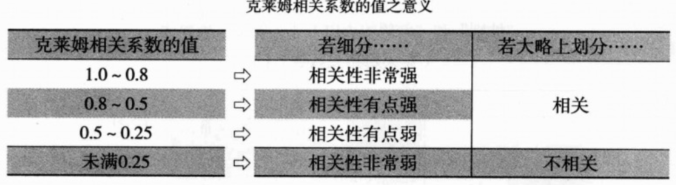
3. 克莱姆相关系数:分类数据和分类数据之间相关程度得指标;也可称为“克莱姆得关联系数”、“克莱姆V”或“独立系数”。
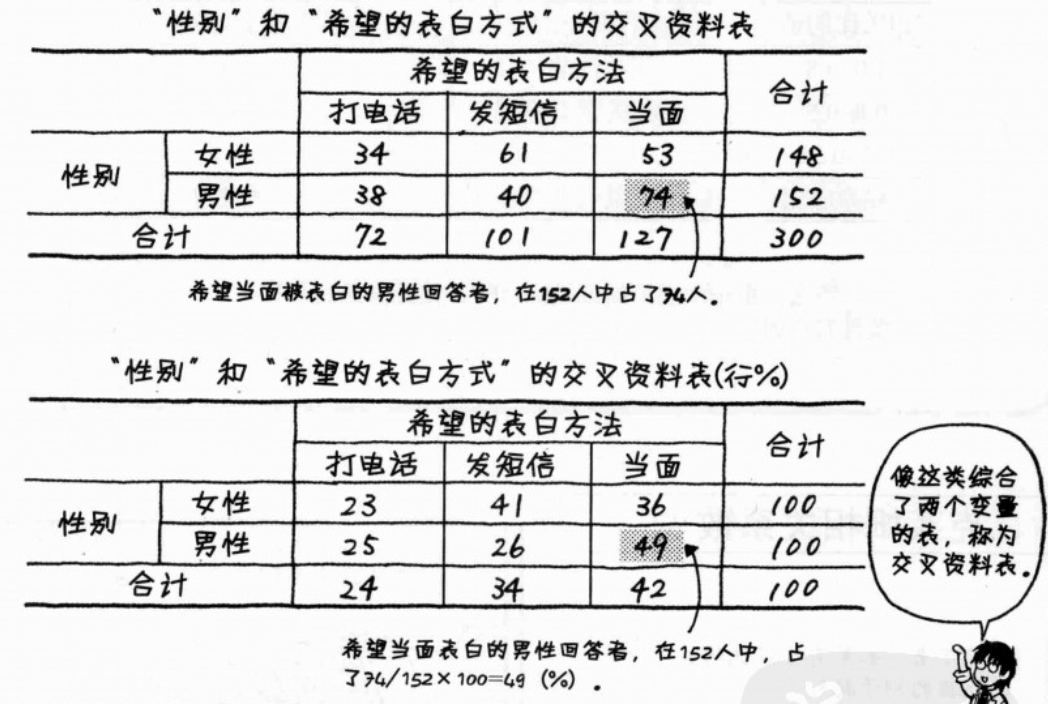
皮尔森卡方统计量即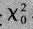 可以根据公式算出,具体方法自查。
可以根据公式算出,具体方法自查。
观测次数和期望次数得差异越大,两类数据之间得关联程度越强,皮尔森的卡方统计量
![]()

也会越大。
克莱姆相关系数的值介于0与1之间,两个变量的关联性越强,则此值越接近1,反之,则会越接近0。
七. 独立性检验:
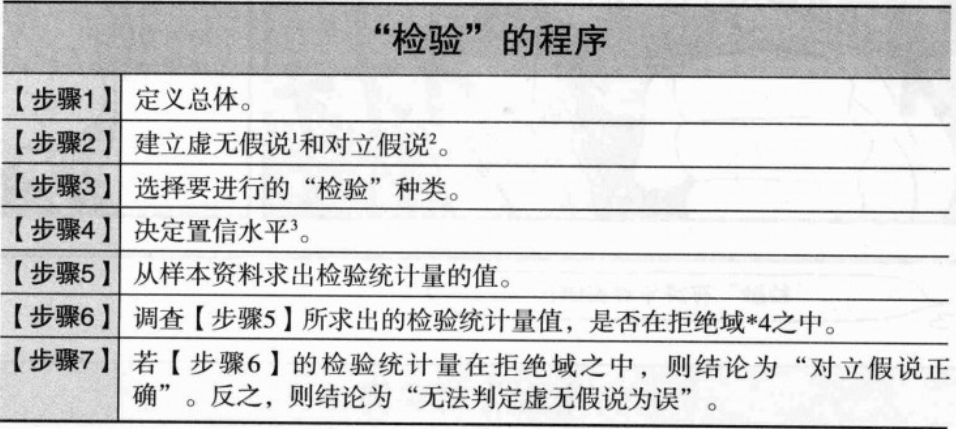
1. 什么是检验:由样本数据来推测分析者针对总体所建立的假说是否正确的分析方法。"检验"这个名词,正确说来,应该称为“统计的假说检验”。

2. 检验的种类多,但步骤都是一样的。
附:
(1)主体:总体是由分析者决定。比如设定“居住在都市的有选举权者”和“居住在农村的有选举权者”为总体,那么,“都市”具体指哪里呢,是“东京都”还是“各都道府县的地方政府所在地”,这是由分析者决定的;
(2)虚无假说和对立假说见下方;
(3)检验种类:分析者决定,选择符合分析目的的检验。独立性检验/相关比检验/无相关检验等五个;
(4)置信水平:分析者决定置信水平。置信水平一般设为0.05或0.01,通常以 α 符号表示;
(5)求出检验统计量的值:检验统计量是指将样本资料转换为1个值的公式。检验种类不同,检验统计量也会不同,若是独立性检验,检验统计量为皮尔森的卡方统计量
![]()

;若是无相关检验,则是

(6)拒绝域:拒绝域依置信水平α不同而变化。为对应置信水平的范围。

(7)若检验统计量值在拒绝域之中,则结论为“对立假说正确”,反之,则结论为“无法判定虚无假说为误”。检验统计量的值即使在拒绝域中,单以“检验”并无法给出“对立假说绝对正确,但是,只能作虚无假说存在正确的机率。其值最大为(α*100%)“的结论。
3. 独立性检验:推测“总体的克莱姆相关系数的值是否为0”的分析方法,换句话说,就是推测“交叉资料表中的两变量是否相关”的分析方法,也称为“卡方检验”。
若总体的克莱姆相关系数的值为0,则“皮尔森卡方统计量
![]()

”为遵守卡方分布。
4. 虚无假说和对立假说:
虚无假说:就是“是”“XX为相等”的肯定假说;难以证明的假说;
对立假说:为“不是XX”“XX不相等”的否定假说;虚无假设对立的假说;

5. P值和”检验“的顺序:
(1)检验统计量是否在拒绝域中;
(2)P值是否小于置信水平;
(1)P值:独立性检验的P值即可,在虚无假说为真的情况下,则本次求出的值为大于或等于
![]()

值的机率。如:

(2)使用P值检验,顺序与上面的有些不同:
步骤6P:检验统计量值对应的P值,是否比置信水平小;
步骤7P:所得的P值若小于置信水平,即可作出"对立假说正确"的结论,反之则结论为"无法判定虚无假说为误"。
即使P值小于置信水平,以"检验"并无法作出"对立假说绝对正确"的结论。只能作出"虽然想说对立假说绝对正确,但是只能作虚无假说存在正确的机率为(P值*100%)"的结论。
6. 独立性检验和齐性检验:步骤顺序相同;
区别:3点;

6. 检验的结论表现:

附录:EXCEL计算各值的方法详见书中附录方法。

 )、调和平均数(
)、调和平均数(  );
);
 ; 样本标准差=
; 样本标准差=



![]() (每一数据-平均数)/标准差
(每一数据-平均数)/标准差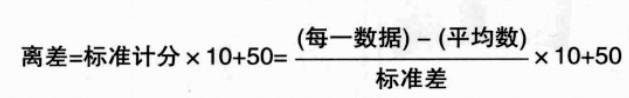



















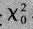 可以根据公式算出,具体方法自查。
可以根据公式算出,具体方法自查。













