RBF、GRNN、PNN神经网络学习笔记
RBF神经网络：径向基函数神经网络（Radical Basis Function）
GRNN神经网络：广义回归神经网络（General Regression Neural Network）
PNN神经网络:概率神经网络（Probabilistic Neural Network）
径向基函数神经网络的优点：逼近能力，分类能力和学习速度等方面都优于BP神经网络，结构简单、训练简洁、学习收敛速度快、能够逼近任意非线性函数，克服局部极小值问题。原因在于其参数初始化具有一定的方法，并非随机初始化（见习下面的代码）。
首先我们来看RBF神经网络
https://blog.csdn.net/ecnu18918079120/article/details/53365341/
隐藏层中神经元的变换函数即径向基函数是对中心点径向对称且衰减的非负线性函数，该函数是局部响应函数，具体的局部响应体现在其可见层到隐藏层的变换，跟其它的网络不同。
RBF神经网络的基本思想：用RBF（径向基函数）作为隐单元的“基”构成隐藏层空间，隐藏层对输入矢量进行变换，将低维的模式输入数据变换到高维空间内，使得在低维空间内的线性不可分问题在高维空间内线性可分。详细一点就是用RBF的隐单元的“基”构成隐藏层空间，这样就可以将输入矢量直接(不通过权连接)映射到隐空间。当RBF的中心点确定以后，这种映射关系也就确定 了。而隐含层空间到输出空间的映射是线性的(注意这个地方区分一下线性映射和非线性映射的关系)，即网络输出是因单元输出的线性加权和，此处的权即为网络可调参数。
《模式识别与只能计算》中介绍：径向基网络传递函数是以输入向量与阈值向量之间的距离|| X-Cj ||作为自变量的，其中|| X -Cj ||是通过输入向量和加权矩阵C的行向量的乘积得到。此处的C就是隐藏层各神经元的中心参数，大小为(隐层神经元数目*可见层单元数)。再者，每一个隐神经元中心参数C都对应一个宽度向量D，使得不同的输入信息能被不同的隐层神经元最大程度地反映出来。
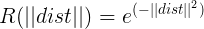
得到的这个R就是隐藏层神经元的值。
下图为径向基神经元模型
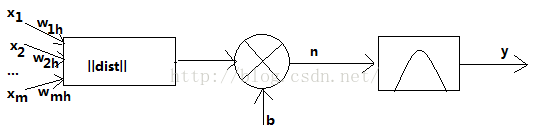
图中的b为阈值，用于调整神经元的灵敏度。RBF神经网络学习算法需要三个参数：基函数的中心，方差（宽度）以及隐含层到输出层的权值。
径向基函数神经网络（RBF）
线性层（加权和）
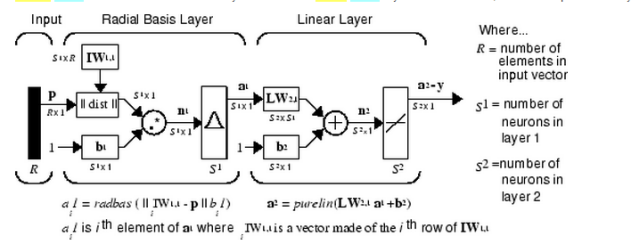
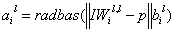IW1,1（输入层和隐藏层的权值）：输入训练矩阵转置
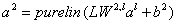LW2,1（输出层和隐藏层的权值）：求解特定的方程
代码里如何查看权值W1和阈值b1
W1 = net.iw{1,1};
b1 = net.b{1};
S1表示第一层的神经元个数，S2表示第二层的神经元个数；
输入层：p为列向量（R*1），即具有R个特征的输入向量；
第一层（径向基函数层）的权值矩阵大小为（S1*R），阈值b1（S1*1）；
第二层（线性层）的权值矩阵大小为（S2*S1），b2为（S2*1）。
利用径向基神经元和线性神经元可以建立广义回归神经网络，此种神经网络适用于函数逼近方面的应用。径向基函数和竞争神经元可以建立概率神经网络，此种神经网络适用于解决分类问题。
广义回归神经网络（GRNN）
特殊线性层
LW2,1（输出层和隐藏层的权值）也是一个确定的结果，由训练集的输出矩阵代替
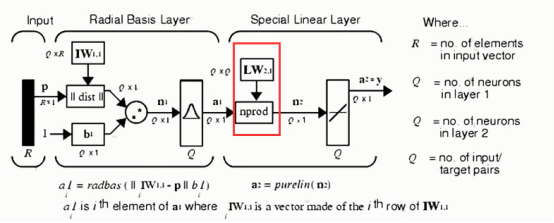
概率神经网络（PNN）
将线性层变成竞争层，在输出层用的不是线性函数，而是竞争函数competitive（只取出一个最大的训练集样本对应的label作为测试集预测的结果，重要函数（ind2vec））
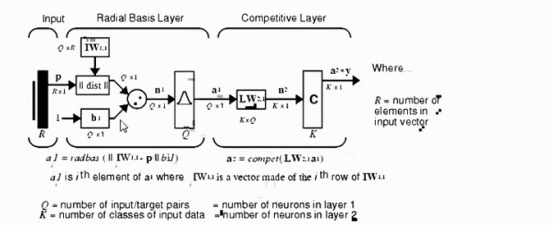
newrbe的参数初始化函数段：
function [w1,b1,w2,b2] = designrbe(p,t,spread)
[r,q] = size(p);
[s2,q] = size(t);
w1 = p'; %权值w1是输入训练矩阵的转置
b1 = ones(q,1)*sqrt(-log(.5))/spread; %阈值b1是一个固定的函数，和spread有关
a1 = radbas(dist(w1,p).*(b1*ones(1,q))); %隐藏层和输入层的的阈值和权值确定后，激活函数的a1也就能计算出来了
x = t/[a1; ones(1,q)];%输出层和隐含层的权值和阈值通过求解方程组的方式求解
w2 = x(:,1:q); %求解完了后就可以确定权值和阈值。
b2 = x(:,q+1);
重要的函数：
newrbe函数——创建一个精确型的径向基函数神经网络，调用格式
net = newrbe(P, T, spread)
newgrnn函数——创建一个广义回归神经网络
net = newrbe(P, T, spread)
newpnn函数——创建一个概率神经网络
net = newpnn(P, T, spread)
cputime——Elapsed CPU time 计算CPU消耗的时间
round（ceil、fix、 floor）——取整函数
Y = round（x）
length（size）——计算向量的长度矩阵的维度
n = length(x)
find——矩阵中某个元素的位置
[row, col] = find（X, ...）
Multiplication(.*) right division(./) left division(.\) power(.^)
matrix multiplication(*) matrix right division(/) matrix left division(\) matrix power(^)
RBF网络是一个三层的网络，除了输入输出层之外仅有一个隐层。隐层中的转换函数是局部响应的高斯函数，而其他前向型网络，转换函数一般都是全局响应函数。由于这样的不同，要实现同样的功能，RBF需要更多的神经元，这就是rbf网络不能取代标准前向型网络的原因。但是RBF的训练时间更短。它对函数的逼近是最优的，可以以任意精度逼近任意连续函数。隐层中的神经元越多，逼近越较精确.
径向基神经元和线性神经元可以建立广义回归神经网络，它是径RBF网络的一种变化形式，经常用于函数逼近。在某些方面比RBF网络更具优势。
径向基神经元和竞争神经元还可以组成概率神经网络。PNN也是RBF的一种变化形式，结构简单训练快捷，特别适合于模式分类问题的解决。
