5.线性回归算法

1.本节重点知识点用自己的话总结出来，可以配上图片，以及说明该知识点的重要性

 

线性回归的应用以及它的代码实现：

 

 

 

 

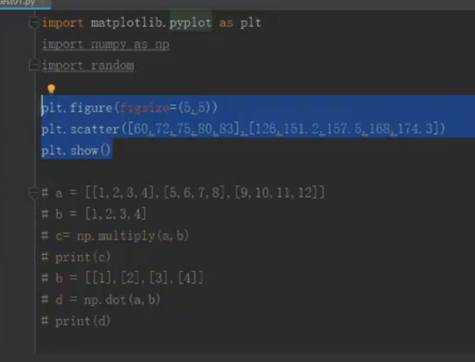
 线性回归的原理：

 

 

数组和矩阵的重要特性：

 

对于权重的求解：

 

 梯度下降算法原理：

 梯度下降的代码实现：

import random
import time
import matplotlib.pyplot as plt
_xs = [0.1*x for x in range(0, 10)]  # 自己造一些数据
_ys = [12*i+4 for i in _xs]
print(_xs)
print(_ys)
# 实现梯度下降
w = random.random()
b = random.random()

a1 = []
b1 = []
for i in range(100):
    for x, y in zip(_xs, _ys):
        o = w*x + b  # 预测值
        e = (o-y)  # 计算误差
        loss = e**2 # 计算损失
        # 求导
        dw = 2*e*x
        db = 2*e*1
        # 梯度下降
        w = w - 0.1*dw
        b = b - 0.1*db
        print('loss={0},w={1},b={2}'.format(loss, w, b))
    a1.append(i)
    b1.append(loss)
    plt.plot(a1, b1)
    plt.pause(0.1)

plt.show()

梯度下降的运行结果：

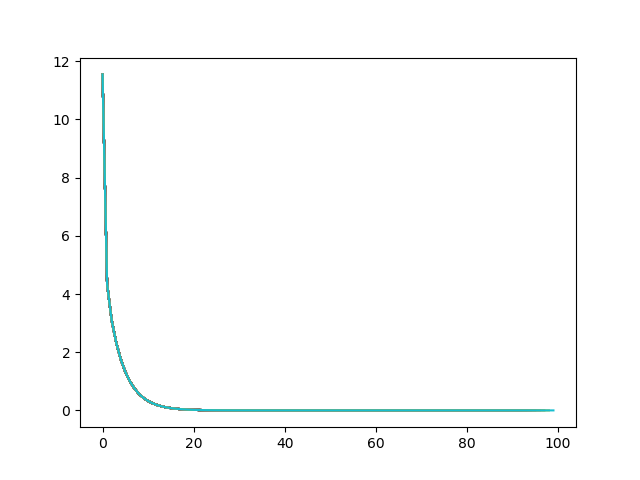
2.思考线性回归算法可以用来做什么？（大家尽量不要写重复）

　　线性回归可以用于：

　　（1）音乐流行趋势预测

　　（2）电影票房预估

　　（3）学生成绩排名预测

3.自主编写线性回归算法 ，数据可以自己造，或者从网上获取。（加分题）

 答：广告销量预测将来的投入和收益之间的关系。

Advertising数据集是关于广告收益与广告在不同的媒体上投放的相关数据，分别是在TV，Radio，Newspaper三种媒体上投放花费与，投放所产生的收益的数据。

 

（1）查看Advertising数据集：

 

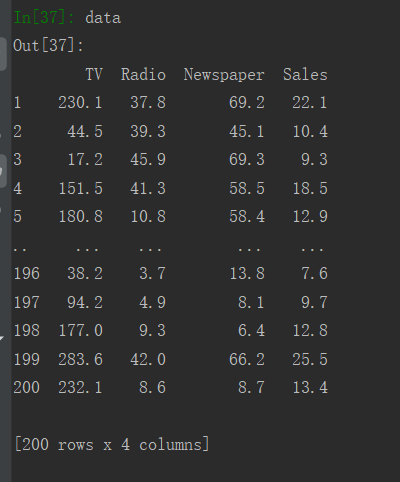
 （2）线性回归实现广告销量预测

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import matplotlib as mpl
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score

# 读取数据
data = pd.read_csv('advertising.csv', index_col=0)
#data1 = data[data['TV'].notna()]  # 把有空值的一行去掉
x = data1.iloc[:, :3]  # 自变量
y = data1.iloc[:, 3]  # 因变量

mpl.rcParams['font.sans-serif'] = ['simHei']
mpl.rcParams['axes.unicode_minus'] = False
# 划分训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=0)

model = LinearRegression()  # 构建模型
model.fit(x_train, y_train)  # 训练模型
# 查看模型参数
model.coef_    # 输出模型的权值
model.intercept_   # 截距
# 将自变量与对应系数进行打包
feature = ['TV', 'Radio', 'Newspaper']
a = zip(feature, model.coef_)
for i in a:
    print(i)
pre = model.predict(x_train)  # 预测
r2_score(y_train, pre)
# 模型预测
y_pre = model.predict(x_test)
r2_score(y_test, y_pre)
# 数据可视化
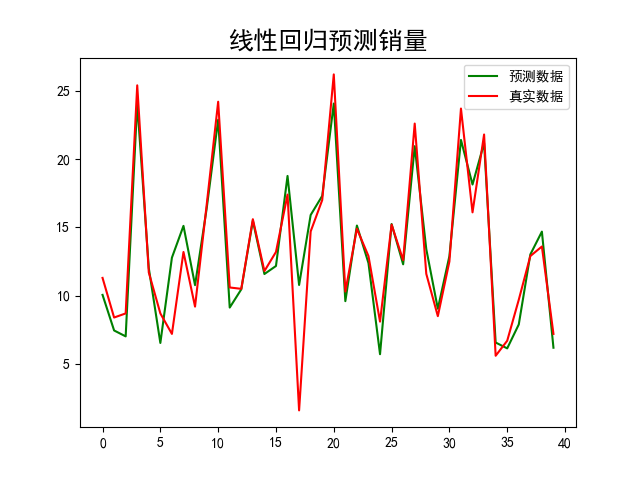
plt.plot(range(len(y_pre)), y_pre, color='green', label='预测数据')
plt.plot(range(len(y_pre)), y_test, color='red', label='真实数据')
plt.legend(loc='upper right')
plt.title('线性回归预测销量', fontsize=18)
plt.show()

 （3）绘制预测值与实际值曲线：