Java——归并排序

归并排序

• 归并排序是建立在归并操作上的一种有效的排序算法，该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

需求：

• 排序前：
• 排序后：

排序原理：

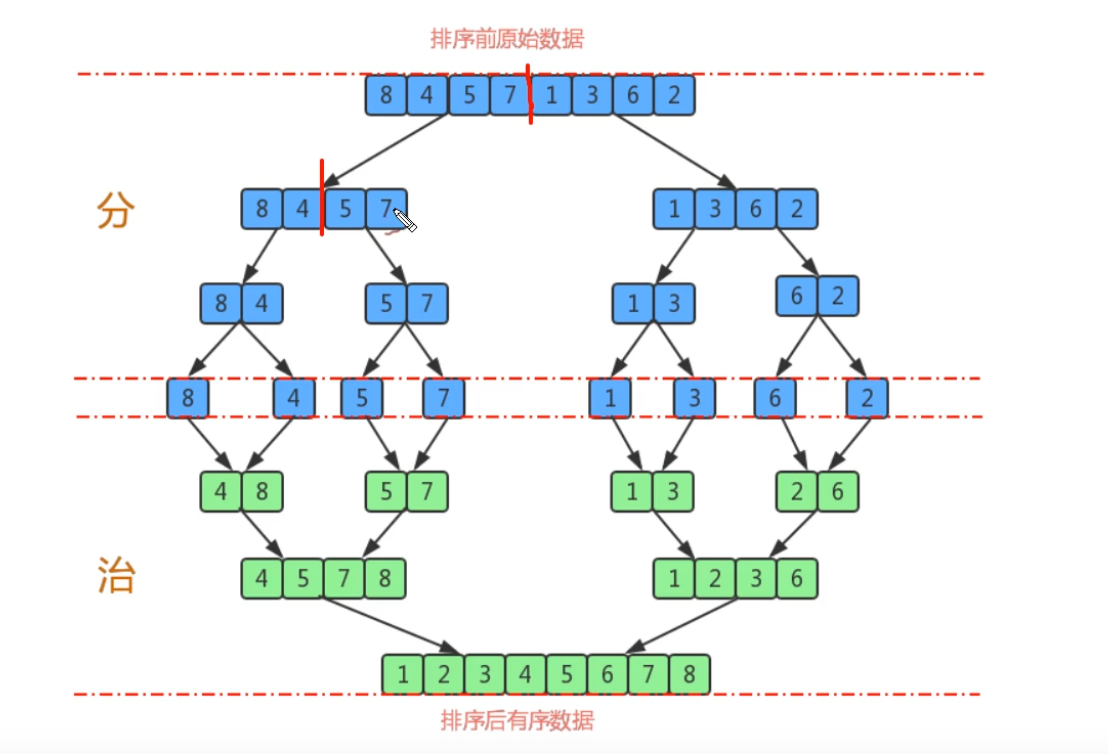
1.尽可能的一组数据拆分成两个元素相等的子组，并对每一个子组继续拆分，直到拆分后的每个子组的元素个数是1为止。

2.将相邻的两个子组进行合并成一个有序的大组；

3.不断的重复步骤2，直到最终只有一个组为止。

归并排序API设计：

类名	Merge
构造方法	Merge()：创建Merge对象
成员方法	1.public static void sort(Comparable[] a)：对数组内的元素进行排序
	2.private static void sort(Comparable[] a, int lo, int hi)：对数组a中从索引lo到索引hi之间的元素进行排序
	3.private static void merge(Comparable[] a, int lo, int mid, int hi):从索引lo到所以mid为一个子组，从索引mid+1到索引hi为另一个子组，把数组a中的这两个子组的数据合并成一个有序的大组（从索引lo到索引hi）
	4.private static boolean less(Comparable v,Comparable w):判断v是否小于w
	5.private static void exch(Comparable[] a,int i,int j)：交换a数组中，索引i和索引j处的值
成员变量	1.private static Comparable[] assist：完成归并操作需要的辅助数组

归并原理

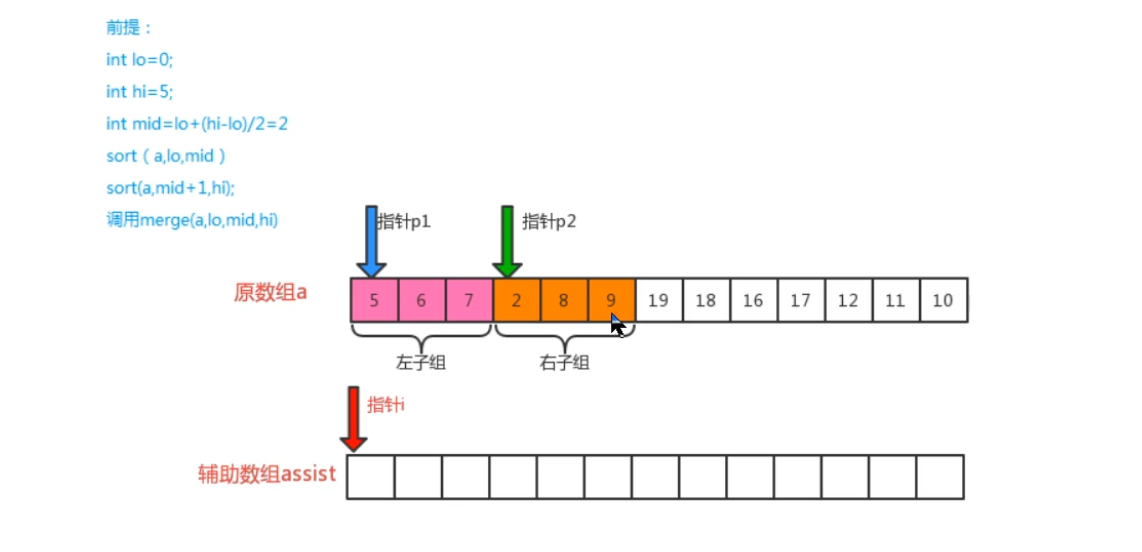
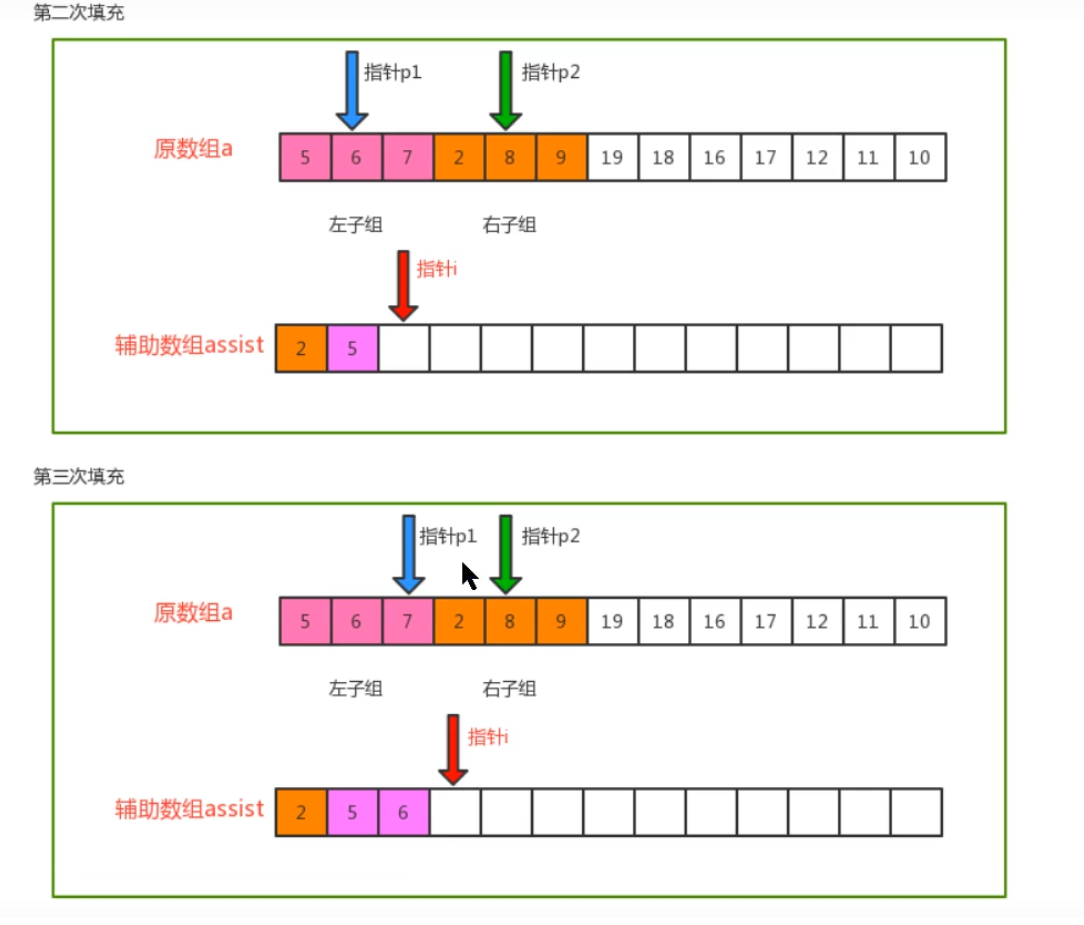
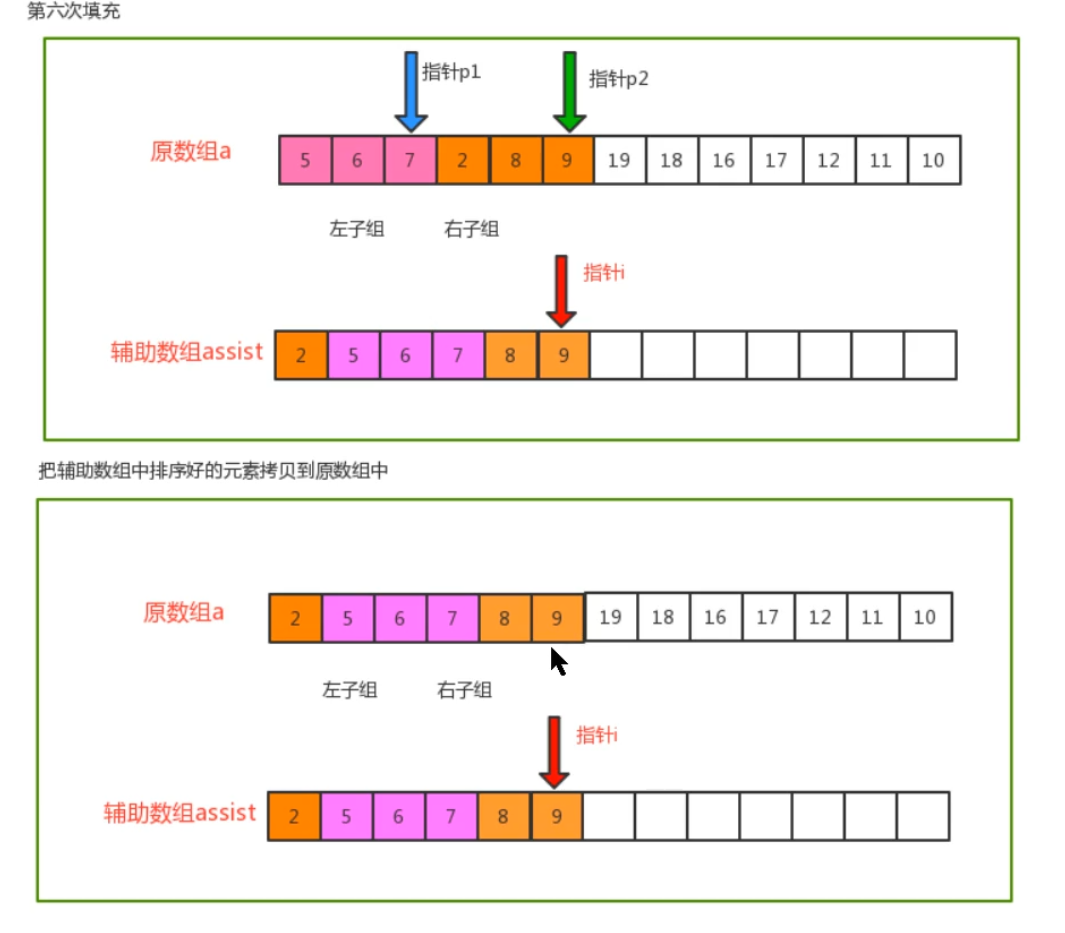
归并排序的代码实现：

// 归并排序
public class Merge {
    //归并所需要的辅助数组
    private static Comparable[] assist;

    /*
       比较v元素是否小于w元素
    */
    private static boolean less(Comparable v, Comparable w) {
        return v.compareTo(w) < 0;
    }

    /*
    数组元素i和j交换位置
     */
    private static void exch(Comparable[] a, int i, int j) {
        Comparable t = a[i];
        a[i] = a[j];
        a[j] = t;
    }


    /*
           对数组a中的元素进行排序
        */
    public static void sort(Comparable[] a) {
        //1.初始化辅助数组assist；
        assist = new Comparable[a.length];
        //2.定义一个lo变量，和hi变量，分别记录数组中最小的索引和最大的索引；
        int lo = 0;
        int hi = a.length - 1;
        //3.调用sort重载方法完成数组a中，从索引lo到索引hi的元素的排序
        sort(a, lo, hi);
    }

    /*
    对数组a中从lo到hi的元素进行排序
     */
    private static void sort(Comparable[] a, int lo, int hi) {
        //做安全性校验；
        if (hi <= lo) {
            return;
        }

        //对lo到hi之间的数据进行分为两个组
        int mid = lo + (hi - lo) / 2;//   5,9  mid=7

        //分别对每一组数据进行排序
        sort(a, lo, mid);
        sort(a, mid + 1, hi);

        //再把两个组中的数据进行归并
        merge(a, lo, mid, hi);
    }

    /*
    对数组中，从lo到mid为一组，从mid+1到hi为一组，对这两组数据进行归并
     */
    private static void merge(Comparable[] a, int lo, int mid, int hi) {
        //定义三个指针
        int i = lo;
        int p1 = lo;
        int p2 = mid + 1;

        //遍历，移动p1指针和p2指针，比较对应索引处的值，找出小的那个，放到辅助数组的对应索引处
        while (p1 <= mid && p2 <= hi) {
            //比较对应索引处的值
            if (less(a[p1], a[p2])) {
                assist[i++] = a[p1++];
            } else {
                assist[i++] = a[p2++];
            }
        }

        //遍历，如果p1的指针没有走完，那么顺序移动p1指针，把对应的元素放到辅助数组的对应索引处
        while (p1 <= mid) {
            assist[i++] = a[p1++];
        }
        //遍历，如果p2的指针没有走完，那么顺序移动p2指针，把对应的元素放到辅助数组的对应索引处
        while (p2 <= hi) {
            assist[i++] = a[p2++];
        }
        //把辅助数组中的元素拷贝到原数组中
        for (int index = lo; index <= hi; index++) {
            a[index] = assist[index];
        }

    }

}

// 测试代码
public class MergeTest {

    public static void main(String[] args) {
        Integer[] a = {8, 4, 5, 7, 1, 3, 6, 2};
        Merge.sort(a);
        System.out.println(Arrays.toString(a));//{1,2,3,4,5,6,7,8}
    }
}

归并排序的时间复杂度分析

• 归并排序是分治思想的最典型的例子，上面的算法中，对a[lo...hi]进行排序，先将它分为a[lo...mid]和a[mid+1...hi]两部分，分别通过递归调用将他们单独排序，最后将有序的子数组归并为最终的排序结果。该递归的出口在于如果一个数组不能再被分为两个子数组，那么就会执行merge进行归并，在归并的时候判断元素的大小进行排序。

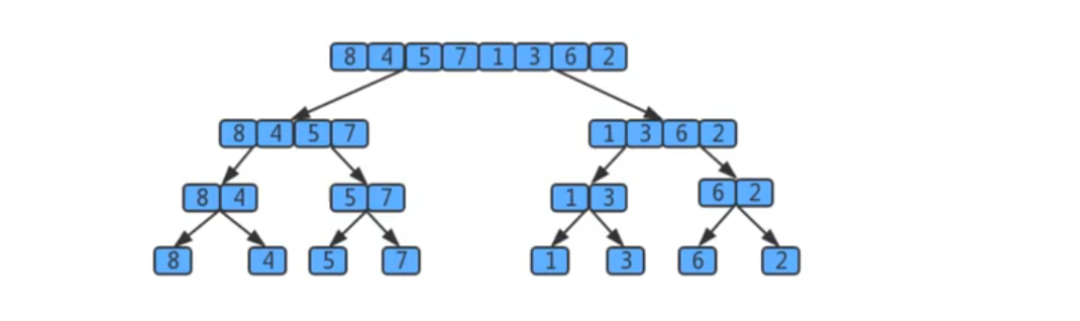
• 用树状图来描述归并，如果一个数组有8个元素，那么它将每次除以2找最小的子数组，共拆log8次，值为3，所以树共有3层,那么自顶向下第k层有2^{k个子数组，每个数组的长度为2}(3-k)，归并最多需要2^(3-k)次比较。因此每层的比较次数为 2^k * 2^(3-k)=23,那么3层总共为 3*2^3。
• 假设元素的个数为n，那么使用归并排序拆分的次数为log2(n),所以共log2(n)层，那么使用log2(n)替换上面32^3中 的3这个层数，最终得出的归并排序的时间复杂度为：log2(n) 2^(log2(n))=log2(n)*n,根据大O推导法则，忽略底数，最终归并排序的时间复杂度为O(nlogn);

归并排序的缺点

• 需要申请额外的数组空间，导致空间复杂度提升，是典型的以空间换时间的操作。

归并排序与希尔排序性能测试：

• 之前我们通过测试可以知道希尔排序的性能是由于插入排序的，那现在学习了归并排序后，归并排序的效率与希尔排序的效率哪个高呢？我们使用同样的测试方式来完成一样这两个排序算法之间的性能比较
• 在资料的测试数据文件夹下有一个reverse_arr.txt文件，里面存放的是从1000000到1的逆向数据，我们可以根据这个批量数据完成测试。测试的思想：在执行排序前前记录一个时间，在排序完成后记录一个时间，两个时间的时间差就是排序的耗时。

归并排序和希尔排序性能比较测试代码：

public class SortCompare {
    //调用不同的测试方法，完成测试
    public static void main(String[] args) throws Exception {
        //1.创建一个ArrayList集合，保存读取出来的整数
        ArrayList<Integer> list = new ArrayList<>();

        //2.创建缓存读取流BufferedReader，读取数据，并存储到ArrayList中；
        BufferedReader reader = new BufferedReader(new InputStreamReader(SortCompare.class.getClassLoader().getResourceAsStream("reverse_arr.txt")));
        String line = null;
        while ((line = reader.readLine()) != null) {
            //line是字符串，把line转换成Integer，存储到集合中
            int i = Integer.parseInt(line);
            list.add(i);
        }

        reader.close();


        //3.把ArrayList集合转换成数组
        Integer[] a = new Integer[list.size()];
        list.toArray(a);
        //4.调用测试代码完成测试
//        testInsertion(a);//34929毫秒
//        testShell(a);//43毫秒
        testMerge(a);//97毫秒
        

    }

    //测试希尔排序
    private static void testShell(Integer[] a) {
        //1.获取执行之前的时间
        long start = System.currentTimeMillis();
        //2.执行算法代码
        Shell.sort(a);
        //3.获取执行之后的时间
        long end = System.currentTimeMillis();
        //4.算出程序执行的时间并输出
        System.out.println("希尔排序执行的时间为：" + (end - start) + "毫秒");

    }

    //测试插入排序
    private static void testInsertion(Integer[] a) {
        //1.获取执行之前的时间
        long start = System.currentTimeMillis();
        //2.执行算法代码
        Insertion.sort(a);
        //3.获取执行之后的时间
        long end = System.currentTimeMillis();
        //4.算出程序执行的时间并输出
        System.out.println("插入排序执行的时间为：" + (end - start) + "毫秒");
    }

    //测试归并排序
    private static void testMerge(Integer[] a) {
        //1.获取执行之前的时间
        long start = System.currentTimeMillis();
        //2.执行算法代码
        Merge.sort(a);
        //3.获取执行之后的时间
        long end = System.currentTimeMillis();
        //4.算出程序执行的时间并输出
        System.out.println("归并排序执行的时间为：" + (end - start) + "毫秒");
    }
}

• 通过测试，发现希尔排序和归并排序在处理大批量数据时差别不是很大。