软件工程--个人项目作业

项目	内容
课程	软件工程
作业	个人项目作业
教学班级	005
GitHub地址	https://github.com/yankuai/Interset.git

PSP 表格

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划
· Estimate	· 估计这个任务需要多少时间	10	10
Development	开发
· Analysis	· 需求分析 (包括学习新技术)	60	120
· Design Spec	· 生成设计文档	40	40
· Design Review	· 设计复审 (和同事审核设计文档)	40	20
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	20	20
· Design	· 具体设计	60	180
· Coding	· 具体编码	180	180
· Code Review	· 代码复审	90	60
· Test	· 测试（自我测试，修改代码，提交修改）	120	180
Reporting	报告
· Test Report	· 测试报告	30	30
· Size Measurement	· 计算工作量	10	10
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	30	30
	合计	690	910

解题思路描述

总体思路

封装point，line和circle类。其中point类可以继承自STL pair<double,double>，line和circle类的属性应该体现其表达式的参数。

line一般式： \(ax+by+c=0\)

circle公式：\((x-x_0)^2+(y-y_0)^2=r^2\)

暴力算法寻找交点，计算每两个图形的交点，将交点放进STL set来去重，复杂度\(O(n^2)\)。

直线与直线的交点

直线的一般表示：

\(f(x) : ax + by + c = 0\)

已知直线上两点\((x_0,y_0),(x_1,y_1)\)，可以得到一般式的参数：

\(a = y_0 – y_1\)

\(b = x_1 – x_0\)

\(c = x_0*y_1 – x_1*y_0\)

以上两点坐标向直线一般式的转换在数据输入阶段完成。遍历直线计算交点时，由一般式计算直线交点的方程为：

\(x = (b_0*c_1 – b_1*c_0)/D\)

\(y = (a_1*c_0 – a_0*c_1)/D\)

\(D = a_0*b_1 – a_1*b_0\)

使用一般式的好处是，不需要单独考虑斜率为0的情况。

圆与圆的交点

回顾一下圆的两种表示方法：

圆的标准方程：\((x−x_0)^2+(y−y_0)^2=r^2\)

圆的参数方程：

\[\begin{equation} \begin{cases} x=x_0+r⋅cosθ\\ y=y_0+r⋅sinθ \end{cases} \end{equation}\]

将第一个圆的参数方程带入第二个圆的标准方程：
\((x_1+r_1 cosθ−x_2)^2+(y_1+r_1 sinθ−y-2)^2=r_2^2\)
展开后得到：
\(2 r_1(x_1−x_2)cosθ+2 r_1(y_1−y_2)sinθ=r_2^2−r_1^2−(x_1−x_2)^2−(y_1−y_2)^2\)

令：
\(a=2r_1(x_1−x_2)\)

\(b=2r_1(y_1−y_2)\)

\(c=r_2^2−r_1^2−(x_1−x_2)^2−(y_1−y_2)^2\)

原式变为：
\(acosθ+bsinθ=c\)

令\(cosθ=x,sinθ=\sqrt{1−x^2}\) ，关于sin**θsinθ 的正负后面再判断。
代入方程，得到，\(ax+b\sqrt{1−x^2}=c\)
移项再两边平方，\((ax−c)^2=b^2(1−x^2)\)
整理得，\((a^2+b^2)x^2−2acx+c^2−b^2=0\)，解一元二次方程得到\(x,sinθ,cosθ\)。

将\(sinθ\)和\(cosθ\)代回到第一个圆的参数方程，得到交点的坐标。

接下来需要注意，将求得交点带入第二个圆的方程验证，如果不在第二个圆上，说明\(sinθ\)是负数，需要对交点做调整。另一种特殊情况是，如果确定两个不同交点，解出来的\(cosθ\)只有一个，说明对应的\(sinθ\)值一正一负。

参考博客：https://www.cnblogs.com/AOQNRMGYXLMV/p/5098304.html

直线与圆的交点

求交点步骤如下

1. 首先求出圆心c在直线l 上的投影点pr的坐标

2. 计算向量p1p2的单位向量e, 再求出base的长度, 进而求出向量base

3. 最后,以pr作为起点, 向正or负方向加上该向量, 就可以得到圆与直线的交点了

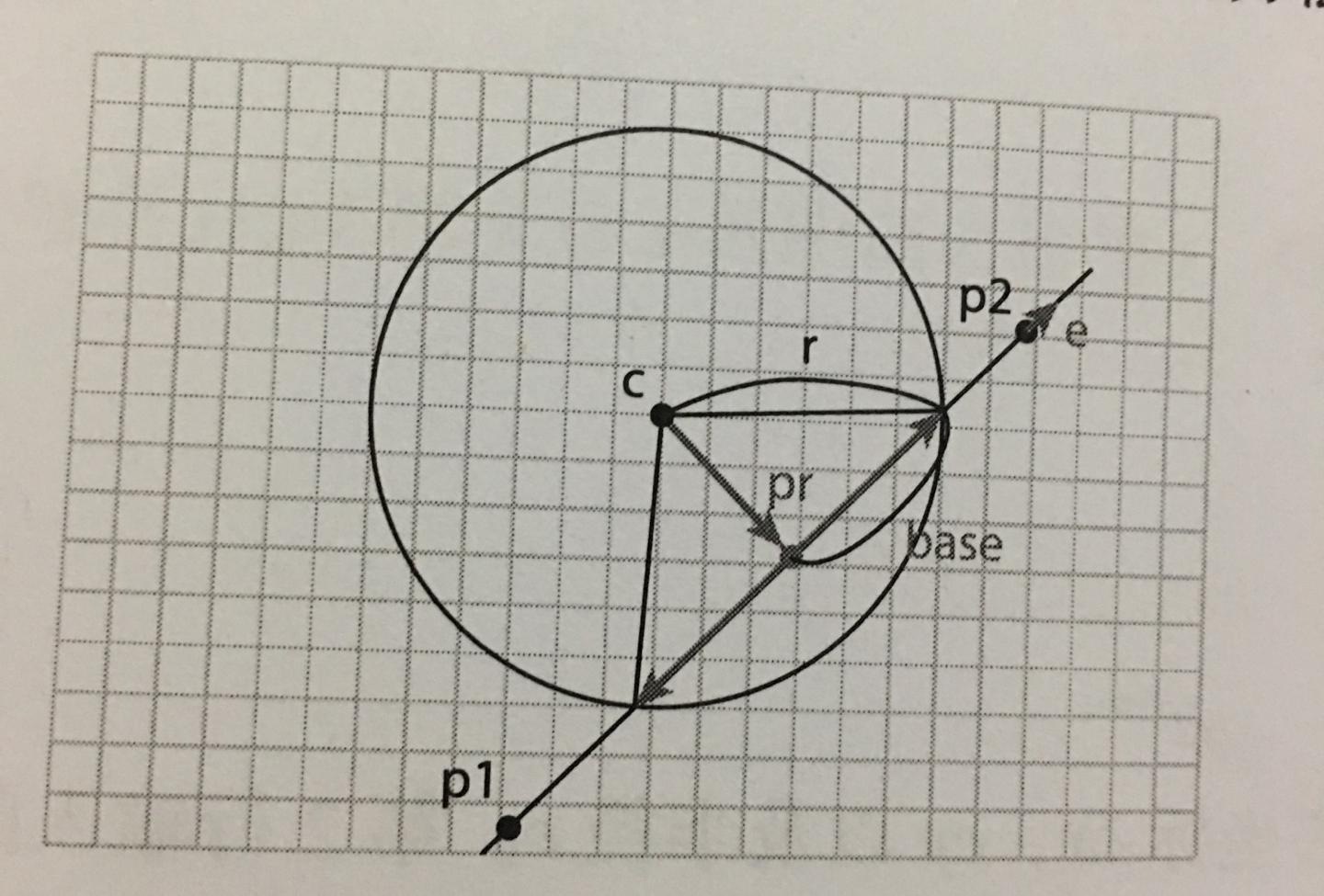
参考博客：http://www.pianshen.com/article/6764257/

设计实现过程

代码组织（几个类，几个函数，关系，关键函数流程图，单元测试设计）

代码组织

Point类

point不仅代表点坐标，还可以表示向量。在计算直线和圆的交点时，我运用了很多向量运算求圆心到直线的投影等，所以重写了operator方法，方便向量运算。

class Point : public pair<double, double> {
public:
	Point() {}
	Point(double x, double y);
	Point operator - (const Point& p);
	bool operator ==(const Point& p);
	void operator=(const Point& point);
	Point operator/(const double& d);
};

Line类

a,b,c是直线一般式的参数，e是直线的单位向量，p1,p2是确定直线的两点。

getIntersection_ll是求两直线交点的方法，传入set的指针，方法内直接将交点加入。

class Line {
public:
	double a;
	double b;
	double c;
	Point e;
	Point p1;
	Point p2;

	Line() {}
	Line(Point source, Point target);
	void operator=(const Line& line);
	int getIntersection_ll(set<Point>* intersections, Line l1, Line l2);
};

Circle类

getIntersection_cc是求两圆交点的方法。

class Circle {
public:
	Point c;
	double r;

	Circle() {}
	Circle(Point c, double r) :c(c), r(r) {}
	void operator=(const Circle& circle);
	int getIntersection_cc(set<Point>* intersections, Circle c1, Circle c2);
};

getIntersection_cl函数

求直线与圆交点的方法，不在line和circle类之中。其实把求两直线和两圆交点的方法分别放进line和circle类有些多此一举，因为参数还是会传入两个被观察的几何体，这两个方法类似于类中的静态方法，不用创建实例也可以用。

Geometry结构体

包含图形的标签（圆，直线），和图形自身的类。是为了实现将line和circle类存入一个vector容器，这样在遍历图形的时候更方便。

enum GType { L, C };

struct Geometry {
	GType Gflag;
	union {
		Line lObj;
		Circle cObj;
	};
	Geometry(Line l) {
		Gflag = L;
		lObj = l;
	}
	Geometry(Circle c) {
		Gflag = C;
		cObj = c;
	}
	void getObj(Line& obj) {
		if (Gflag == L) {
			obj = lObj;
		}
	}
	void getObj(Circle& obj) {
		if (Gflag == C) {
			obj = cObj;
		}
	}
};

参考博客：https://zouzhongliang.com/index.php/2019/06/22/stlrongqizhongcunfangbutongleixingshixianfangfa/

单元测试设计

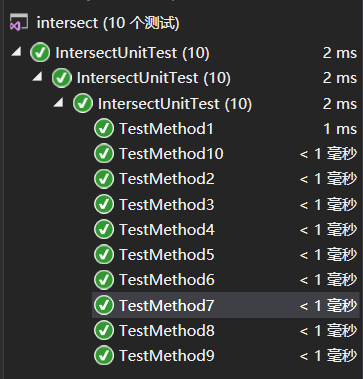
单元测试考虑了十种情况，包括直线与直线相交（相交、平行、斜率不存在），圆与圆相交（相离、内含、相切、相交），圆与直线相交（相离、相切、相交）。在这些情况下均能通过测试。

性能改进思路

性能分析图

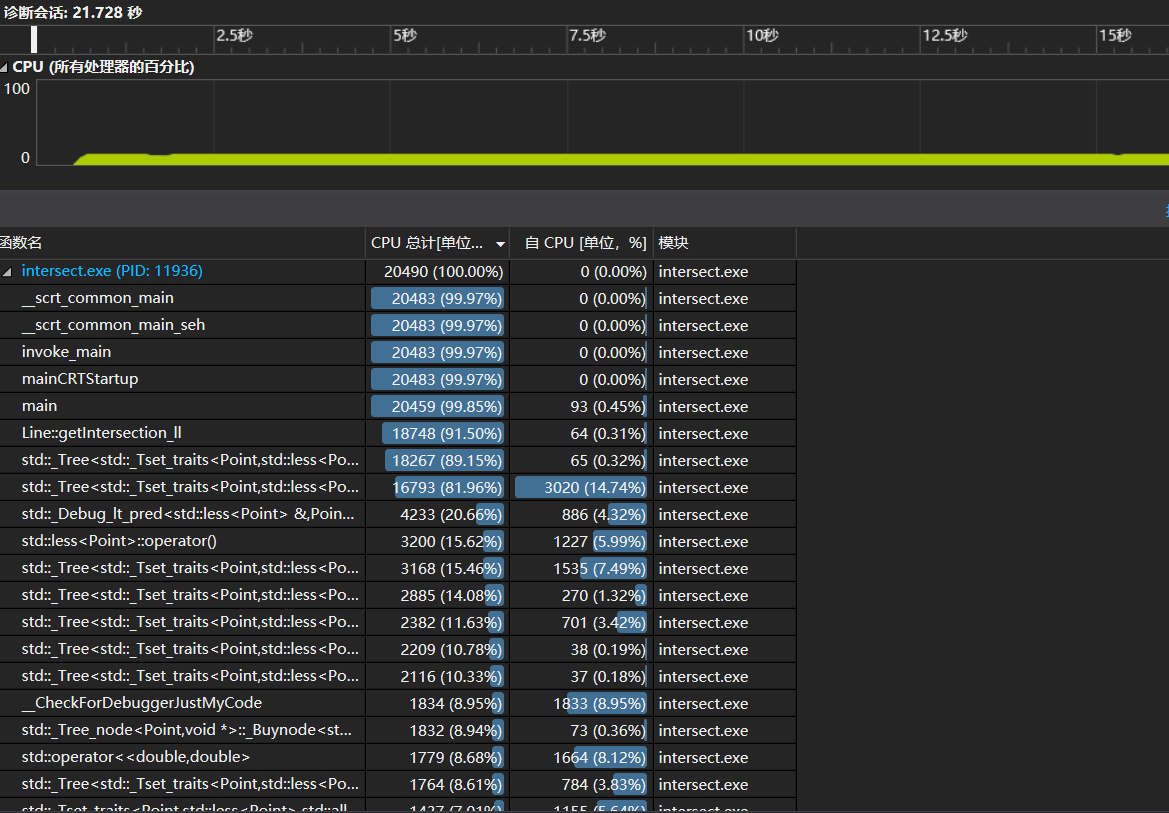
消耗最大的函数

将近90%时间都花在set的insert函数，其中两个点的比较运算最耗时。

改进思路

set的实现原理是红黑树，很难进一步优化。所以我尽量减少放进set的交点数，比如圆相切时，只把交点放进set一次。

代码说明

直线与直线交点

int Line::getIntersection_ll(set<Point>* intersections, Line l1, Line l2) {
	double D = l1.a * l2.b - l2.a * l1.b;
	if (D == 0) return 0;
	Point p = { (l1.b * l2.c - l2.b * l1.c) / D, (l2.a * l1.c - l1.a * l2.c) / D };
	p.first = (float)p.first;
	p.second = (float)p.second;
	intersections->insert(p);
	return 1;
}

圆与圆交点

int Circle::getIntersection_cc(set<Point>* intersections, Circle c1, Circle c2) {
	double r1 = c1.r, r2 = c2.r;
	double x1 = c1.c.first, x2 = c2.c.first, y1 = c1.c.second, y2 = c2.c.second;
	double d = length(c1.c - c2.c);		//dist of circle center

	if (dcmp(fabs(r1 - r2) - d) > 0) return -1;
	if (dcmp(r1 + r2 - d) < 0) return 0;

	double d2 = sqr(d);	//d*d
	double a = 2 * r1 * (x1 - x2);
	double b = 2 * r1 * (y1 - y2);
	double c = r2 * r2 - r1 * r1 - d * d;
	double p = a * a + b * b;
	double q = -2 * a * c;
	double r = c * c - b * b;

	double cosa, sina, cosb, sinb;
	//one intersection
	if (dcmp(d - (r1 + r2)) == 0 || dcmp(d - fabs(r1 - r2)) == 0) {
		cosa = -q / p / 2;													//被除数 p = a2 + b2 > 0
		sina = sqrt(1 - sqr(cosa));
		Point p(x1 + c1.r * cosa, y1 + c1.r * sina);
		if (!onCircle(p, c2)) p.second = y1 - c1.r * sina;
		p.first = (float)p.first;
		p.second = (float)p.second;
		intersections->insert(p);
		return 1;
	}
	//two intersections
	double delta = sqrt(q * q - 4 * p * r);
	cosa = (delta - q) / p / 2;
	cosb = (-delta - q) / p / 2;
	sina = sqrt(1 - sqr(cosa));
	sinb = sqrt(1 - sqr(cosb));
	Point p1(x1 + c1.r * cosa, y1 + c1.r * sina);
	Point p2(x1 + c1.r * cosb, y1 + c1.r * sinb);
	if (!onCircle(p1, c2)) p1.second = y1 - c1.r * sina;
	if (!onCircle(p2, c2)) p2.second = y1 - c1.r * sinb;
	if (p1 == p2) p1.second = y1 - c1.r * sina;
	p1.first = (float)p1.first;
	p1.second = (float)p1.second;
	p2.first = (float)p2.first;
	p2.second = (float)p2.second;
	intersections->insert(p1);
	intersections->insert(p2);
	return 2;
}

直线与圆交点

int getIntersection_cl(set<Point>* intersections, Circle c, Line l) {
	if (dcmp(disLine(c.c, l) - c.r) == 0) { return 0; }
	Point Base = vbase(c, l);
	Point pr = prxy(c, l);
	Point inter1 = { Base.first + pr.first, Base.second + pr.second };
	Point inter2 = { pr.first - Base.first, pr.second - Base.second };
	inter1.first = (float)inter1.first;
	inter1.second = (float)inter1.second;
	inter2.first = (float)inter2.first;
	inter2.second = (float)inter2.second;
	if (inter1 == inter2) {
		intersections->insert(inter1);
		return 1;
	}
	else {
		intersections->insert(inter1);
		intersections->insert(inter2);
		return 2;
	}
}

double disLine(Point p, Line l) {		//点到直线距离
	double a = l.a, b = l.b, c = l.c;
	double x = p.first, y = p.second;
	return fabs(a * x + b * y + c) / sqrt(a * a + b * b);	//a,b不同时为0
}

Point vbase(Circle c, Line l) {	//向量base
	double r = c.r;
	double base = sqrt(r * r - sqr(disLine(c.c, l)));
	return Point(l.e.first * base, l.e.second * base);
}

Point prxy(Circle c, Line l) {		//投影点pr的坐标
	Point A = l.p1;
	Point B = l.p2;
	Point O = c.c;
	Point AB = B - A;
	Point AO = O - A;
	double L = dot(AB, AO) / length(AB);
	Point Apr(l.e.first * L, l.e.second * L);
	return Point(A.first + Apr.first, A.second + Apr.second);
}

精度问题

可以发现，在进行交点比较的时候，使用了dcmp函数，而不是直接比较。dcmp允许比较数有些许误差，还是能返回相等的结果。造成大量的除法和开方运算造成了精度损失，使相同的交点坐标出现很小的差别。

int dcmp(double x) {
	if (fabs(x) < eps) return 0;
	return x < 0 ? -1 : 1;
}

另外在把交点加入set的时候，将double类型的坐标转换成float以降低精度，避免有细微差别的交点在集合里被当成两个不同的点。

我认为精度问题体现在两个地方，其一在计算交点坐标的时候，难免会有精度损失；其二在把交点放入集合的时候，比较交点时的比较精度会更高。是计算的低精度和比较的高精度造成的不适配，导致相同交点会在集合里出现两次。

• 方法一是提高计算精度，举例：

尽量把3.0计算成3.0000000000001而不是3.00001,这样在double省略掉后面位数时不会产生大误差。

• 方法二是降低比较精度，这里包括判断交点是否相等的显示比较(dcmp函数)，以及set内部去重的隐式比较。对于降低set内的比较精度，可以在数据加入set前用强制类型转换降低数据的精度，或者不改变数据而重写set比较函数。举例：

如果计算精度没有提升，已经把3.0算成3.00001，那比较时只看小数点后4位，3.00001就还是3.0。

这两个例子的精确度只为做示范，实际比较函数要估算到小数点后几位，是很值得研究的问题，我还没有找到答案（肯定不是例子的位数啦）。亲测在我选用不同精确度，计算上千条直线交点时，有不同的结果。

代码分析截图