【复习笔记】最优化方法 - 4. 约束优化方法

第四章 约束优化方法

本文是本人研究生课程《最优化方法》的复习笔记，主要是总结课件和相关博客的主要内容用作复习。

参考：

【1】https://blog.csdn.net/u012430664/article/details/78745729

【2】https://tfeima.github.io/2018/07/23/KKT%E6%9D%A1%E4%BB%B6--%E7%BA%A6%E6%9D%9F%E4%BC%98%E5%8C%96%E9%97%AE%E9%A2%98%E7%9A%84%E6%9C%80%E4%BC%98%E6%80%A7%E6%9D%A1%E4%BB%B6/

【3】https://www.jianshu.com/p/e36220b30d59

1. 约束优化问题的最优性条件

有效约束

非有效约束

有效集

关于最优性条件的概念比较混乱，整理如下：

课程PPT和课本中，都是上来直接就讲一般约束问题，而其他地方有的会分开讲。

• 等式约束问题的最优性条件
  • Lagrange定理（PPT里没说这部分）
• 不等式约束问题的最优性条件
  • 三个引理
    • Fakas引理
    • Gordan引理
    • （第三个引理没有名字，主要是关于下降方向集和可行方向集的交集，见上面博客【2】中“三个引理”部分）
  • 几何最优性条件（但是该条件难以直接应用）
  • Fritz-John一阶必要性条件
  • KKT一阶必要性条件（有的地方也称KT条件）
• 一般约束问题的最优性条件（这里的一般强调的是：既有等式约束，又有不等式约束的情况）
  • 几何最优性条件
  • Fritz-John一阶必要性条件（PPT中称为“代数最优性条件”）
  • KKT一阶必要性条件（有的地方也称KT条件）
  • 二阶最优性条件
    • 必要条件
    • 充分条件
  • 凸规划的最优性条件

需要掌握的内容是KKT条件和凸规划的最优性条件

1.1 KKT条件

设\(x^*\)是一般约束优化问题的局部最优解，若：

(i) \(f和c_i(i \in I)在x^*处可微；\)

(ii)\(c_i(i \in E)在x^*处一阶连续可微；\)

(iii)向量组\(\{ \nabla c_i(x^*)|i \in E\bigcup I(x^*) \}\)线性无关，

则存在不全为零的实数\(\lambda_i \ge0(i \in I \bigcup E)\)，使得

\(\begin{cases} \nabla f(x^*) - \sum_{i \in I \bigcup E} \lambda_i \nabla c_i(x^*) = 0,& \\ \lambda_ic_i(x^*)=0,& i\in I \\ \lambda_i \ge 0,& i\in I \end{cases}\)

1.2 凸规划的最优性条件

序列无约束方法（写在方法前面）

关于无约束问题，我们通过最优性条件能够直接求出解，那么这种方法称为解析法。

但是，对于有约束问题的一般情况是，我们很难通过最优性条件来得到最优解。通常情况下，使用KKT条件求解时，我们要求与约束个数同阶的矩阵的逆。我们可以容易验证某个点是否是最优解，但是很难直接求解。

由于无约束的最优化问题我们已经有了许多高效的解法，于是，对于有约束的问题，我们可以转化为求解无约束问题，并且用迭代算法来求解。这种方法称为序列无约束极小化技术SUMT（SequentialUnconstrained Minimization Technique）

算法类型总结：

• 外罚函数法 ---->适用于等式约束（也可用于不等式约束）
• 内罚函数法 ---->适用于不等式约束
• 乘子法
  • 等式约束下的乘子法：把所有等式约束加入到目标函数中即可
  • 不等式约束下的乘子法：先将不等式约束转变为等式约束，再利用等式约束下的乘子法

2. 序列无约束方法：外罚函数法

参考博客：

【1】https://blog.csdn.net/ice110956/article/details/17631765

2.1 简述

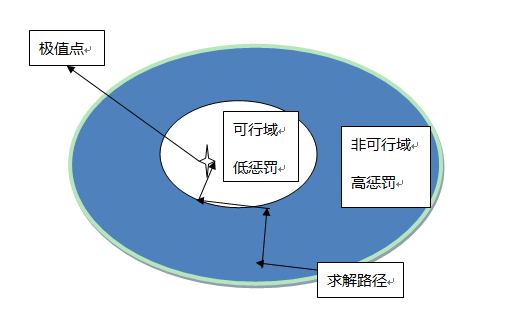
我们根据约束的特点，构造某种惩罚函数，然后加到目标函数中去，将约束问题求解转化为一系列的无约束问题。这种“惩罚策略”，对于无约束问题求解过程中的那些企图违反约束条件的目标点给予惩罚。如下图：

2.2 方法

对于等式约束：

对于不等式约束：

对于一般约束优化问题：

2.3 算法过程

2.4 优缺点与特征

缺点：

1. 近似最优解往往是不可解的。

2. 根据收敛性，\(\sigma\)越大越好；但是我们直接求解时，用到求导以及hesse矩阵，\(\sigma\)越大，越趋于病态，也就是不好解，这是乘子法所要解决的问题。

3. 序列无约束方法：内罚函数法

3.1 简述

参考博客：

【1】https://blog.csdn.net/ice110956/article/details/17631765

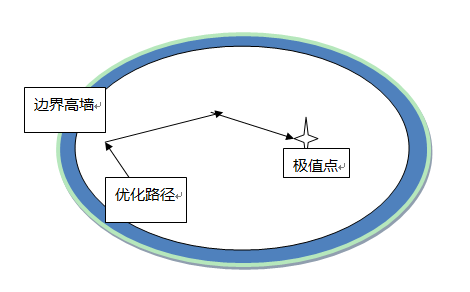
相比于外罚函数法在不可行区域加惩罚，内罚函数法在可行域边界筑起高墙，让目标函数无法穿过，就把目标函数挡在可行域内了。

这种惩罚策略只适用于不等式约束问题，并要求可行域的内点集非空，否则，每个可行点都是边界点，都加上无穷大惩罚，惩罚也就失去意义了。

3.2 方法

3.3 算法过程

3.4 优缺点与特征

4. 序列无约束方法：乘子法

4.1 简述

乘子法的存在是为了解决罚函数方法的主要缺陷：即当罚因子趋于无穷大或者趋近于0时，对应的罚函数的Hessen阵将变得越来越病态，似的无约束优化方法的计算难以进行下去。

4.2 乘子法解决等式约束问题

乘子的更新：

终止规则：

算法：

4.x 乘子法解决不等式约束问题

4.x 乘子法解决一般约束问题

算法

4.x 对于乘子法的理解部分：

摘自知乎一些大佬的回答