网页排序之PageRank
1、背景
在google创立初期,搜索网页排序使用的核心算法就是PageRank,成就其成为全球最大的搜索引擎。
2、PageRank
搜索引擎用户希望在查询过后,快速准确的找到用户需要的网页,因此需要行之有效的网页排名算法。谷歌的两位创始人的佩奇和布林,借鉴了学术界评判学术论文重要性的通用方法 — “论文的引用次数”。由此想到网页的重要性也可以根据这种方法来评价,于是PageRank就诞生了。
有别于词频和TF-IDF算法,PageRank的思路是将互联网看作一个有向图,其中把网页看作有向图的节点,文档间的超链接看作节点之间的边,并初始化一个权重。
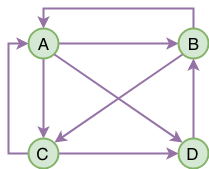
评估网页质量遵循两个假设:
- 数量假设:节点的入度越大,本页面的质量越高。(网页被链接数越多质量越高)
- 质量假说:节点的入度质量越高,本页面的质量越高。(被链接的网页质量与本网页质量正相关)
基于以上两个假设,假设有如下ABCD四个网页以及他们之间的链接关系。初始化阶段用户随机访问每个网页的概率是相等的,即初始化概率矩阵为 \(V_{0}\):
\[
\left[
\begin{array}{cccc}
\frac{1}{4} & \frac{1}{4} & \frac{1}{4} & \frac{1}{4}
\end{array}
\right]
\]
网页A分别指向BCD三个网页,因此A的状态转移概率为
\[
\left[
\begin{array}{cccc}
0 & \frac{1}{3} & \frac{1}{3} & \frac{1}{3}
\end{array}
\right]
\]
显然每一个网页都有指向其他网页的概率,把这些向量转置后合起来就是随机过程中的状态转移矩阵 \(T\) :
\[
\left[ \begin{array}{cccc} 0 & \frac{1}{2} & \frac{1}{2} & 0\\\\ \frac{1}{3} & 0 & 0 & 1\\\\ \frac{1}{3} & \frac{1}{2} & 0 & 0\\\\ \frac{1}{3} & 0 & \frac{1}{2} & 0 \end{array}\right]
\]
根据上述矩阵,我们计算经过一次网页跳转后用户访问的网页概率分布 \(V_{1} = T \cdot V_{0}\)
\[
V_{1} = T \cdot V_{0}=\left[ \begin{array}{cccc} 0 & \frac{1}{2} & \frac{1}{2} & 0\\\\ \frac{1}{3} & 0 & 0 & 1\\\\ \frac{1}{3} & \frac{1}{2} & 0 & 0\\\\ \frac{1}{3} & 0 & \frac{1}{2} & 0 \end{array}\right] \cdot\left[ \begin{array}{cccc} \frac{1}{4}\\\\ \frac{1}{4}\\\\ \frac{1}{4}\\\\ \frac{1}{4} \end{array}\right]=\left[ \begin{array}{cccc} \frac{6}{24}\\\\ \frac{8}{24}\\\\ \frac{5}{24}\\\\ \frac{5}{24} \end{array}\right]
\]
经过n次跳转后每个网页最终停留的概率为
\[
V_{n}=T \cdot V_{n-1}=T^n \cdot V_{0}
\]
佩奇和布林发现,当\(n\to +\infty\),且概率转移矩阵TT满足以 \(T\) 为随机变量、不可约且非周期时,\({\lim_{n\to+\infty}}V_{n}\) 最终收敛,保持在一个稳定值附近。以上节点迭代 \(10000\) 次后概率稳定在 \(\left[
\begin{array}{cccc}
0.265 & 0.294 & 0.235 & 0.205
\end{array}
\right]\) 附近,可见经过多次跳转后用户停留在B网页的概率最高。
3、总结
PageRank从节点\(V_{i}\)到节点\(V_{j}\)初始化节点权重\(S(V_{I})\)为1,链接在不断点击跳转中不断更新各个节点权重,每次按照如下更新:
\[
S(V_{i})=(1-d)+d \times \sum_{V_{j}\in In(V_{i})}\frac{1}{\left|Out(V_{j})\right|}S(V_{j})
\]
其中\(d\)为上述转移概率 \(d\in(0,1)\),\(In(V{i})\)是链接到\(V_{i}\)节点的链接集合,\(Out(V_{j})\)是从节点\(V_{j}\)出发到外链的节点集合。
- 因此可见并不是网站外链越多其PageRank就越高,网站给别的网站外链越多,每条外链的权重越低;
- 根据公式 \(\frac{1}{\left|Out(V_{j})\right|}S(V_{j})\) ,外链的权重和总链接数量成反比,与提供外链的网站权重成正比,例如说,给定一个节点的外链全是低权重外链,那么迭代过程中该节点权重不断降低,同时它给出去的链接权重也是不断降低,形成连锁反应。
虽然现在Google搜索用到了深度学习等方式的排序方式,但不得不说PageRank对Google意义重大,并且其变型TextRank在文本中也有重大应用,我们在下节讲解。

