【2020.02.18】反向传播、线性回归
本期的学习来源是:https://www.bilibili.com/video/BV1Y7411d7Ys?p=4
代码来源于:https://blog.csdn.net/bit452/article/details/109643481
反向传播
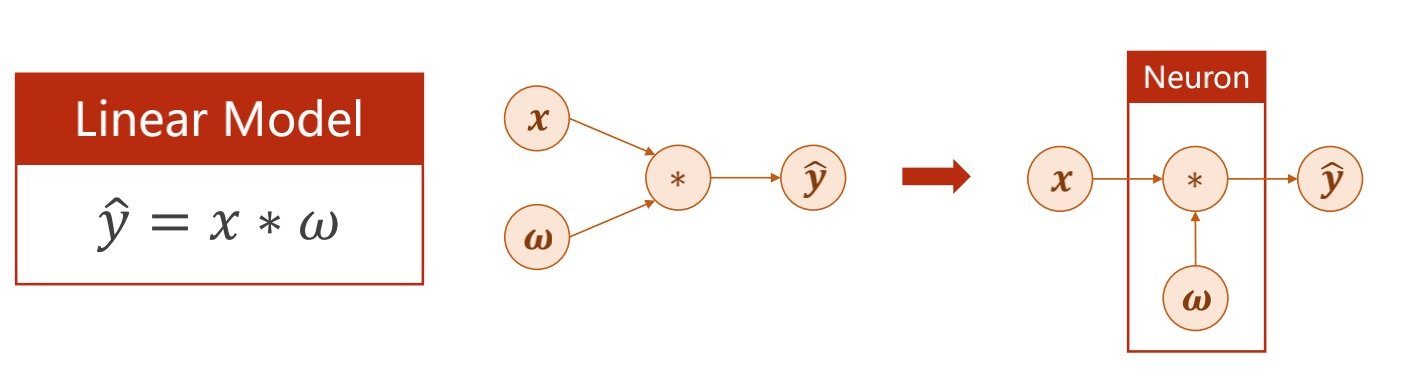
简单的线性模型中,X是输入,W是权重,权重是训练的目标,而Y_hat则是最终的输出
权重可不仅是数字,还可以是矩阵
更新权重的过程,不是计算Y_hat对其的倒数,而是损失对权重的倒数
(要使得损失最小而不是Y_hat最小
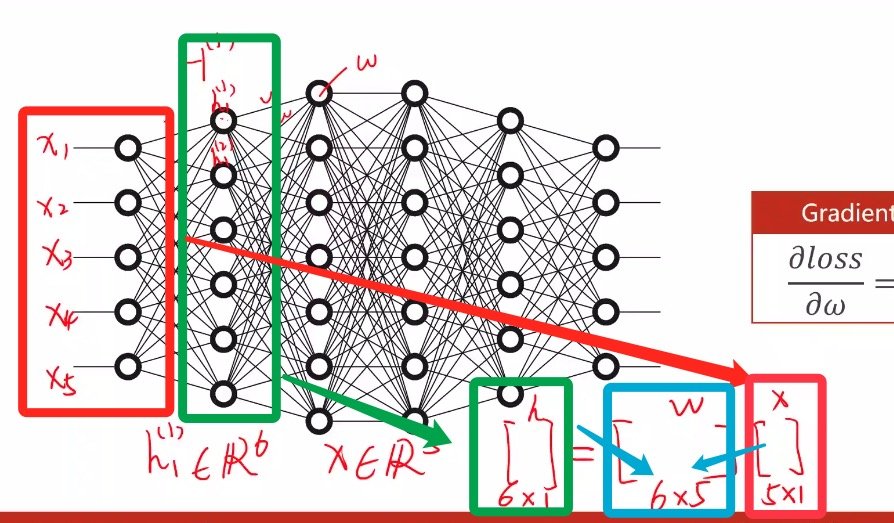
在下图的网络中,每一条连线都是一个权重
在初始的输入值只有五个的情况下(相当于5*1的矩阵输入),要转入第一层(有6个,相当于6*1的矩阵)
那么就可以推导出权重矩阵是6*5的矩阵,说明有30个权重
(例如第一层和第二层的话就是6*7=42个权重
权重过多所以无法写出解析式
因此我们要设计反向传播的算法,通过设计图,在图上传播梯度,根据链式法则求出梯度
激活函数
如下图中两层的情况
图上MM表示的是矩阵乘法,ADD是向量加法
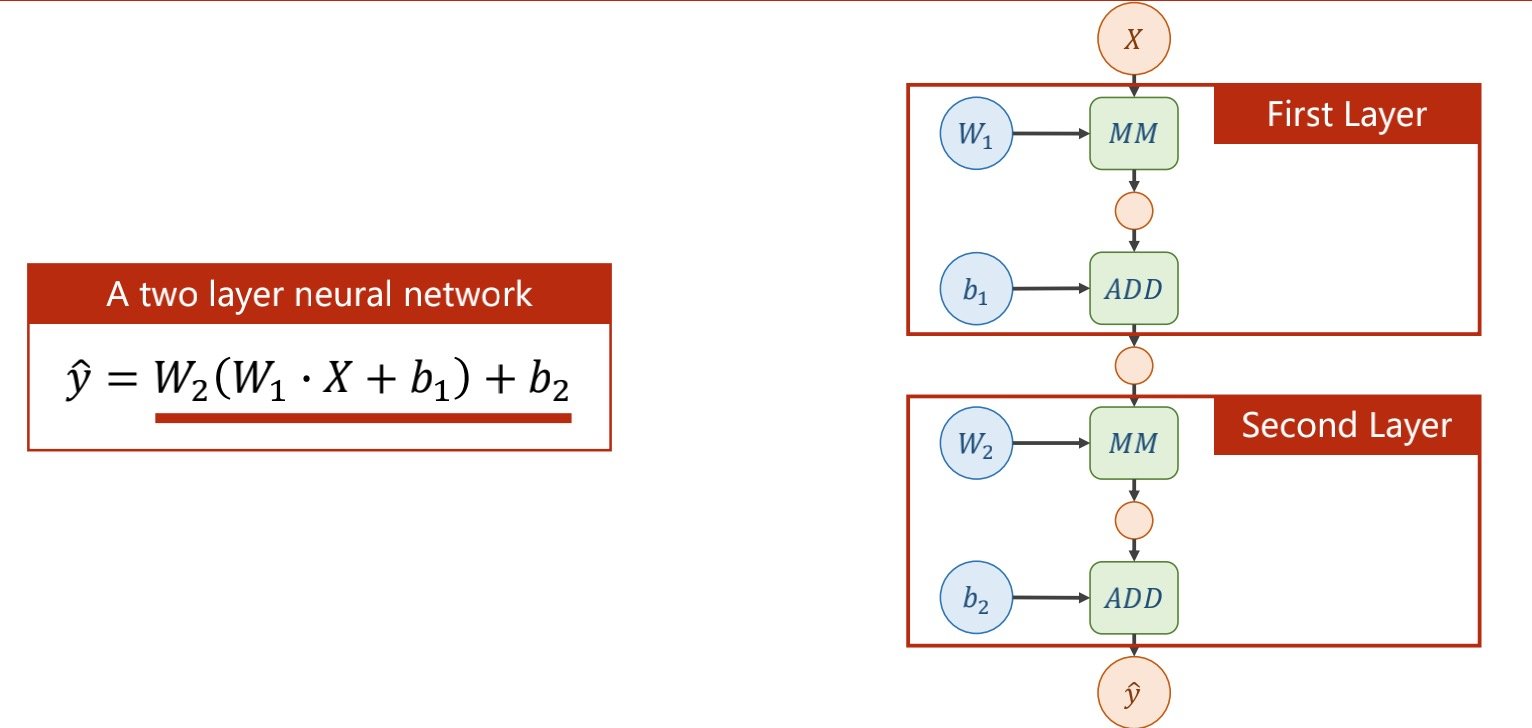
但为了防止两个权重矩阵直接化简,如下图所示
(否则上层的权重就毫无意义了,所有的深度最终只会变为一层
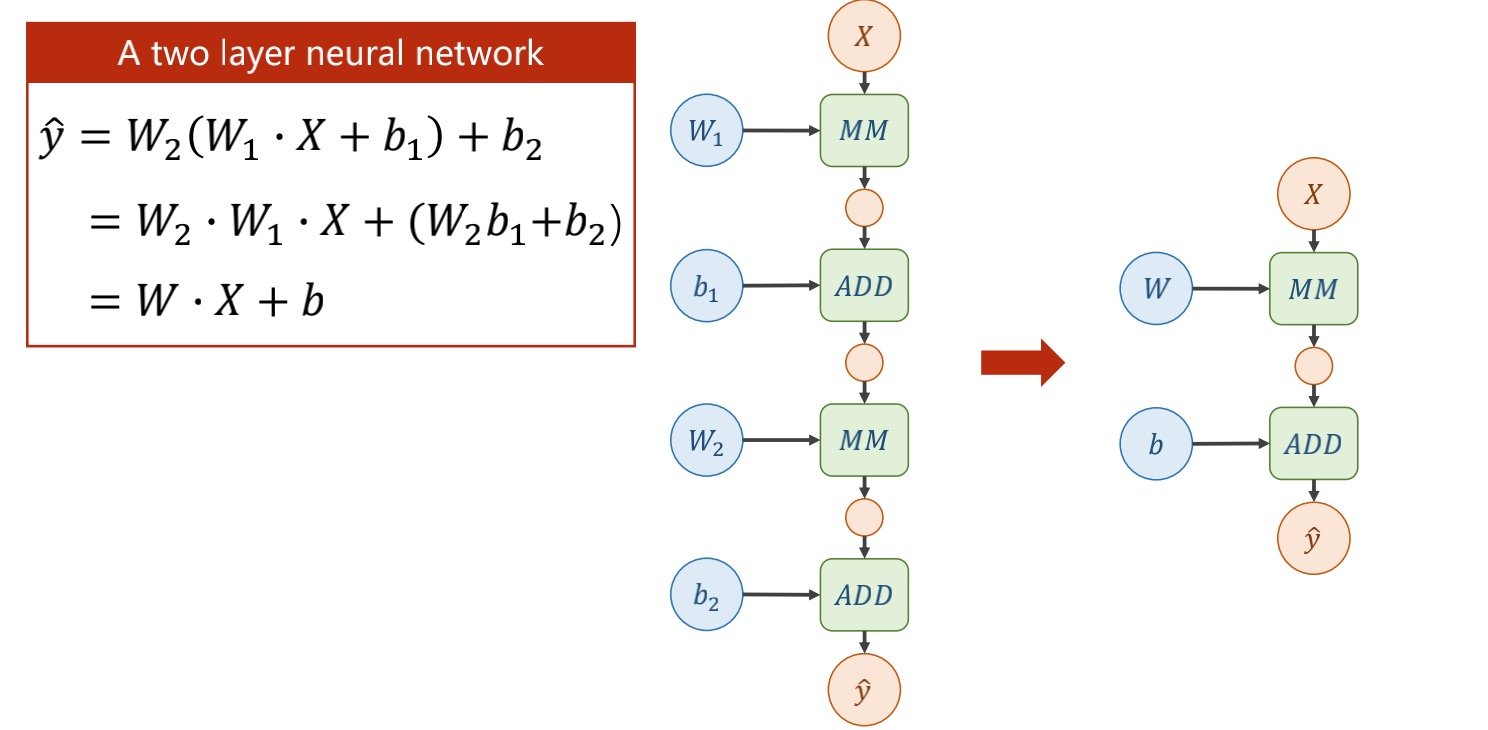
因此要在每一次的末尾进行非线性函数的变化
使得上一层的输出是下一层的输入
这个非线性函数的变化被称为激活函数
加了激活函数之后神经网络才有了能够逼近任意函数形式的能力
其中的过程可以形象比喻成下图
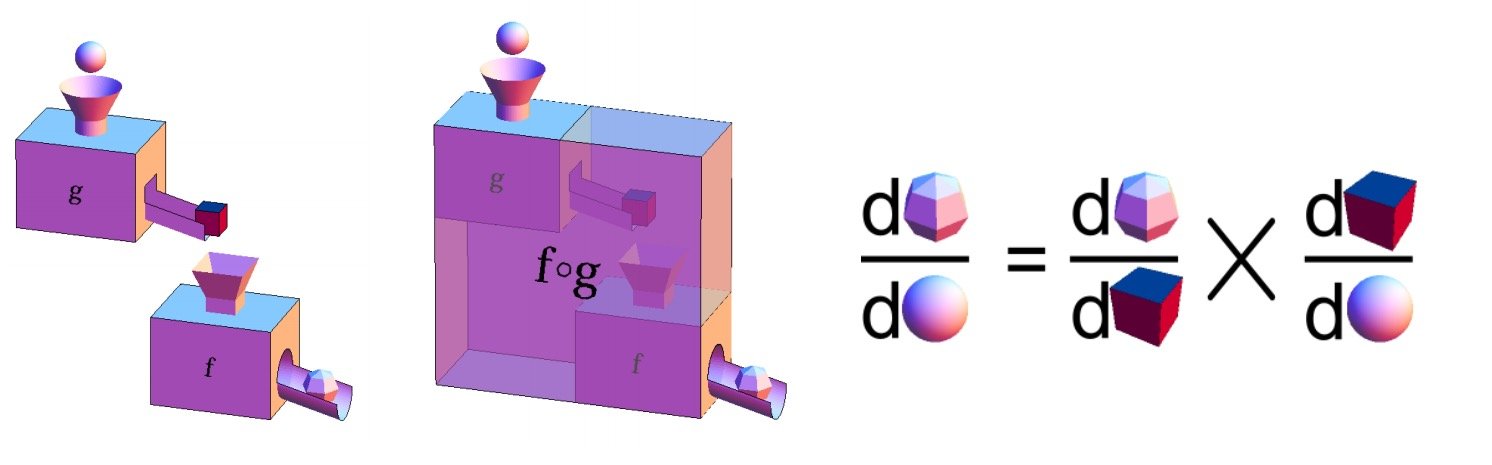
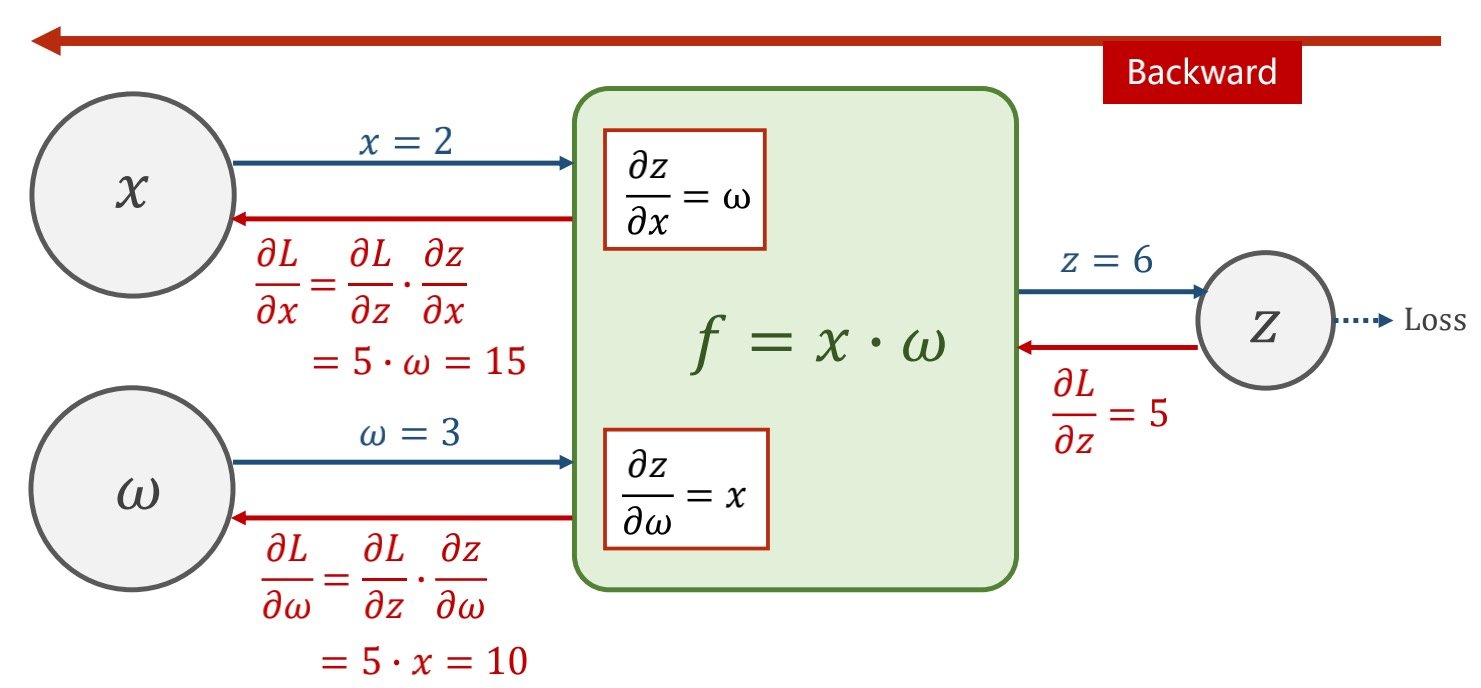
具体例子可以见下图
算出局部的梯度,当拿到损失函数时候,就可以通过梯度传播,算出前部的梯度
pytorch最后会将梯度存到变量里,而不是存到计算模块里
先走前馈的过程得到Loss
再走反向的过程求出梯度
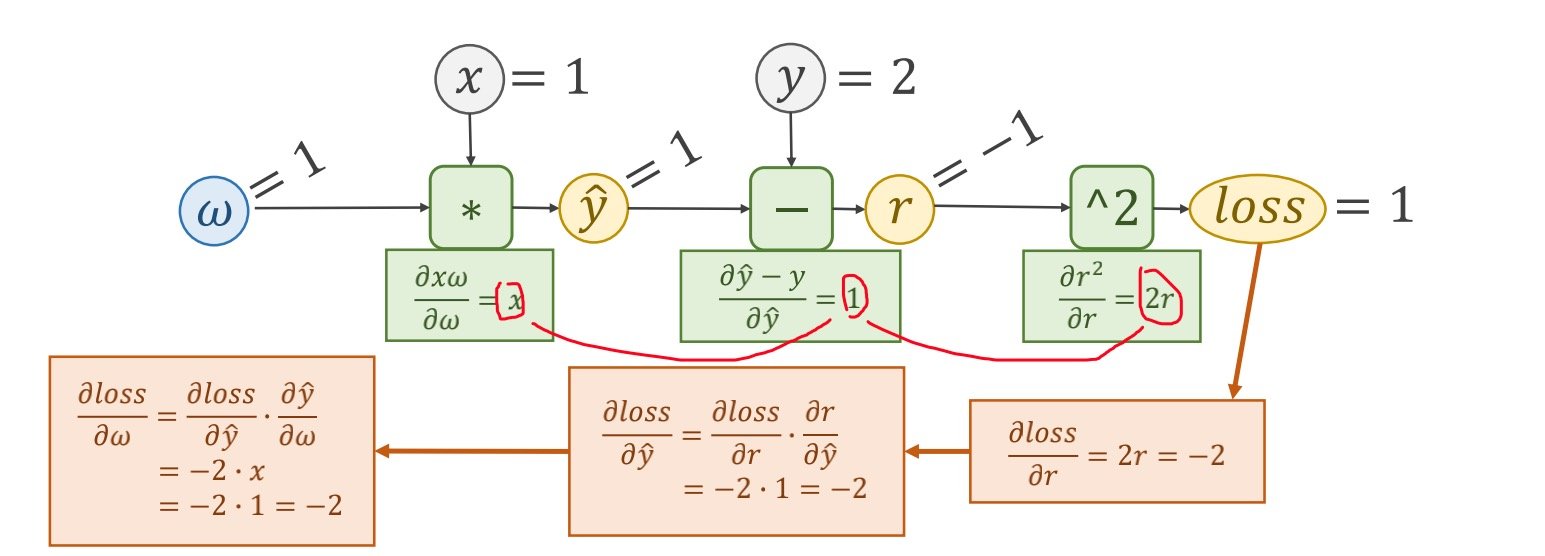
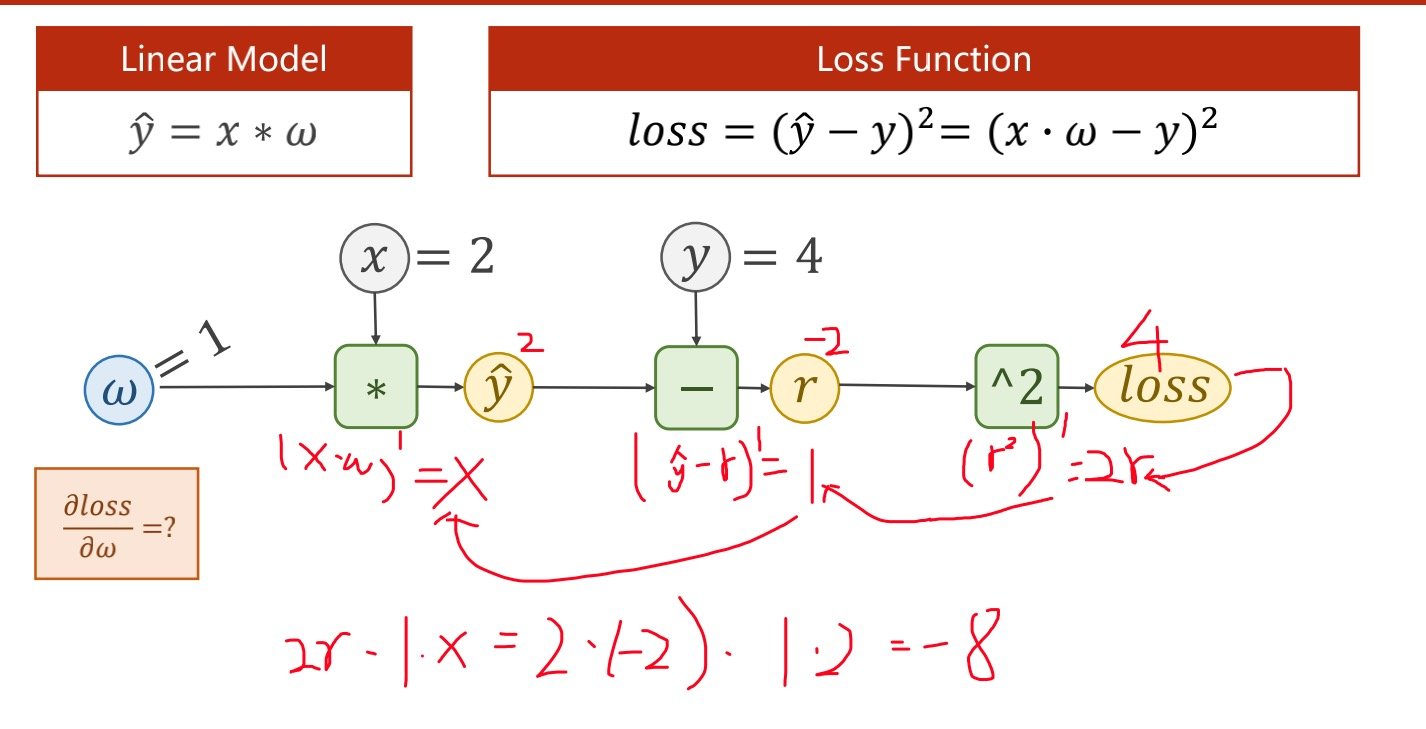
张量(tensor)
张量中保存着data和grad,其中data可以是标量向量矩阵等
grad指的是损失函数对权重的导数
不论是data还是grad,都是一种tensor,而梯度默认为none
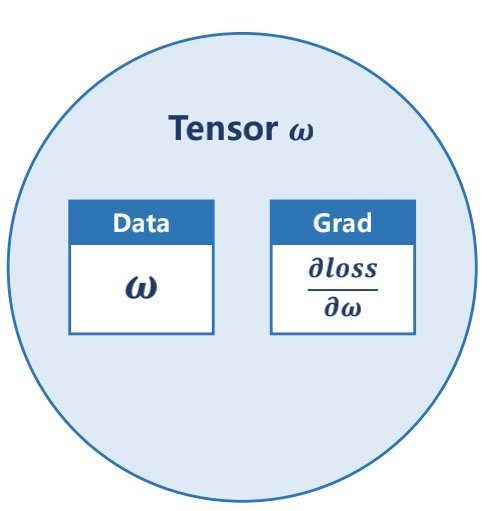
因此在创建tensor时候默认是不会计算梯度grad的,所以在创建tensor时候需要在后面加入
.requires_grad = True
函数调用l.backward()方法后w.grad为Tensor
故更新w.data时需使用w.grad.data。如果w需要计算梯度,那构建的计算图中,跟w相关的tensor都默认需要计算梯度

从下列代码中就可以比较明晰地看出
(注意type()那一行的代码
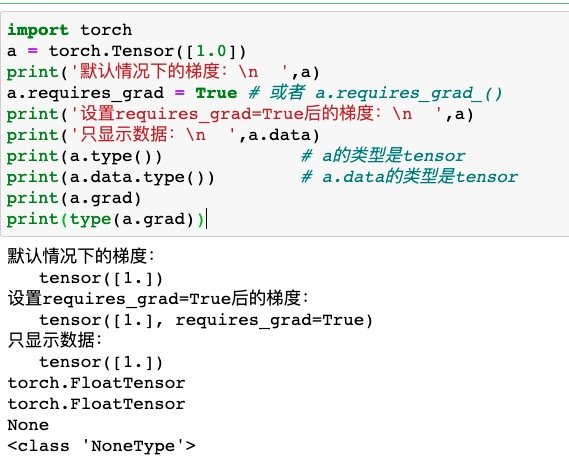
import torch
a = torch.Tensor([1.0])
print('默认情况下的梯度:\n ',a)
a.requires_grad = True # 或者 a.requires_grad_()
print('设置requires_grad=True后的梯度:\n ',a)
print('只显示数据:\n ',a.data)
print(a.type()) # a的类型是tensor
print(a.data.type()) # a.data的类型是tensor
print(a.grad)
print(type(a.grad))
使用反向传播的方法例子
在计算方面上使用.data,在输出时候对tensor对象使用.item()
import torch
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w = torch.Tensor([1.0]) # w的初值为1.0
w.requires_grad = True # 需要计算梯度
def forward(x):
return x*w # w是一个Tensor
def loss(x, y):
y_pred = forward(x)
return (y_pred - y)**2
# 通过上面的三个样本,此时需要预测input=4时,前向传播的结果
print("predict (before training)", 4, forward(4).item(), '\n')
for epoch in range(100):
for x, y in zip(x_data, y_data):
l =loss(x,y) # 前向传播算出损失,l是一个张量,tensor主要是在建立计算图 forward, compute the loss
# 使用.backward()函数的时候会自动反向传播算出梯度grad值,并记录在变量里
l.backward() # backward,compute grad for Tensor whose requires_grad set to True
print('\tgrad:', x, y, w.grad.item())
w.data = w.data - 0.01 * w.grad.data # 权重更新时,需要用到标量,注意grad也是一个tensor,因此这里要加上.data
w.grad.data.zero_() # after update, remember set the grad to zero
print('progress:', epoch, l.item(), '\n') # 输出轮数和损失函数
# 取出loss使用l.item,不要直接使用l(l是tensor会构建计算图)
print("predict (after training)", 4, forward(4).item())
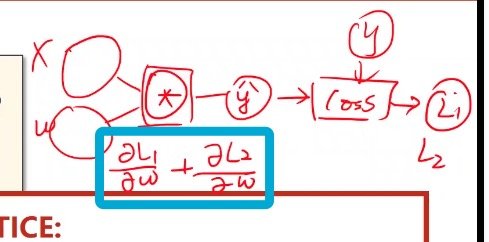
在更新完权重后,需要使用.grad.data.zero_(),清零本轮获得的梯度值
如果缺乏这一步,实现的效果将会是,加上上一轮损失函数对权重的导数,这就不是我们想要的结果了
线性回归
主要分为以下步骤
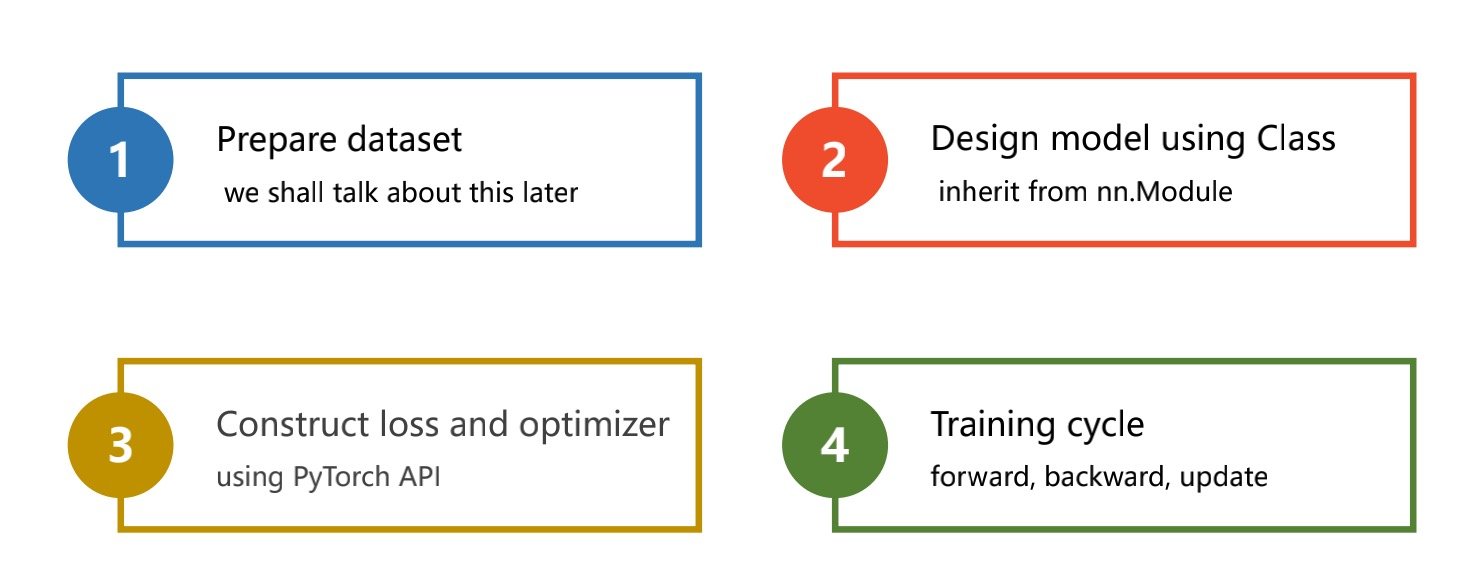
- 准备数据集
- 设计模型(线性等
- 算出损失函数,构建优化器(其中在构建损失函数和计算反向梯度的之间要将梯度清零
- 不断训练已达到更新权重值的目的
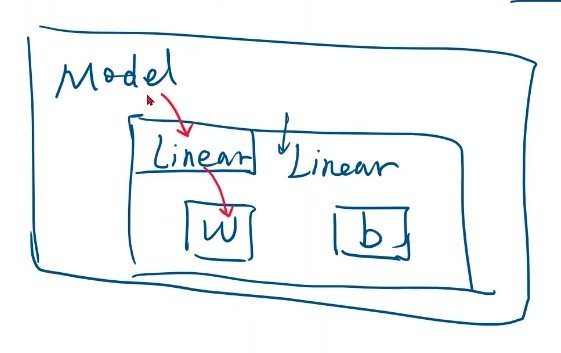
module建立
(构造神经网络,是用来计算Y_hat的,例如Y_hat=w*x+b这个式子就是一个模型)
列数是维度
需要同时知道输出值和输入值的维度,才能知道权重值的维度
但是最后要算出的loss值是标量(即使是tensor类型,也要求和/求平均值,求得平均值,
模型要定义成一个类,基础的模板如下(会自动构造backward的函数)
class LinearModel (torch.nn.Module):
def _init_(self):
super(LinearModel,self).__init__() # 父类的构造,这一步一定要有,just do it
self.linear=torch.nn.Linear(1,1) # torch.nn.Linear是pytorch的一个类,类的后面加括号,是在创建一个对象
# 这一步创建对象包含了权重W和偏置b
def forward(self,x):
y_pred=self.linear(x)
return y_pred
model = LinearModel() # 实例化直接调用
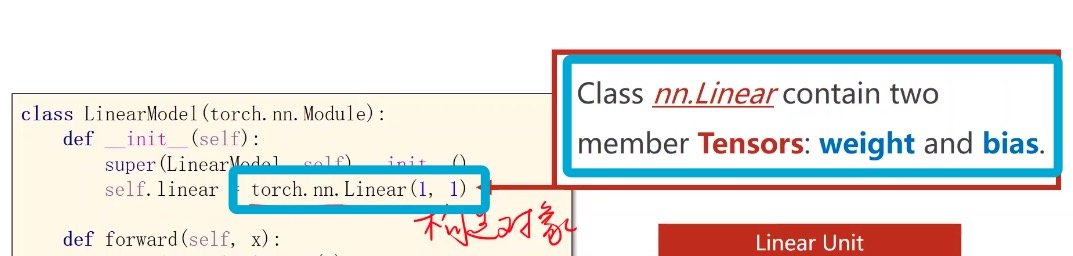
torch.nn.Linear()具体解析
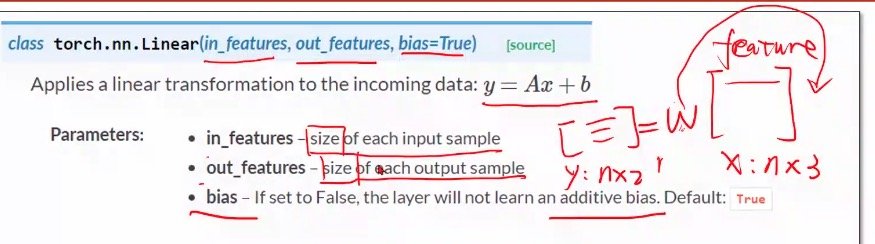
父类的解析:https://www.runoob.com/python/python-func-super.html
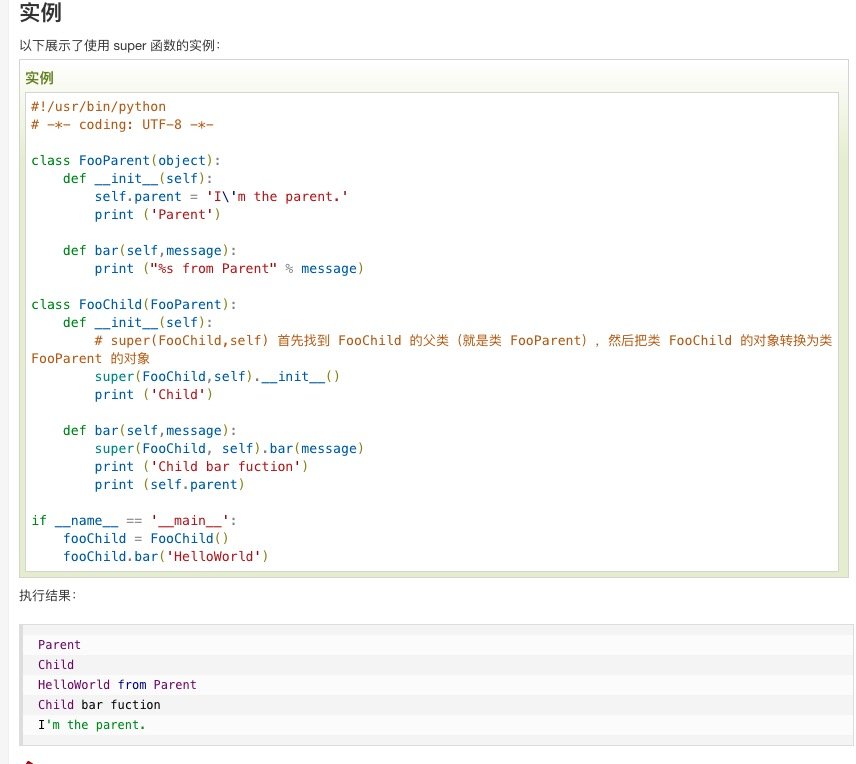
在通常情况下,y的表示方法为:行作为feature的数量,列作为样本数,在进行计算的时候再进行转置
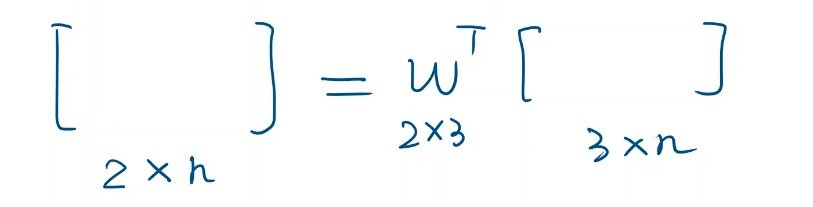
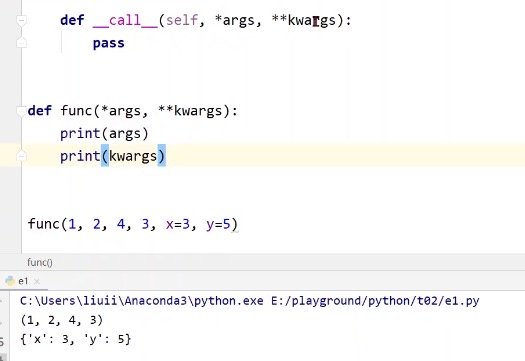
_call_()函数的使用
如果想要调用函数的话,就得在类中定义__call__(),在默认情况下会在括号内自动补全__call__(self, *args, **kwargs)
这个*args的意思是,当你未定义形参的时候,多传入的部分会被作为元组进行使用
这个**kwargs的意思是,带等于号的关键字形参,会被当作词典
具体的效果可以看下方
元组列表数组的区别:https://www.cnblogs.com/260554904html/p/8125641.html
构造损失函数、优化器
优化器(optimizer)不会构成计算图
在构建损失函数和计算反向梯度的之间要将梯度清零
loss.backward() # 反向传播,计算梯度
optimizer.step() # update 参数,即更新w和b的值
训练过程
在每一次的循环中要做的几件事
-
算出y_hat值
-
与实际y值算出损失函数(其中在构建损失函数和计算反向梯度的之间要将梯度清零
-
构建反向梯度
-
更新权重值


最后在打印权重值的时候

之所以这样子打印,是为了调用
linear是module里面的类,然后经过实例化,item()可以直接取出数值
放入测试集时

这样子写的目的是要放入一个1*1的矩阵,打印出来也是一个1*1的矩阵


