数据结构（C语言版）-第3章 栈和队列

3.1 栈和队列的定义和特点
3.2 案例引入
3.3 栈的表示和操作的实现
3.4 栈与递归
3.5 队列的的表示和操作的实现
3.6 案例分析与实现

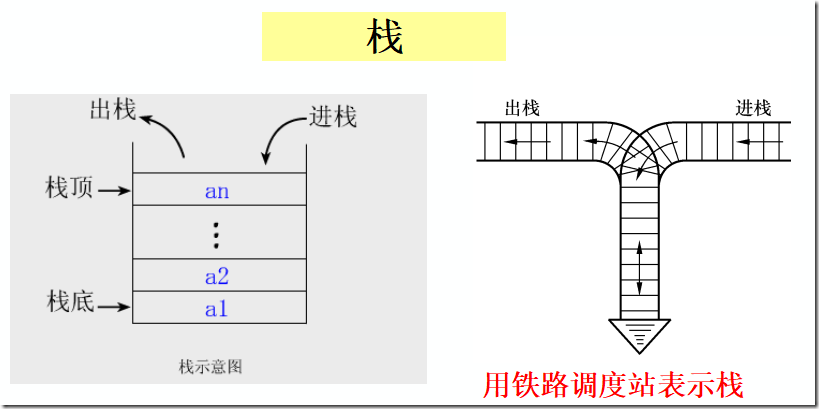
基本操作有入栈、出栈、读栈顶元素值、建栈、判断栈满、栈空等

 

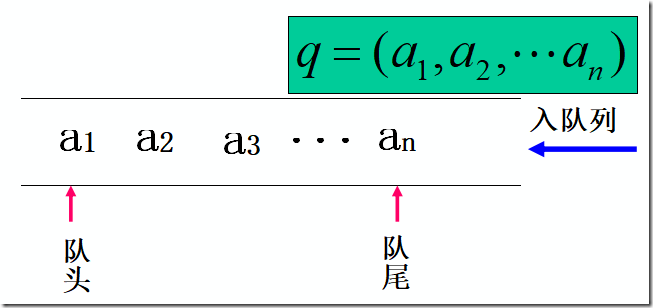
队列是一种先进先出(FIFO) 的线性表. 在表一端插入,在另一端删除

 

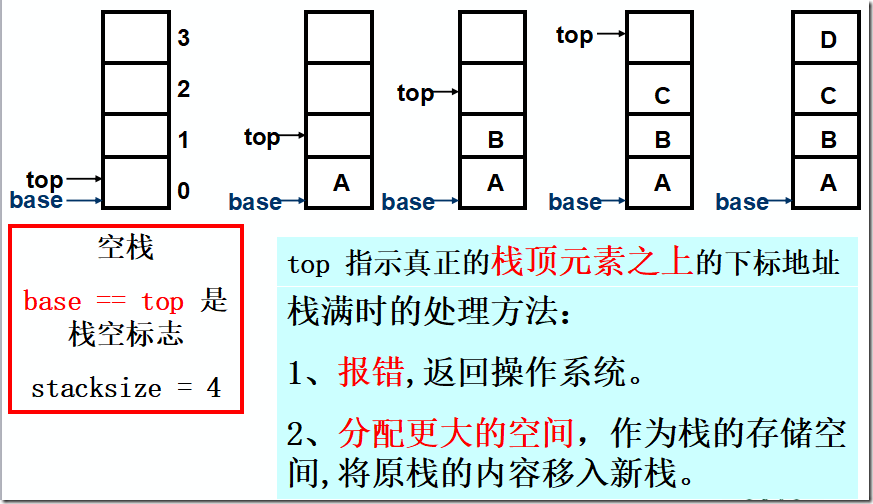
顺序栈的表示

 

顺序栈的定义： 

#define  MAXSIZE  100
typedef struct
{
        SElemType   *base;
        SElemType   *top;
        int stacksize;
}SqStack;

顺序栈初始化

Status InitStack( SqStack &S )
{
    S.base =new SElemType[MAXSIZE]；
    if( !S.base )     return OVERFLOW;  //分配是否成功，分配成功有个地址
    S.top = S.base;
    S.stackSize = MAXSIZE;
    return OK;
}

判断顺序栈是否为空

bool StackEmpty( SqStack S )
{
    if(S.top == S.base) return true;
   else return false;
}

求顺序栈的长度

int StackLength( SqStack S )
{
    return S.top – S.base;
}

清空顺序栈 （还在）

Status ClearStack( SqStack S )
{
    if( S.base ) S.top = S.base;
    return OK;
}

销毁顺序栈

Status DestroyStack( SqStack &S )
{
    if( S.base )
    {
        delete S.base ;
        S.stacksize = 0;
        S.base = S.top = NULL;
    }
  return OK;
}

顺序栈进栈

(1)判断是否栈满，若满则出错
(2)元素e压入栈顶
(3)栈顶指针加1

Status Push( SqStack &S, SElemType e)  
{
    if( S.top - S.base== S.stacksize ) // 栈满
        return ERROR;     
    *S.top++=e;     //*S.top=e;  S.top++;

    return OK;
}

顺序栈出栈

(1)判断是否栈空，若空则出错
(2)获取栈顶元素e
(3)栈顶指针减1

Status Pop( SqStack &S, SElemType &e)  
{
    if( S.top == S.base ) // 栈空
        return ERROR;     
    e＝ *--S.top;    //  --S.top; e=*S.top;

    return OK;
}

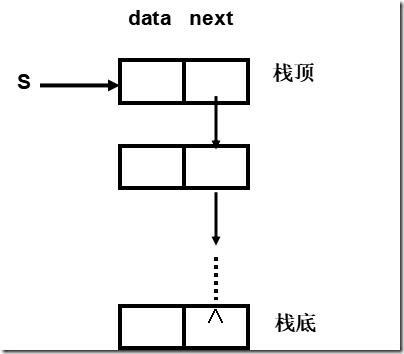
链栈的表示

运算是受限的单链表，只能在链表头部进行操作，故没有必要附加头结点。栈顶指针就是链表的头指针

链栈的定义

typedef  struct StackNode {
      SElemType  data;
      struct StackNode *next;
 } StackNode,  *LinkStack;
LinkStack S;

链栈的初始化

void InitStack(LinkStack &S )
{
    S=NULL;
}

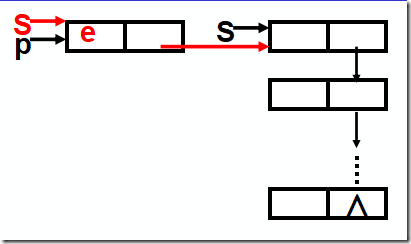
链栈进栈

Status Push(LinkStack &S , SElemType e)
{
  p=new StackNode;      //生成新结点p
  if (!p) exit(OVERFLOW);
  p->data=e; p->next=S; S=p;        

  return OK;
 }

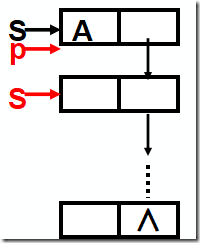
链栈出栈

Status Pop (LinkStack &S,SElemType &e)
{

 if (S==NULL) return ERROR;
 e = S-> data;  p = S;   S =  S-> next;
 delete p;   return OK;  

}

取链栈栈顶元素

SElemType GetTop(LinkStack S)
{
     if (S==NULL) exit(1)；
     else return S–>data;
}

栈与递归

递归的定义  若一个对象部分地包含它自己,  或用它自己给自己定义,  则称这个对象是递归的；若一个过程直接地或间接地调用自己, 则称这个过程是递归的过程。

分治法求解递归问题算法的一般形式：
     void   p (参数表) {
        if   （递归结束条件）可直接求解步骤；-----基本项
        else  p（较小的参数）；------归纳项
       }

优点：结构清晰，程序易读

缺点：每次调用要生成工作记录，保存状态信息，入栈；返回时要出栈，恢复状态信息。时间开销大。

队列的抽象数据类型

     (1)  InitQueue (&Q)         //构造空队列
      (2) DestroyQueue (&Q)   //销毁队列
      (3) ClearQueue (&S)       //清空队列
      (4) QueueEmpty(S)          //判空. 空--TRUE,

     (5) QueueLength(Q)         //取队列长度
      (6) GetHead (Q,&e)         //取队头元素,
      (7) EnQueue (&Q,e)        //入队列
      (8) DeQueue (&Q,&e)     //出队列
      (9) QueueTraverse(Q,visit())       //遍历

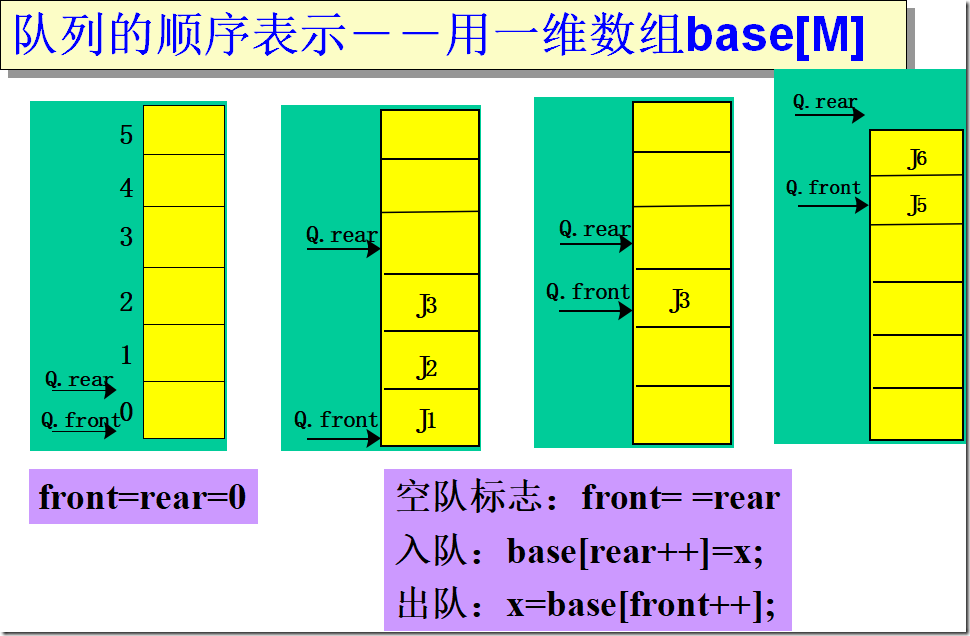
队列的定义

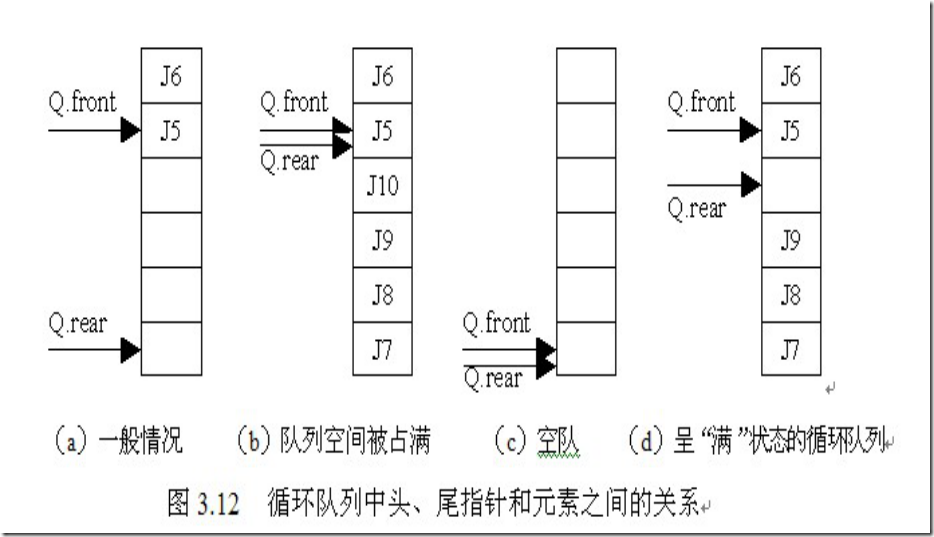
#define M  100   //最大队列长度
Typedef struct {
   QElemType *base;  //初始化的动态分配存储空间
   int  front;            //头指针   
   int  rear;             //尾指针
}SqQueue;

 

循环队列初始化

Status InitQueue (SqQueue &Q){
    Q.base =new QElemType[MAXQSIZE];  //base数组 
   if(!Q.base) exit(OVERFLOW);
    Q.front=Q.rear=0;
    return OK;
}

求循环队列的长度

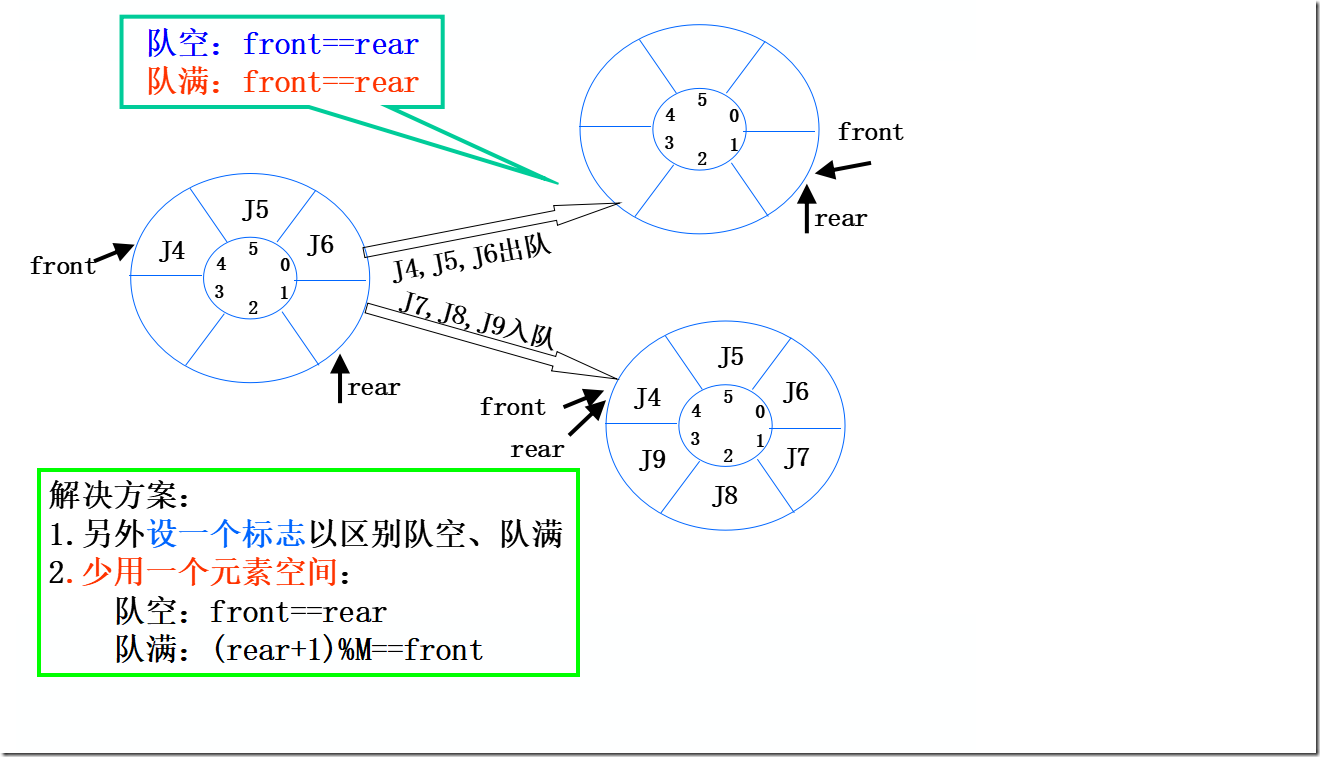
int  QueueLength (SqQueue Q){
    return (Q.rear-Q.front+MAXQSIZE)%MAXQSIZE;                             
}

循环队列入队

Status EnQueue(SqQueue &Q,QElemType e){
    if((Q.rear+1)%MAXQSIZE==Q.front)  return ERROR;
    Q.base[Q.rear]=e;
    Q.rear=(Q.rear+1)%MAXQSIZE;
     return OK;
}

循环队列出队

Status DeQueue (LinkQueue &Q,QElemType &e){
   if(Q.front==Q.rear) return ERROR;
   e=Q.base[Q.front];
   Q.front=(Q.front+1)%MAXQSIZE;
   return OK;
}

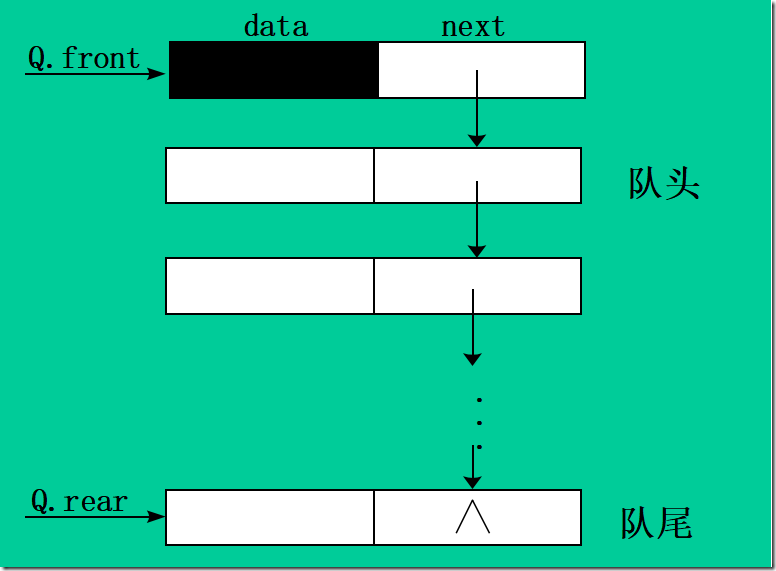
链队列

typedef struct QNode{
   QElemType   data;
   struct Qnode  *next;
}Qnode, *QueuePtr;
typedef struct {
   QueuePtr  front;            //队头指针   
   QueuePtr  rear;             //队尾指针
}LinkQueue;

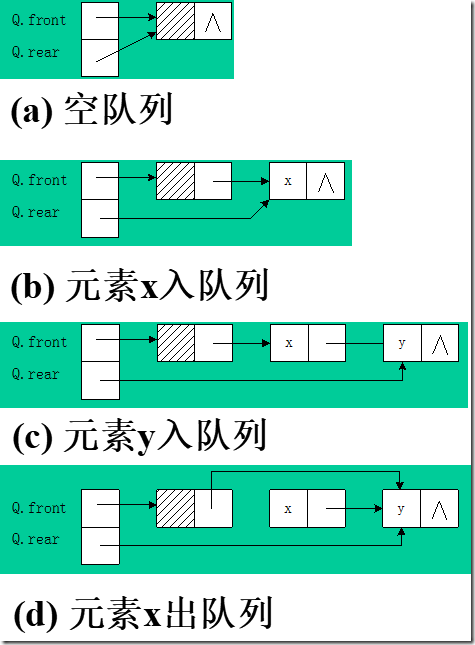
链队列初始化

Status InitQueue (LinkQueue &Q){
   Q.front=Q.rear=(QueuePtr) malloc(sizeof(QNode)); 
    if(!Q.front) exit(OVERFLOW);
    Q.front->next=NULL;
     return OK;
}