Apollo开发者社区-开发者说 | 手把手教你写卡尔曼滤波器
无人驾驶技术入门软件篇已经介绍了传感器数据的解析和传感器信息的坐标转换。
这两步完成后,我们就会获得某一时刻,自车坐标系下的各种传感器数据。
这些数据包括障碍物的位置、速度;
车道线的曲线方程、车道线的类型和有效长度;
自车的GPS坐标等等。
这些信号的组合,表示了无人车当前时刻的环境信息。
由于传感器本身的特性,任何测量结果都是有误差的。
以障碍物检测为例,如果直接使用传感器的测量结果,在车辆颠簸时,可能会造成障碍物测量结果的突变,这对无人车的感知来说是不可接受的。
因此需要在传感器测量结果的基础上,进行跟踪,以此来保证障碍物的位置、速度等信息不会发生突变。
最经典的跟踪算法莫过于卡尔曼在1960年提出的卡尔曼滤波器。
在无人车领域,卡尔曼滤波器除了应用于障碍物跟踪外,也在车道线跟踪、障碍物预测以及定位等领域大展身手。
在介绍卡尔曼滤波器数学原理之前,先从感性上看一下它的工作原理。
简单来讲,卡尔曼滤波器就是根据上一时刻的状态,预测当前时刻的状态,将预测的状态与当前时刻的测量值进行加权,加权后的结果才认为是当前的实际状态,而不是仅仅听信当前的测量值。
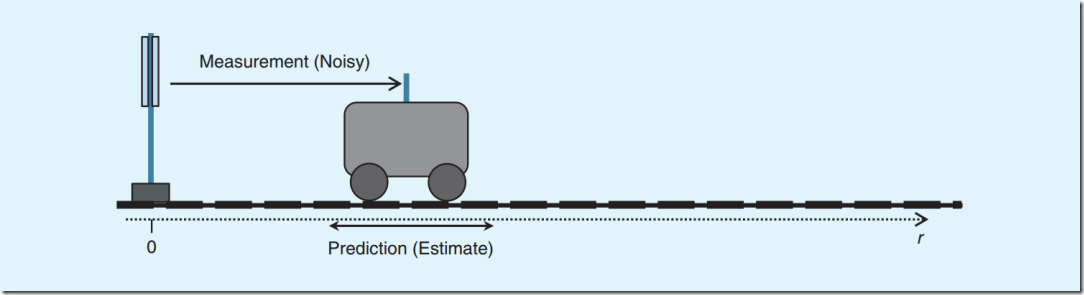
假设有个小车在道路上向右侧匀速运动,我们在左侧安装了一个测量小车距离和速度传感器,传感器每1秒测一次小车的位置s和速度v,如下图所示。
我们用向量xt来表示当前小车的状态,该向量也是最终的输出结果,被称作状态向量(state vector):
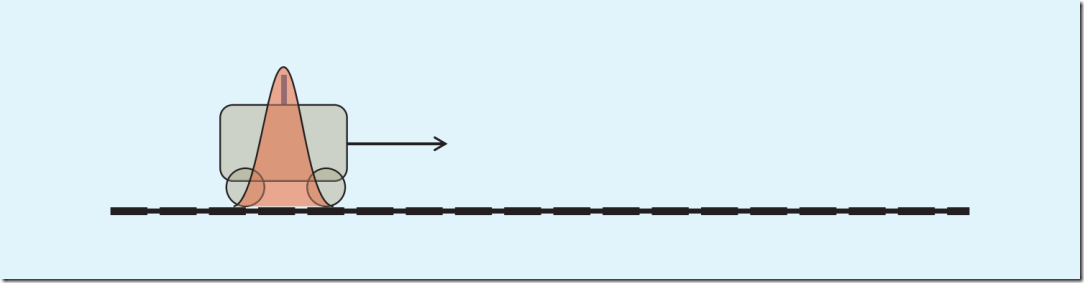
由于测量误差的存在,传感器无法直接获取小车位置的真值,只能获取在真值附近的一个近似值,可以假设测量值在真值附近服从高斯分布。
如下图所示,测量值分布在红色区域的左侧或右侧,真值则在红色区域的波峰处。
由于是第一次测量,没有小车的历史信息,我们认为小车在1秒时的状态x与测量值z相等,表示如下:
公式中的1表示第1秒。
预测是卡尔曼滤波器中很重要的一步,这一步相当于使用历史信息对未来的位置进行推测。
根据第1秒小车的位置和速度,我们可以推测第2秒时,小车所在的位置应该如下图所示。
会发现,图中红色区域的范围变大了,这是因为预测时加入了速度估计的噪声,是一个放大不确定性的过程。
根据小车第一秒的状态进行预测,得到预测的状态xpre:
其中,Pre是Prediction的简称;时间间隔为1秒,所以预测位置为距离+速度*1;由于小车做的是匀速运动,因此速度保持不变。
在第2秒时,传感器对小车的位置做了一次观测,我们认为小车在第2秒时观测值为z2,用向量表示第2秒时的观测结果为:
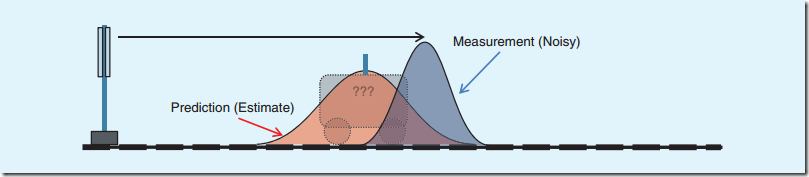
很显然,第二次观测的结果也是存在误差的,我们将预测的小车位置与实际观测到的小车位置放到一个图上,即可看到:
图中红色区域为预测的小车位置,蓝色区域为第2秒的观测结果。
很显然,这两个结果都在真值附近。为了得到尽可能接近真值的结果,我们将这两个区域的结果进行加权,取加权后的值作为第二秒的状态向量。
为了方便理解,可以将第2秒的状态向量写成:
其中,w1为预测结果的权值,w2为观测结果的权值。
两个权值的计算是根据预测结果和观测结果的不确定性来的,这个不确定性就是高斯分布中的方差的大小,方差越大,波形分布越广,不确定性越高,这样一来给的权值就会越低。
加权后的状态向量的分布,可以用下图中绿色区域表示:
你会发现绿色区域的方差比红色区域和蓝色区域的小。
这是因为进行加权运算时,需要将两个高斯分布进行乘法运算,得到的新的高斯分布的方差比两个做乘法的高斯分布都小。
两个不那么确定的分布,最终得到了一个相对确定的分布,这是卡尔曼滤波的一直被推崇的原因。
第1秒的初始化以及第2秒的预测、观测,实现卡尔曼滤波的一个周期。
同样的,我们根据第2秒的状态向量做第3秒的预测,再与第3秒的观测结果进行加权,就得到了第3秒的状态向量;
再根据第3秒的状态向量做第4秒的预测,再与第4秒的观测结果进行加权,就得到了第4秒的状态向量。以此往复,就实现了一个真正意义上的卡尔曼滤波器。
以上就是卡尔曼滤波器的感性分析过程,下面我们回归理性,谈谈如何将以上过程写成代码。
前文用了一个简答的例子对卡尔曼滤波器的整个流程进行了介绍,下面我们根据卡尔曼滤波器的原理,编写代码,跟踪连续的激光雷达点。
在这里就要祭出卡尔曼老先生给我们留下的宝贵财富了,下面7个公式就是卡尔曼滤波器的理性描述,使用下面7个公式,就能够实现一个完整的卡尔曼滤波器。
现在看不懂这7个公式没关系,继续往下看,我会一个一个做解释。
写代码(C++)的过程,实际上就是结合上面的公式,一步步完成初始化、预测、观测的过程。
由于公式中涉及大量的矩阵转置和求逆运算,我们使用开源的矩阵运算库——Eigen库。
在Initialization这一步,需要将各个变量初始化,对于不同的运动模型,其状态向量肯定是不一样的,
比如前文小车的例子,只需要一个距离s和一个速度v就可以表示小车的状态;
再比如在一个2维空间中的点,需要x方向上的距离和速度以及y方向上的距离和速度才能表示,这样的状态方程就有4个变量。
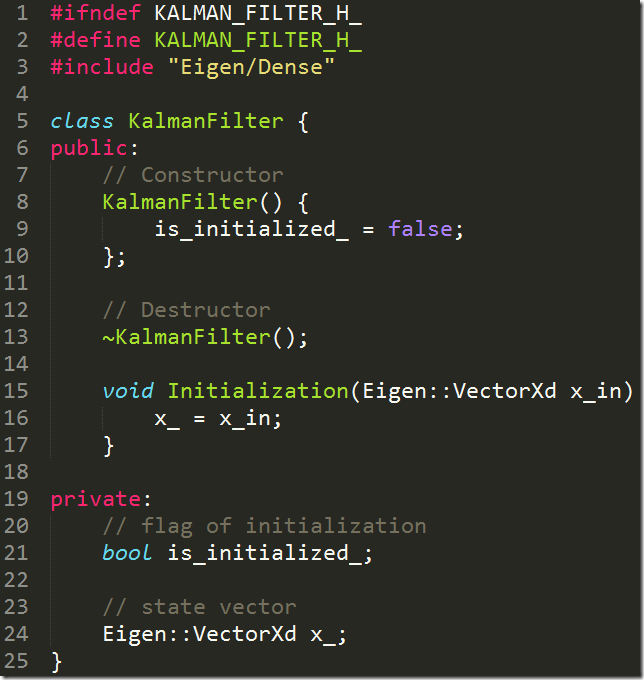
因此我们使用Eigen库中非定长的数据结构,下图中的VerctorXd表示X维的列矩阵,其中的元素数据类型为double。
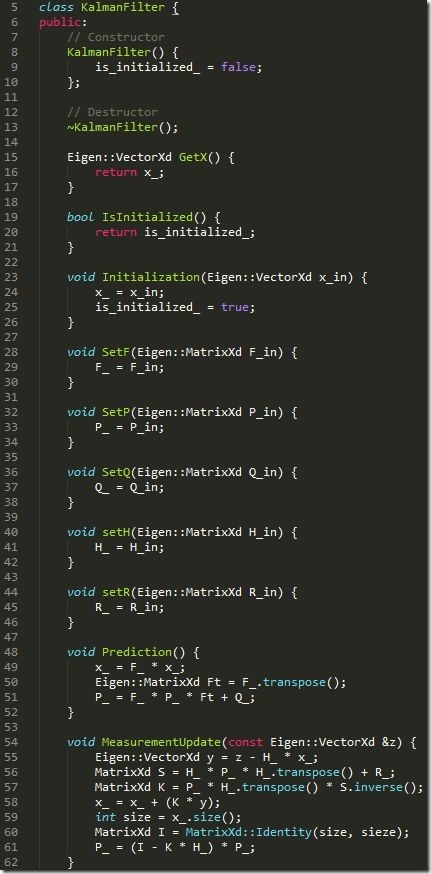
在这里,我们新建了一个KalmanFilter类,其中定义了一个叫做x_的变量,表示这个卡尔曼滤波器的状态向量。
完成初始化后,我们开始写Prediction部分的代码。首先是公式
这里的x为状态向量,通过左乘一个矩阵F,再加上外部的影响u,得到预测的状态向量x'。这里的F成为状态转移矩阵(state transistion matrix)。
以2维的匀速运动为例,这里的x为
对于匀速运动模型,根据中学物理课本中的公式s1 = s0 + vt,经过时间△t后的预测状态向量应该是
由于假设当前运动为匀速运动,加速度为0,加速度不会对预测造成影响,即
如果换成加速或减速运动模型,就可以引入加速度a_x和a_y,根据s1 = s0 + vt + at^2/2这里的u会变成:
作为入门课程,这里不讨论太复杂的模型,因此公式
最终将写成
由于每次做预测时,△t的大小不固定,因此我们专门写一个函数SetF()
再看预测模块的第二个公式
该公式中P表示系统的不确定程度,这个不确定程度,在卡尔曼滤波器初始化时会很大,随着越来越多的数据注入滤波器中,不确定程度会变小,P的专业术语叫状态协方差矩阵(state covariance matrix);
这里的Q表示过程噪声(process covariance matrix),即无法用x'=Fx+u表示的噪声,比如车辆运动时突然到了上坡,这个影响是无法用之前的状态转移估计的。
以激光雷达为例。激光雷达只能测量点的位置,无法测量点的速度,因此对于激光雷达的协方差矩阵来说,对于位置信息,其测量位置较准,不确定度较低;
对于速度信息,不确定度较高。因此可以认为这里的P为:
由于Q对整个系统存在影响,但又不能太确定对系统的影响有多大。工程上,我们一般将Q设置为单位矩阵参与运算,即
根据以上内容和公式
我们就可以写出预测模块的代码了
实际编程时x'及P'不需要申请新的内存去存储,使用原有的x和P代替即可。
观测的第一个公式是
这个公式计算的是实际观测到的测量值z与预测值x'之间差值y。
不同传感器的测量值一般不同,比如激光雷达测量的位置信号为x方向和y方向上的距离,毫米波雷达测量的是位置和角度信息。
因此需要将状态向量左乘一个矩阵H,才能与测量值进行相应的运算,这个H被称为测量矩阵(Measurement Matrix)。
激光雷达的测量值为
其中xm和ym分别表示x方向上的测量(measurement)值。
由于x'是一个4*1的列向量,如果要与一个2*1的列向量z进行减运算,需要左乘一个2*4的矩阵才行,因此整个公式最终要写成:
即,对于激光雷达来说,这里的测量矩阵H为
求得y值后,对y值乘以一个加权量,再加到原来的预测量上去,就可以得到一个既考虑了测量值,又考虑了预测模型的位置的状态向量了。
那么y的这个权值该如何取呢?
再看接下里的两个公式
这两个公式求的是卡尔曼滤波器中一个很重要的量——卡尔曼增益K(Kalman Gain),用人话讲就是求y值的权值。
第一个公式中的R是测量噪声矩阵(measurement covariance matrix),这个表示的是测量值与真值之间的差值。一般情况下,传感器的厂家会提供该值。
S只是为了简化公式,写的一个临时变量,不要太在意。
看最后两个公式
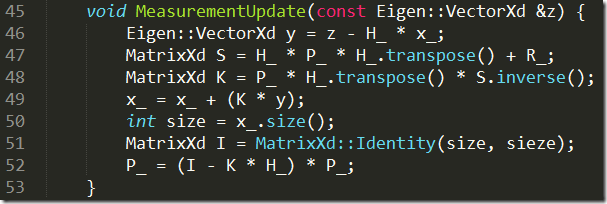
这两个公式,实际上完成了卡尔曼滤波器的闭环,第一个公式是完成了当前状态向量x的更新,不仅考虑了上一时刻的预测值,也考虑了测量值,和整个系统的噪声,
第二个公式根据卡尔曼增益,更新了系统的不确定度P,用于下一个周期的运算,该公式中的I为与状态向量同维度的单位矩阵。
将以上五个公式写成代码如下:
至此,一个卡尔曼滤波器的雏形就出来了。
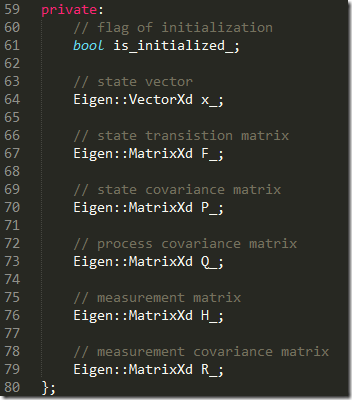
包含的变量有:
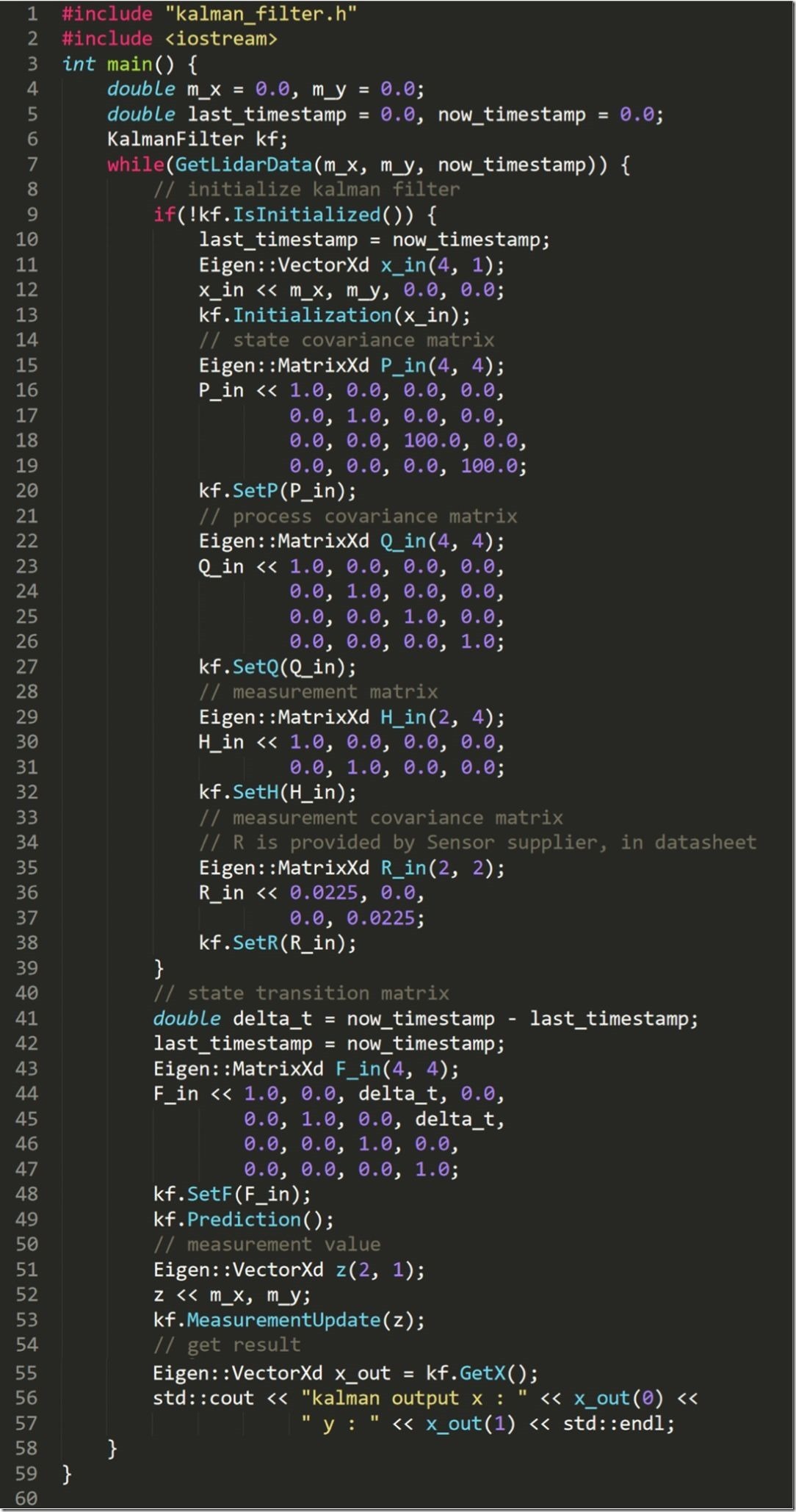
以激光雷达数据为例,使用以上滤波器,代码如下:
其中GetLidarData函数除了获取点的位置信息m_x和m_y外,还获取了当前时刻的时间戳,用于计算前后两帧的时间差delta_t。
以上就是卡尔曼滤波器对于匀速运动物体跟踪的例子。
在这个基础上,业内还有扩展卡尔曼滤波器和无迹卡尔曼滤波器,它们与经典卡尔曼滤波器的最大区别是状态转移矩阵F和测量矩阵H的不同,剩下的跟踪过程依然需要使用前面介绍的7个公式。
只要你能够写出某个模型的F、P、Q、H、R矩阵,任何状态跟踪的问题都将迎刃而解。



![clip_image002[4] clip_image002[4]](https://img2018.cnblogs.com/blog/1556226/201902/1556226-20190213103011058-1241115310.jpg)

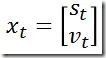
![clip_image007[4] clip_image007[4]](https://img2018.cnblogs.com/blog/1556226/201902/1556226-20190213103017391-325852190.jpg)


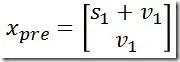

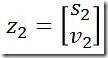
![clip_image015[4] clip_image015[4]](https://img2018.cnblogs.com/blog/1556226/201902/1556226-20190213103029198-760523576.png)
![clip_image016[4] clip_image016[4]](https://img2018.cnblogs.com/blog/1556226/201902/1556226-20190213103030012-2075631117.jpg)
![clip_image017[4] clip_image017[4]](https://img2018.cnblogs.com/blog/1556226/201902/1556226-20190213103031232-1660020474.jpg)

![clip_image003[1] clip_image003[1]](https://img2018.cnblogs.com/blog/1556226/201902/1556226-20190213103032992-539710881.jpg)
![clip_image020[4] clip_image020[4]](https://img2018.cnblogs.com/blog/1556226/201902/1556226-20190213103034505-1309851350.jpg)
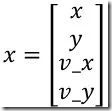
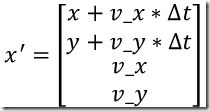
![clip_image025[4] clip_image025[4]](https://img2018.cnblogs.com/blog/1556226/201902/1556226-20190213103037426-55096294.jpg)

![clip_image027[4] clip_image027[4]](https://img2018.cnblogs.com/blog/1556226/201902/1556226-20190213103039575-2084986159.jpg)
![clip_image029[4] clip_image029[4]](https://img2018.cnblogs.com/blog/1556226/201902/1556226-20190213103040798-1880690786.png)

![clip_image031[4] clip_image031[4]](https://img2018.cnblogs.com/blog/1556226/201902/1556226-20190213103041916-1418077096.jpg)
![clip_image032[4] clip_image032[4]](https://img2018.cnblogs.com/blog/1556226/201902/1556226-20190213103043157-1468838926.jpg)
![clip_image033[4] clip_image033[4]](https://img2018.cnblogs.com/blog/1556226/201902/1556226-20190213103044188-1238322967.jpg)
![clip_image035[4] clip_image035[4]](https://img2018.cnblogs.com/blog/1556226/201902/1556226-20190213103045515-160606852.jpg)
![clip_image036[4] clip_image036[4]](https://img2018.cnblogs.com/blog/1556226/201902/1556226-20190213103046168-489704433.png)