试题 历届试题 密码脱落(区间dp)

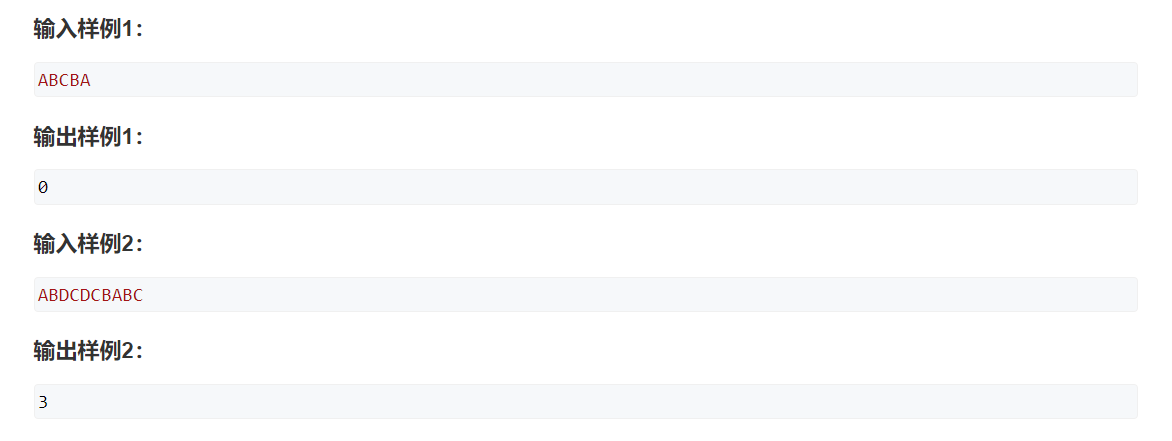
题解:题目大意是添加最少几个字符使得该串变为回文串,这里可以转化为最少删除几个字符成为回文串(删除字符和添加字符其实一样);
那么问题的答案就是总长度减去最长回文串(子序列)的长度。
求解最长回文子序列长度使用区间dp来求解。
状态表示f[l][r]表示r-l区间内最长回文子序列的长度。属性值是最大值。
集合的划分,分为四种情况
1.l和r都在最长回文串当中,有f[l+1][r-1]+2;
2.l在最长回文串当中,r不在
3.r在最长回文串当中,l不在
4.l、r都不在最长回文串当中
对于情况2和3,需要一个点保证不取到,而我们的状态表示f[i][j]并不保证i和j的取或者不取。
这里比较巧妙的是集合存放的是最大值,那么这其中子集有重复的情况并不影响最后的结果。
所以对于情况2,可以用f[l][r-1]来表示(包含关系),对于情况3,可以用f[l+1][r-1]来表示(包含关系);
而对于情况4,已经被包含在情况2和3的状态之中。
那么我们只需要讨论情况1、2、3之中的最大值即是当前区间的最大值。
#include<bits/stdc++.h> using namespace std; int f[1005][1005]; int main(){ string s;cin>>s; for(int len=1;len<=s.size();len++){ for(int l=0;l+len-1<s.size();l++){ int r=l+len-1; if(l==r){f[l][r]=1;continue;} else if(s[l]==s[r]){ f[l][r]=max(f[l][r],f[l+1][r-1]+2); } f[l][r]=max(f[l][r],max(f[l][r-1],f[l+1][r])); } } cout<<s.size()-f[0][s.size()-1]<<endl; return 0; }
