1050. 鸣人的影分身(dp)

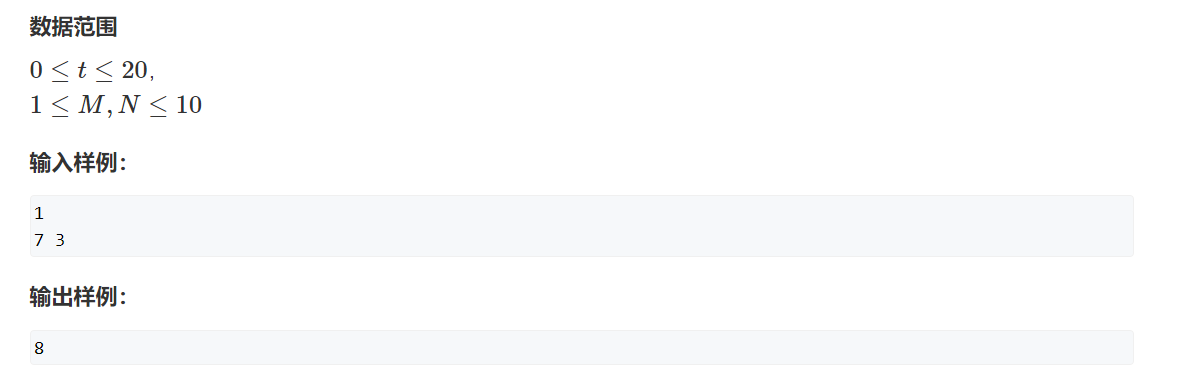
题解:整数划分问题。将M划分为最多N个数的所有方案数。比较经典的题,dp的划分方式想不出,这里记录一下。
f[i][j]表示总和为i,划分为了j个数的方案。集合可以划分为两个部分
1.序列中存在数字0,那么f[i][j]=f[i][j-1](相当于可以减少一个划分数)
2.序列数不存在0,即都大于等于1,那么可以将每个数减一,得到的映射的方案数也是该序列的方案数f[i][j]=f[i-j][j](i>=j)
所以总的方案数f[i][j]=f[i][j-1]+f[i-j][j];初始化f[0][0]=1;算法复杂度o(n^2);
#include<bits/stdc++.h> using namespace std; const int N = 25; int f[N][N]; int t,m,n; int main(){ scanf("%d",&t); for(int i=0;i<t;i++){ memset(f,0,sizeof(f)); scanf("%d%d",&m,&n); f[0][0]=1; for(int i=0;i<=m;i++){ for(int j=1;j<=n;j++){ f[i][j]+=f[i][j-1]; if(i>=j)f[i][j]+=f[i-j][j]; } } cout<<f[m][n]<<endl; } return 0; }

 浙公网安备 33010602011771号
浙公网安备 33010602011771号