1295. X的因子链(线性筛、算术基本定理)

传送门

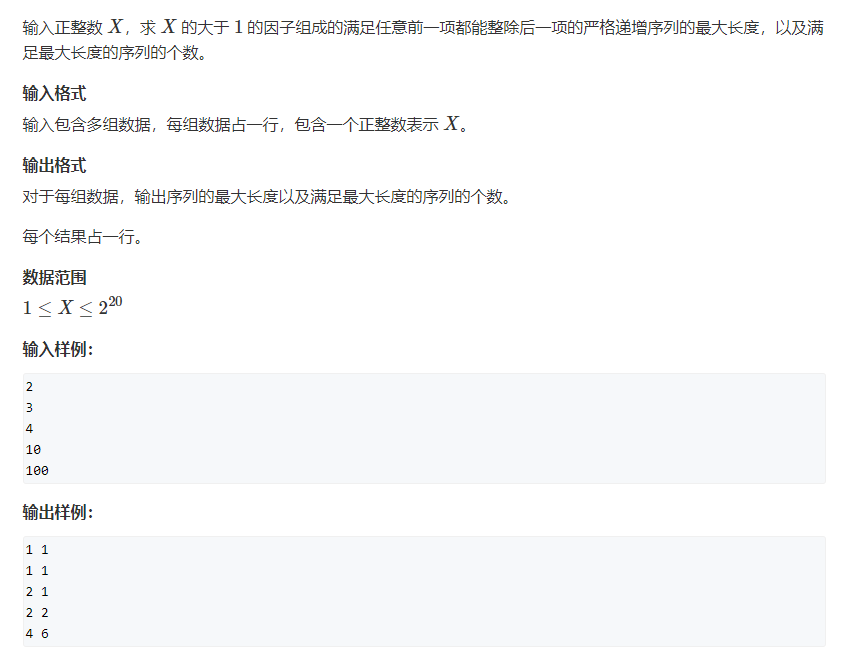
前置知识:算术基本定理:任何一个大于1的自然数 N,如果N不为质数，那么N可以唯一分解成有限个质数的乘积N=P1^a1*P2^a2*P3^a3......Pn^an，这里P1<P2<P3......<Pn均为质数，其中指数ai是正整数。

题解:由算术基本定理，我们可以将x拆成若干个质数相乘，那么就可以将这些最小质因子进行排列组合相乘得到的递增序列，满足了题意要求因子后一项整除前一项，则其最大长度是每一项的指数之和(a1+a2....+an)，方案数是(a1+a2....+an)!/(a1!*a2!*....*an!)(相同的数调换位置排列结果一样)

最小质因子可以用线性筛，数据范围是2^20次方，最大的排列数是20!在long long 范围以内，可以用longlong存储。

#include<bits/stdc++.h>
using namespace std;
const int N = 1050005;
int prime[N],st[N],min_p[N],sum[N];
int cnt;
void get_prime(int n){
    for(int i=2;i<=n;i++){
        if(!st[i]){
            prime[cnt++]=i;
            min_p[i]=i;
            st[i]=1;
        }
        for(int j=0;j<cnt&&prime[j]*i<=n;j++){
            if(!st[prime[j]*i]){
                min_p[i*prime[j]]=prime[j];
                st[prime[j]*i]=1;
            }
            if(i%prime[j]==0)break;
        }
    }
}
int main(){
    int x,tot;
    get_prime(N-1);//线性筛
    while(scanf("%d",&x)!=-1){
        int n=x;
        tot=0;
        long long ans=1,res=1;
        int k=0;
        while(x!=1){
            //cout<<"*"<<min_p[x]<<"*"<<endl;
            ///注意这里每组数据是1e6,最多有100组数据，不可以memset去清空sum数组。
            sum[k]=0;//记录每个质因子的指数
            int p=min_p[x];//当前x的最小质因子
            while(x%p==0){
                sum[k]++;
                ans*=sum[k];//ans存储指数的排列相乘 
                x/=p;
                tot++;
                res*=tot;
            }
            k++;
        }
        cout<<tot<<" "<<res/ans<<endl;
    }
    return 0;
}