11道背包问题
1.01背包
#include<bits/stdc++.h>
using namespace std;
const int N=1005;
int f[N];
int n,V,v,w;
int main(){
cin>>n>>V;
for(int i=0;i<n;i++){
cin>>v>>w;
for(int j=V;j-v>=0;j--){
f[j]=max(f[j],f[j-v]+w);
}
}
cout<<f[V]<<endl;
return 0;
}
2.完全背包
#include<bits/stdc++.h>
using namespace std;
const int N=1005;
int n,V,v,w;
int f[N];
int main(){
cin>>n>>V;
for(int i=0;i<n;i++){
cin>>v>>w;
for(int j=0;j<=V;j++){
if(j-v>=0)f[j]=max(f[j],f[j-v]+w);
}
}
cout<<f[V]<<endl;
return 0;
}
3. 多重背包问题 I 普通写法o(n^3)
#include<bits/stdc++.h>
using namespace std;
const int N=1005;
int n,V,v,w,s;
int f[N];
int main(){
cin>>n>>V;
for(int i=0;i<n;i++){
cin>>v>>w>>s;
for(int j=V;j>=0;j--){
for(int k=1;k<=s;k++){
if(j-k*v>=0)f[j]=max(f[j],f[j-k*v]+k*w);
}
}
}
cout<<f[V]<<endl;
return 0;
}
4.多重背包问题 II 二进制拆分o(n^2logs)
#include<bits/stdc++.h>
using namespace std;
const int N=4000005;
int n,V,v,w,s;
int f[N],a[N],b[N];
int main(){
int cnt=1,m;
cin>>n>>V;
for(int i=0;i<n;i++){
cin>>v>>w>>s;
for(int j=1;j<=s;j<<=1){
b[cnt]=j*w;
a[cnt++]=j*v;
s-=j;
}
if(s>0){
b[cnt]=s*w;
a[cnt++]=s*v;
}
}
for(int i=1;i<cnt;i++){
for(int k=V;k>=0;k--){
if(k-a[i]>=0){
f[k]=max(f[k],f[k-a[i]]+b[i]);
}
}
}
cout<<f[V]<<endl;
return 0;
}
5.多重背包问题 III 单调队列(困难,待补坑)

6.混合背包问题

#include<bits/stdc++.h>
using namespace std;
const int N = 1005;
int a[N*N],b[N*N],c[N*N],f[N];
int main(){
int n,v,inf=0;
cin>>n>>v;
for(int i=0;i<n;i++){
int v,w,s;
cin>>v>>w>>s;
if(!s){//完全
a[inf]=v;
b[inf]=w;
c[inf++]=0;
}
else{
if(s==-1){
a[inf]=v;
b[inf]=w;
c[inf++]=1;//01
}
else{//多重背包
int k=1;
while(k<=s){
a[inf]=k*v;
b[inf]=k*w;
c[inf++]=1;
s-=k;
k<<=1;
}
if(s){
a[inf]=s*v;
b[inf]=s*w;
c[inf++]=1;
}
}
}
}
for(int i=0;i<inf;i++){
if(c[i]==0){
for(int j=a[i];j<=v;j++){
f[j]=max(f[j],f[j-a[i]]+b[i]);
}
}
else{
for(int j=v;j>=a[i];j--){
f[j]=max(f[j],f[j-a[i]]+b[i]);
}
}
}
cout<<f[v]<<endl;
return 0;
}
7. 二维费用的背包问题
满足体积和重量两种要求
#include<bits/stdc++.h>
using namespace std;
const int N = 1005;
int f[N][N];
int a[N],b[N],c[N];
int main(){
int n,v,m;
cin>>n>>v>>m;
for(int i=0;i<n;i++){
int v,m,w;
cin>>v>>m>>w;
a[i]=v,b[i]=m,c[i]=w;
}
for(int i=0;i<n;i++){
for(int j=v;j>=a[i];j--){
for(int z=m;z>=b[i];z--){
f[j][z]=max(f[j][z],f[j-a[i]][z-b[i]]+c[i]);
}
}
}
cout<<f[v][m]<<endl;
return 0;
}
8. 分组背包问题

#include<bits/stdc++.h>
using namespace std;
const int N = 1005;
int f[N];
int a[N][N],b[N][N],c[N];
int main(){
int n,v,m,inf=0;
cin>>n>>v;
for(int i=0;i<n;i++){
int s,v,w;
cin>>s;
c[i]=s;
for(int j=0;j<s;j++){
cin>>v>>w;
a[i][j]=v,b[i][j]=w;
}
}
for(int i=0;i<n;i++){
for(int j=v;j>=0;j--){
for(int k=0;k<c[i];k++){
if(j>=a[i][k]){
f[j]=max(f[j],f[j-a[i][k]]+b[i][k]);
}
}
}
}
cout<<f[v]<<endl;
return 0;
}
9. 有依赖的背包问题
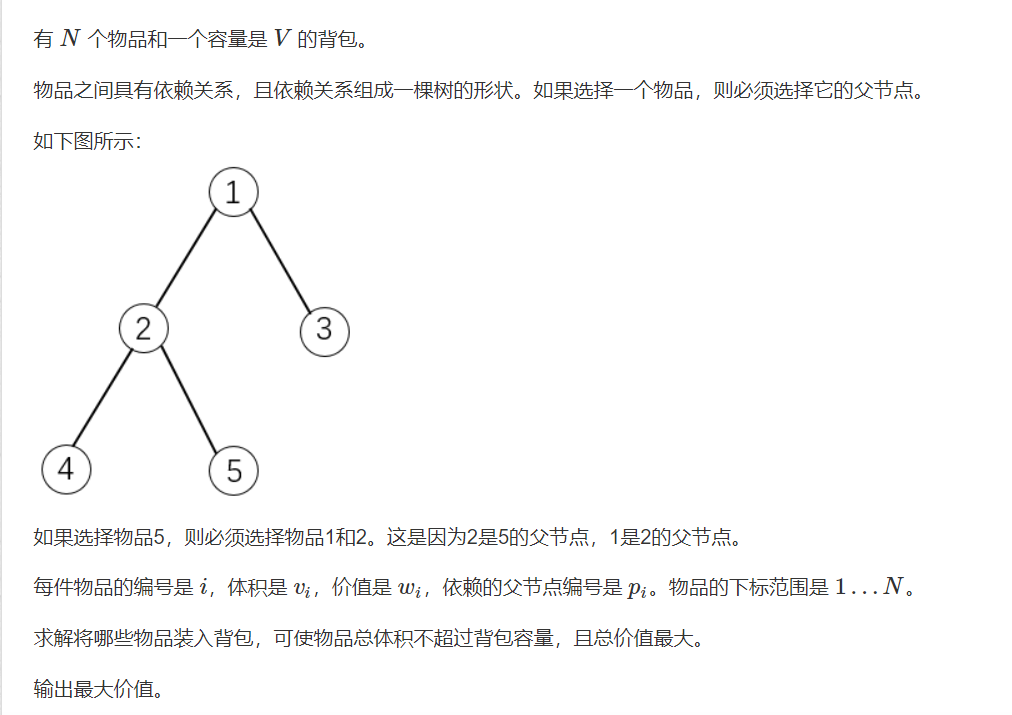

#include<bits/stdc++.h>
using namespace std;
const int N = 1005;
vector<int>a[N];
int n,m,root,son;
int v[N],w[N];
int f[N][N];///代表当前节点u最大体积为v的最大价值
void dfs(int u){
for(int i=v[u];i<=m;i++){
f[u][i]=w[u];///根节点的值先赋值
}
for(int i=0;i<a[u].size();i++){///枚举子树
int son=a[u][i];
dfs(son);///递归子树
for(int j=m;j>=v[u];j--){///从大到小枚举(01背包),j必须大于v[u]才能存放根节点
for(int k=0;k<=j-v[u];k++){///k是留给子树的容量,k必须小于等于j-v[u]才能保证根节点能存放
f[u][j]=max(f[u][j],f[u][j-k]+f[son][k]);
}
}
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
int V,W,p;
cin>>V>>W>>p;
if(p==-1){
root=i;
v[root]=V;
w[root]=W;
}
else{
a[p].push_back(i);
v[i]=V;
w[i]=W;
}
}
dfs(root);
cout<<f[root][m]<<endl;
return 0;
}
10.背包问题求方案数
#include<bits/stdc++.h>
using namespace std;
const int N = 1005;
const int mod = 1e9+7;
int f[N],g[N];
int main(){
int n,m;
cin>>n>>m;
g[0]=1;///初始化
for(int i=0;i<n;i++){
int v,w;
cin>>v>>w;
for(int j=m;j>=v;j--){
int s=0;///当前最优价值的方案数
int t=max(f[j],f[j-v]+w);
if(t==f[j])s+=g[j];///最大值是f[j]
if(t==f[j-v]+w)s+=g[j-v];///也可以是两者值相等,则方案数相加
f[j]=t;
g[j]=s;///更新
g[j]%=mod;
}
}
int maxx=-1;
for(int i=0;i<=m;i++){
maxx=max(maxx,f[i]);///取出最大价值
}
int res=0;
for(int i=0;i<=m;i++){
if(f[i]==maxx){///判断当前体积能否达到最大价值,可以就加上方案数
res+=g[i];
}
res%=mod;
}
cout<<res<<endl;
return 0;
}
11.背包问题求具体方案,要求输出字典序最小的具体方案

#include<bits/stdc++.h>
using namespace std;
const int N = 1005;
const int mod = 1e9+7;
int f[N][N];///f[i][j]代表第i个元素到最后元素的最大价值
int v[N],w[N];
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>v[i]>>w[i];
}
for(int i=n;i>=1;i--){///从后往前,最后得到的f[1][m]是1到n的最大价值
for(int j=0;j<=m;j++){
f[i][j]=f[i+1][j];
if(j>=v[i]){
f[i][j]=max(f[i+1][j],f[i+1][j-v[i]]+w[i]);
}
}
}
int s=m;
for(int i=1;i<=n;i++){///字典序要尽量小,则从前往后找
if(v[i]<=s&&f[i][s]==f[i+1][s-v[i]]+w[i]){///如果第i个被选中
printf("%d ",i);
s-=v[i];///减掉该物品的体积
}
if(s<=0)break;
}
return 0;
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号