欧拉函数
定义
在数论,对正整数n,欧拉函数是小于或等于n的正整数中与n互质的数的数目。符号为φ(x)。例如φ(8)=4,因为1,3,5,7均和8互质。
通式
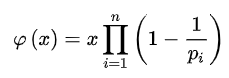 , (其中p1, p2……pn为x的所有质因数,x是不为0的整数)
, (其中p1, p2……pn为x的所有质因数,x是不为0的整数)
性质1.
对于质数n,φ(n) = n−1
性质2.
欧拉函数是积性函数,积性函数是对于任意互质的整数a和b有性质f(ab)=f(a)⋅f(b)的数论函数。
若m,n互质,φ(mn) = φ(m)⋅φ(n),当n为奇质数时,φ(2n)=φ(2)⋅φ(n)=n; 因为2与奇数一定互质。
性质3.
若p为质数,则φ(p^k) = p^k−p^k−1
因为与p^k互质的只有p的倍数,而p^k中p的倍数有p^k−1个。
性质5.
小于n且与n互质的数的和:S = n∗φ(n)/2
性质6.
对于质数p,当n mod p = 0,有φ(n∗p) = φ(n)∗p;eg φ(100)=5*φ(20)=5*8=40;
n mod p ≠ 0,有φ(n∗p) = φ(n)∗(p−1);
性质7.
欧拉反演
n=∑d|nφ(d)即n的因数((包括1和它自己))的欧拉函数之和等于n。
eg.8的因子有1,2,4,8,即φ(1)+φ(2)+φ(4)+φ(8)=8;
算法代码部分
求单个欧拉函数值 朴素的写法o(logn)
#include<bits/stdc++.h>
using namespace std;
int main(){
long long int sum,n;
cin>>n;
sum=n;
for(int i=2;i<=sqrt(n);i++){
if(n%i==0){
sum=sum*(i-1)/i;
while(n%i==0){///把i的倍数删干净
n/=i;
}
}
}
if(n>1)sum=sum*(n-1)/n;///如果n大于1,最后还需要把n这个数算进去
cout<<sum<<endl;
return 0;
}
如果我们用上面方法求n个欧拉函数,结果是o(n*logn)。
更快的方法是欧氏筛求欧拉函数值。
///同时求质数和欧拉函数值
#include<bits/stdc++.h>
using namespace std;
const int maxn=10005;
int phi[maxn],prime[maxn],cnt;
bool flag[maxn];///0为质数,1为合数。
void getphi(int n){
phi[1]=1;
for(int i=2;i<=n;i++){
if(!flag[i]){
prime[++cnt]=i;
phi[i]=i-1;///i是质数
}
for(int j=1;j<=cnt&&i*prime[j]<=n;j++){
flag[i*prime[j]]=1;///标记为合数
if(i%prime[j]==0){
phi[i*prime[j]]=phi[i]*prime[j];
///对于i%j=0,j是质数,有phi(i*j)=phi(i)*j;
break;
}
else{
phi[i*prime[j]]=phi[i]*(prime[j]-1);
///gcd(i,j)=1,j是质数;phi(i*j)=phi(i)*phi(j)=phi(i)*(j-1);
}
}
}
}
int main(){
int n;
cin>>n;
getphi(n);
for(int i=1;i<=n;i++){
cout<<i<<" "<<phi[i]<<endl;
}
return 0;
}
欧拉筛中有一行代码
if(i%prime[j]==0)break;
个人理解是当i是prime[j]的倍数,那么如果不跳出当前循环,下一轮执行的是flag[ i*prime[j+1] ]=1,而 i=k*prime[j], i*prime[j+1]=k*prime[j]*prime[k+1]= k’*prime[j];
即这个合数会被更大的数乘以prime[j]筛掉,如果此时用prime[j+1]筛掉,就造成了重复筛。接下去的质数同理,所以此时不用继续筛下去。因此,在满足i%prime[j]==0这个条件之前以及第一次满足该条件时,prime[j]必定是prime[j]*i的最小因子。
我们应该保证每个合数都只会被它的最小素因子筛掉,就把复杂度降到了O(N)。

