试题 历届试题 斐波那契(矩阵快速幂)

问题描述

　　斐波那契数列大家都非常熟悉。它的定义是：

　　f(x) = 1 .... (x=1,2)
　　f(x) = f(x-1) + f(x-2) .... (x>2)

　　对于给定的整数 n 和 m，我们希望求出：
　　f(1) + f(2) + ... + f(n) 的值。但这个值可能非常大，所以我们把它对 f(m) 取模。
　　公式如下


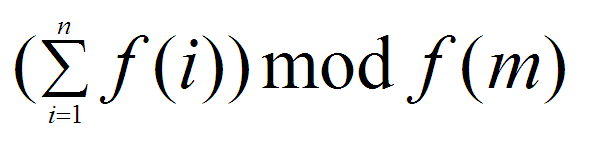
　　但这个数字依然很大，所以需要再对 p 求模。

输入格式

　　输入为一行用空格分开的整数 n m p (0 < n, m, p < 10^18)

输出格式

　　输出为1个整数，表示答案

样例输入

2 3 5

样例输出

0

样例输入

15 11 29

样例输出

25

思路

由规模知要使用矩阵快速幂，前n项斐波那契和有sum=f[n+2]-1;(把每一项拆成两项相减，前后抵消)，则问题转化为求f[n+2]%f[m]%p；

再利用构造矩阵递推第n+2项的值，但是此代码只有60分，最后两个点没过，看了很久没找出来，先放着吧

#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long int ll;
struct mat{
    ll m[3][3];
}unit;
ll n,m,p,mod;
ll ksm(ll a1,ll a2){///快速乘法中间取模防止溢出
    ll res=0;
    if(a1>a2)swap(a1,a2);
    while(a2!=0){
        if(a2&1){res=(res+a1)%mod;}
        a1=(a1+a1)%mod;
        a2>>=1;
    }
    return res;
}
mat mul(mat a1,mat a2){
    mat temp;
    //memset(temp.m,0,sizeof(temp.m));
    for(int i=1;i<=2;i++){
        for(int j=1;j<=2;j++){
                temp.m[i][j]=0;
                for(int k=1;k<=2;k++){
                temp.m[i][j]=(temp.m[i][j]+ksm(a1.m[i][k],a2.m[k][j]))%mod;
            }
        }
    }
    return temp;
}
int quick_mat(ll n){
    mat ans;
    memset(ans.m,0,sizeof(ans.m));
    for(int i=1;i<=2;i++)ans.m[i][i]=1;
    unit.m[1][1]=1;unit.m[1][2]=1;unit.m[2][1]=1;unit.m[2][2]=0;
    while(n!=0){
        if(n&1)ans=mul(ans,unit);
        unit=mul(unit,unit);
        n>>=1;
    }
    return ans.m[1][2]%mod;///第一行第二列为f[n]
}

int main(){
    ll sum=0;
    cin>>n>>m>>p;
    if(n+2<=m){///若n+2<=m 则无需对m进行取模,直接对p取模
        mod=p;
        cout<<(quick_mat(n+2)-1)%p<<endl;
        return 0;
    }
    mod=-1;
    mod=quick_mat(m);///先算出f(m)
    sum=quick_mat(n+2);
    cout<<(sum-1)%p<<endl;
    return 0;
}

 

洛谷也有类似题P1349

传送门

思路和普通斐波那契大同小异，稍微变动一下构造矩阵的值即可。

#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
struct mat{
    ll m[3][3];
}unit;
ll p,q,a1,a2,n,m,mod;
mat mul(mat a1,mat a2){
    mat temp;
    //memset(temp.m,0,sizeof(temp.m));
    for(int i=1;i<=2;i++){
        for(int j=1;j<=2;j++){
                temp.m[i][j]=0;
            for(int k=1;k<=2;k++){
                temp.m[i][j]=(temp.m[i][j]+(a1.m[i][k]*a2.m[k][j])%mod)%mod;
            }
        }
    }
    return temp;
}
int quick_mat(ll n){
    mat ans;
    memset(ans.m,0,sizeof(ans.m));
    for(int i=1;i<=2;i++)ans.m[i][i]=1;
    n-=2;
    while(n!=0){
        if(n&1)ans=mul(ans,unit);
        unit=mul(unit,unit);
        n>>=1;
    }
    mat t;
    t.m[1][1]=a2,t.m[1][2]=0,t.m[2][1]=a1,t.m[2][2]=0;
    ans=mul(ans,t);
    return ans.m[1][1];
}

int main(){
    cin>>p>>q>>a1>>a2>>n>>mod;
    unit.m[1][1]=p;unit.m[1][2]=q;unit.m[2][1]=1;unit.m[2][2]=0;
    cout<<quick_mat(n)<<endl;
    return 0;
}