试题 历届试题 九宫重排(bfs)

问题描述

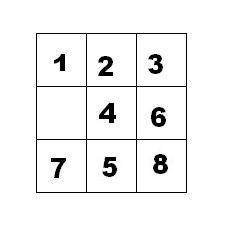
　　如下面第一个图的九宫格中，放着 1~8 的数字卡片，还有一个格子空着。与空格子相邻的格子中的卡片可以移动到空格中。经过若干次移动，可以形成第二个图所示的局面。

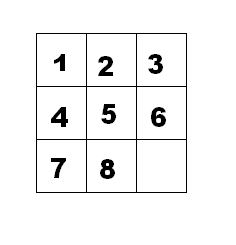
　　我们把第一个图的局面记为：12345678.
　　把第二个图的局面记为：123.46758
　　显然是按从上到下，从左到右的顺序记录数字，空格记为句点。
　　本题目的任务是已知九宫的初态和终态，求最少经过多少步的移动可以到达。如果无论多少步都无法到达，则输出-1。

输入格式

　　输入第一行包含九宫的初态，第二行包含九宫的终态。

输出格式

　　输出最少的步数，如果不存在方案，则输出-1。

样例输入

12345678.
123.46758

样例输出

3

样例输入

13524678.
46758123.

样例输出

22

思路

观察九宫格可得每个格子是空格的情况所能交换的格子情形。

bfs,队列记录每一种状态和步数，达到最终态即是最短的距离。集合进行查重。

#include<bits/stdc++.h>
using namespace std;
struct situation{
    string str;
    int pos;
    int step;
    situation(string s,int n){
        str=s;
        step=n;
        pos=getpos();
    }
    int getpos(){
        for(int i=0;i<str.size();i++){
            if(str[i]=='.'){
                return i;
            }
        }
    }
};
int dic[9][4]={{1,3},{0,2,4},{1,5},{0,4,6},{1,3,5,7},{2,4,8},{3,7},{4,6,8},{5,7}};
int dnc[9]={2,3,2,3,4,3,2,3,2};
queue<situation>q;
set<string>ss;
void bfs(string first,string target){
    q.push(situation(first,0));
    while(!q.empty()){
        situation s=q.front();
        q.pop();
        string str=s.str;
        int now=s.step;
        int pos=s.pos;
        for(int i=0;i<dnc[pos];i++){
            swap(str[pos],str[dic[pos][i]]);
            if(str==target){
                cout<<now+1<<endl;
                return ;
            }
            if(!ss.count(str)){
                ss.insert(str);
                q.push(situation(str,now+1));
            }
            swap(str[pos],str[dic[pos][i]]);
        }
    }
}
int main(){
    string a,b;
    cin>>a>>b;
    bfs(a,b);
    return 0;
}