线段树学习（segment tree)

今天在B站学习了线段树，up主讲得很清晰。

引入：我们在一个数组中如果想更新一个数据的值，记为update，所用的时间复杂度是o(1)，而求某一段区间的端点值之和，记为query，时间复杂度是o(n)。

求某一段区间的长度之和可以采用端点前缀和相减，建立一个前缀和数组，[l,r]的值等于sum[r]-sum[l-1],这样把时间复杂度降到了o(1)，可是update时间复杂度就退化为o(n)。

因为每次更新一个数据，就需要维护所有的前缀和。

由此我们引入了线段树，线段树可以实现update和query时间复杂度为o(logn)。

步骤主要有:建树、单点更新、区间查询。

首先是建树，把区间进行分隔。

 

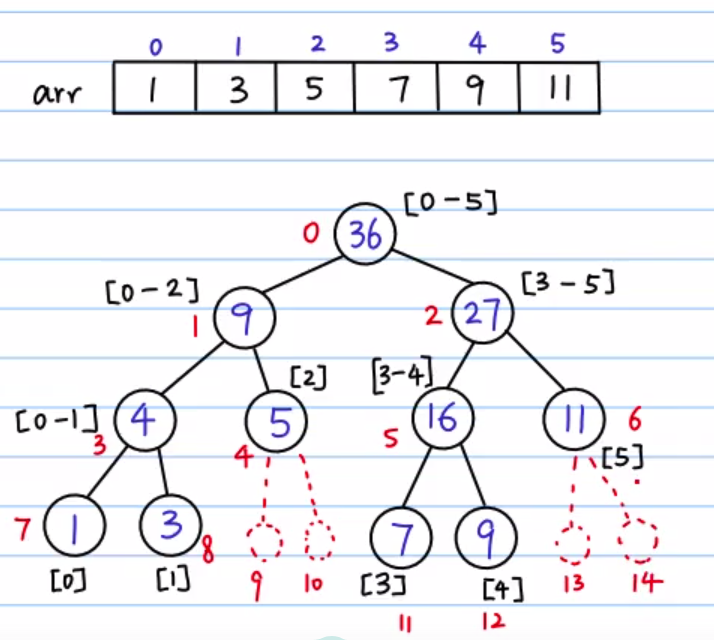
void build_node(int arr[],int tree[],int node,int start,int end)
{
    if(start==end){//递归出口
        tree[node]=arr[start];
        return;
    }
    int mid=(start+end)/2;
    int left_node=2*node+1;//左儿子对应的数组编号
    int right_node=2*node+2;//右儿子对应的数组编号
    build_node(arr,tree,left_node,start,mid);//递归左子树，区间为[start,mid]
    build_node(arr,tree,right_node,mid+1,end);//递归右子树,区间为[mid+1,end]
    tree[node]=tree[left_node]+tree[right_node];//结点值等于左右儿子相加
}

接下来是实现单点更新update的代码，将arr[4]更新为6。

 

void update_tree(int arr[],int tree[],int node,int start,int end,int idx,int val)
{
    if(start==end){
        arr[idx]=val;
        tree[node]=val;
        return ;
    }
    int mid=(start+end)/2;
    int left_node=2*node+1;
    int right_node=2*node+2;
    if(idx>=start&&idx<=mid){//如果在左分支里面
        update_tree(arr,tree,left_node,start,mid,idx,val);
    }
    else {//否则在右分支
        update_tree(arr,tree,right_node,mid+1,end,idx,val);
    }
    tree[node]=tree[left_node]+tree[right_node];
}

实现区间查询query的代码

int query_tree(int arr[],int tree[],int node,int start,int end,int L,int R)
{
    ///printf("%d %d\n", start, end);
    if(start>R||end<L)return 0;
    if(start==end||start>=L&&end<=R){
        return tree[node];
    }
    int mid=(start+end)/2;
    int left_node=node*2+1;
    int right_node=node*2+2;
    int sum_left=query_tree(arr,tree,left_node,start,mid,L,R);
    int sum_right=query_tree(arr,tree,right_node,mid+1,end,L,R);
    int sum=sum_left+sum_right;
    return sum;
}

源代码如下:

#include<bits/stdc++.h>
using namespace std;
#define MAX_LEN 1000
void build_node(int arr[],int tree[],int node,int start,int end)
{
    if(start==end){
        tree[node]=arr[start];
        return;
    }
    int mid=(start+end)/2;
    int left_node=2*node+1;
    int right_node=2*node+2;
    build_node(arr,tree,left_node,start,mid);
    build_node(arr,tree,right_node,mid+1,end);
    tree[node]=tree[left_node]+tree[right_node];
}
void update_tree(int arr[],int tree[],int node,int start,int end,int idx,int val)
{
    if(start==end){
        arr[idx]=val;
        tree[node]=val;
        return ;
    }
    int mid=(start+end)/2;
    int left_node=2*node+1;
    int right_node=2*node+2;
    if(idx>=start&&idx<=mid){
        update_tree(arr,tree,left_node,start,mid,idx,val);
    }
    else {
        update_tree(arr,tree,right_node,mid+1,end,idx,val);
    }
    tree[node]=tree[left_node]+tree[right_node];
}
int query_tree(int arr[],int tree[],int node,int start,int end,int L,int R)
{
    printf("%d %d\n", start, end);
    if(start>R||end<L)return 0;
    if(start==end||start>=L&&end<=R){
        return tree[node];
    }
    int mid=(start+end)/2;
    int left_node=node*2+1;
    int right_node=node*2+2;
    int sum_left=query_tree(arr,tree,left_node,start,mid,L,R);
    int sum_right=query_tree(arr,tree,right_node,mid+1,end,L,R);
    int sum=sum_left+sum_right;
    return sum;
}
int main()
{
    int arr[]={1,3,5,7,9,11};
    int tree[MAX_LEN]={0};
    int size=6;
    build_node(arr,tree,0,0,size-1);
    for(int i=0;i<15;i++){
        printf("tree[%d] = %d\n",i,tree[i]);
    }
    printf("\n");
    /*update_tree(arr,tree,0,0,size-1,4,6);
    for(int i=0;i<15;i++){
        printf("tree[%d] = %d\n",i,tree[i]);
    }*/
    cout<<query_tree(arr,tree,0,0,size-1,4,5)<<endl;
    return 0;
}