编译原理之文法和语言知识点汇总与Pl/0语言文法举例
一个程序设计语言是一个记号系统，如同自然语言一样，它的完整定义应包括语法和语义两个方面。所谓一个语言的语法是指一组规则，用它可以形成和产生一个合适的程序目前广泛使用的手段是上下文无关文法，即用上下文无关文法作为程序设计语言语法的描述工具。语法只是定义什么样的符号序列是合法的，与这些符号的含义毫无关系，比如对于一个 Pasca程序来说，一个上下文无关文法可以定义符号串A：=B+C是一个合乎语法的赋值语句，而A：=B+就不是。但是，如果B是实型的，而C是布尔型的，或者B、C中任何一个变量没有事先说明，则A：=B+C仍不是正确的程序，也就是说程序结构上的这种特点一类型匹配、变量作用域等是无法用上下文无关手段检查的，这些工作属于语义分析工作。程序设计语言的语义常常分为两类：静态语义和动态语义。静态语义是一系列限定规则，并确定哪些合乎语法的程序是合适的；动态语义也称作运行语义或执行语义，表明程序要做些什么，要计算什么。
字母表和符号串
字母表：符号的非空有限集合，典型的符号是字母、数字、各种标点和运算符等
符号串：定义在某一字母表上、由该字母表中的符号组成的有限符号序列
长度：长度符号串的长度是指a中出现的符号的个数，记作|α|。
空串：长度为0的符号串，常用ε表示。| ε|=0
前缀（头）：符号串α的前缀是指从符号串α的末尾删除0个或多个符号后得到的符号串。如：univ 是 university 的前缀
后缀（尾）：符号串α的后缀是指从符号串α的开头删除0个或多个符号后得到的符号串。如：sity 是 university 的后缀
子串：符号串α的子串是指删除了α的前缀和/或后缀后得到的符号串。如：ver 是 university 的子串
真前缀、真后缀、真子串：如果非空符号串β是α的前缀、后缀或子串，并且β≠α，则称β是α的真前缀、真后缀、或真子串。
子序列：符号串α的子序列是指从α中删除0个或多个符号(这些符号可以是不连续的)后得到的符号串。如：nvst
符号串运算
连接
符号串α和符号串β的连接αβ是把符号串β加在符号串α之后得到的符号串
若α=ab，β=cd，则αβ=abcd，βα=cdba。
对任何符号串α来说，都有 εα= αε = α
集合运算
字符串A与B的乘积:设A和B为符号串集合,则 A与B的乘积定义为AB={xylx∈A且y∈B}
字符串集合的正闭包:设为字母表,则, 
字符串集合的闭包(星闭包):设∑为字母表则
语言：在某一确定字母表上的特定符号串的集合。
空集，集合{ε}也是符合此定义的语言。
这个定义并没有把任何意义赋予语言中的符号串。
语言的运算
假设 L 和 M 表示两个语言
L和M的并记作L∪M：L∪M={s|s∈L 或 s∈M}
L和M的连接记作LM：LM={st|sL 并且 tM}
L的闭包记作L*：即L的0次或若干次连接。
L的正闭包记作L+：即L的1次或若干次连接。
文法：所谓文法就是描述语言的语法结构的形式规则。
任何一个文法都可以表示为一个四元组G=(VT,VN,S,φ)
VT是一个非空的有限集合，它的每个元素称为终结符号。
VN是一个非空的有限集合，它的每个元素称为非终结符号。
VT∩VN =φ
S是一个特殊的非终结符号，称为文法的开始符号。
φ是一个非空的有限集合，它的每个元素称为产生式。
BNF（Backus-Normal Form）表示法
元语言：
→ 表示 “定义为” 或 “由……组成”
<……> 表示非终结符号
| 表示“或”
算术表达式文法的BNF表示：
<表达式> → <表达式>+<项> | <表达式>-<项> | <项>
<项> → <项>*<因子> | <项>/<因子> | <因子>
<因子> → (<表达式>) | i
文法书写约定
终结符号
次序靠前的小写字母，如：a、b、c
运算符号，如：+、-、*、/
各种标点符号，如：括号、逗号、冒号、等于号
数字1、2、…、9
黑体字符串，如：id、begin、if、then
非终结符号
次序靠前的大写字母，如：A、B、C
大写字母S常用作文法的开始符号
小写的斜体符号串，如：expr、term、factor、stmt
文法符号
次序靠后的大写字母，如：X、Y、Z
终结符号串
次序靠后的小写字母，如：u、v、…、z
文法符号串
小写的希腊字母，如：a、b、g、d
推导和短语
推导：假定A→ɡ是一个产生式，α和β是任意的文法符号串，则有：αAβ→αɡβ
最左推导：如果
，并且在每“一步推导”中，都替换α中最左边的非终结符号，则称这样的推导为最左推导。
最右推导：如果，并且在每“一步推导”中，都替换α中最右边的非终结符号，则称这样的推导为最右推导。
最右推导也称为规范推导
句型、句子和语言
句型
对于文法G=(VT,VN,S,φ)，如果
，则称α是当前文法的一个句型。
句子
仅含有终结符号的句型是文法的一个句子。
语言
文法G产生的所有句子组成的集合是文法G所定义的语言，记作L(G)。
短语、直接短语和句柄
对于文法G=(VT,VN,S,φ)，假定αβ＆是文法G的一个句型，如果存在：
则称β是句型αβ＆关于非终结符号A的短语。
如果存在：
则称β是句型αβ＆关于非终结符号A的直接短语。
一个句型的最左直接短语称为该句型的句柄。
二义性
如果一个文法的某个句子有不止一棵分析树，则这个句子是二义性的句子。
含有二义性句子的文法是二义性的文法。
文法的二义性和语言的二义性
如果两个文法产生的语言相同，即L(G)=L(G¢)，则称这两个文法是等价的。
有时，一个二义性的文法可以变换为一个等价的、无二义性的文法。
有些语言，根本就不存在无二义性的文法，这样的语言称为二义性的语言。
文法分类
根据对产生式施加的限制不同，定义了四类文法和相应的四种形式语言类。
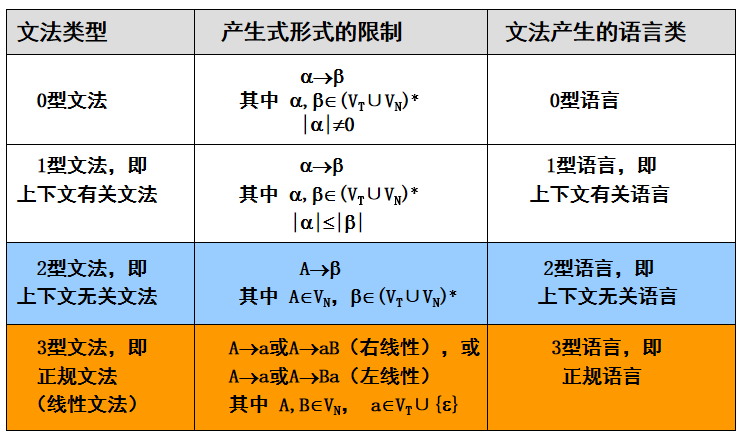
上下文无关文法及相应的语言
所定义的语法单位(或称语法实体)完全独立于这种语法单位可能出现的上下文环境
现有程序设计语言中，许多语法单位的结构可以用上下文无关文法来描述。
语言L(G)是所有包括加、减、乘、除四则运算的算术表达式的集合。
下面以Pl/0文法为例：
Pl/0语言文法的BNF表示：
〈程序〉→〈分程序〉.
〈分程序〉→ [<常量说明部分>][<变量说明部分>][<过程说明部分>]〈语句〉
<常量说明部分> → CONST<常量定义>{ ,<常量定义>};
<常量定义> → <标识符>=<无符号整数>
<无符号整数> → <数字>{<数字>}
<变量说明部分> → VAR<标识符>{ ,<标识符>};
<标识符> → <字母>{<字母>|<数字>}
<过程说明部分> → <过程首部><分程序>;{<过程说明部分>}
<过程首部> → procedure<标识符>;
<语句> → <赋值语句>|<条件语句>|<当型循环语句>|<过程调用语句>|<读语句>|<写语句>|<复合语句>|<空>
<赋值语句> → <标识符>:=<表达式>
<复合语句> → begin<语句>{;<语句>}end
<条件> → <表达式><关系运算符><表达式>|odd<表达式>
<表达式> → [+|-]<项>{<加减运算符><项>}
<项> → <因子>{<乘除运算符><因子>}
<因子> → <标识符>|<无符号整数>|(<表达式>)
<加减运符> → +|-
<乘除运算符> → *|/
<关系运算符> → =|#|<|<=|>|>=
<条件语句> → if<条件>then<语句>
<过程调用语句> → call<标识符>
<当型循环语句> → while<条件>do<语句>
<读语句> → read(<标识符>{,<标识符>})
<写语句> → write(<表达式>{,<表达式>})
<字母> → a|b|c…x|y|z
<数字> → 0|1|2…7|8|9
