CF786B Legacy （线段树优化建图模板）

gate

有向图求最短路，需要进行三种操作：

1. 点向点连边
2. 点向区间连边
3. 区间向点连边

用线段树优化建图可以解决。
建立两棵线段树，一棵存入边，一棵存出边

入边：

出边：

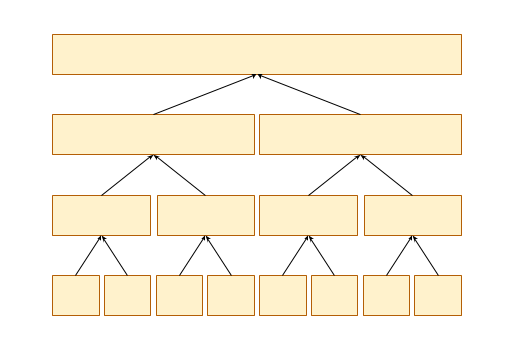
所以线段树看起来应该是这样子的：

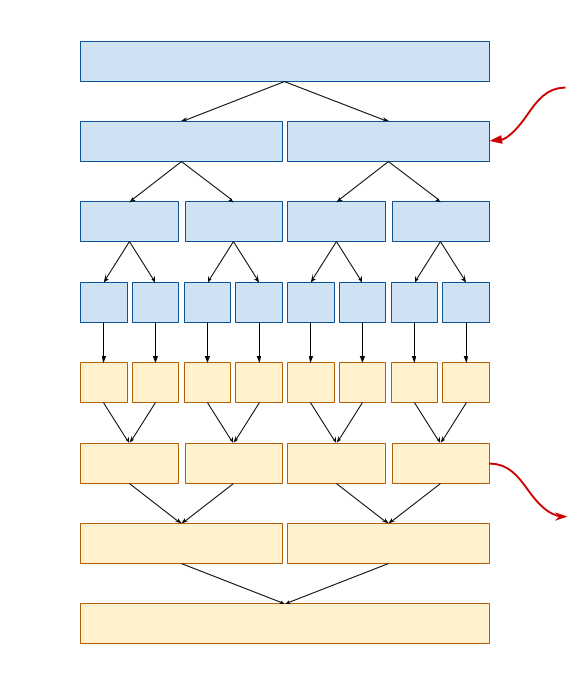
线段树内的边权为\(0\)。

code

#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
#include<vector>
#include<queue>
#define MogeKo qwq
using namespace std;

#define Mid (l+r>>1)
#define ls (now<<1)
#define rs (now<<1|1)
#define m_p make_pair

#define int long long

const int maxn =  8e5+10;
const int INF = 0x3f3f3f3f3f3f3f3f;

int n,Q,s,x,y,z,L,R,op,cnt;
int tOut[maxn],tInn[maxn];
int dis[maxn];
bool vis[maxn];
vector < pair<int,int> > e[maxn];

void build(int l,int r,int now) {
	if(l == r) {
		tOut[now] = l;
		tInn[now] = l;
		return;
	}
	int mid = Mid;
	build(l,mid,ls);
	build(mid+1,r,rs);
	tOut[now] = ++cnt;
	tInn[now] = ++cnt;
	e[tOut[ls]].push_back (m_p(tOut[now],0));
	e[tOut[rs]].push_back (m_p(tOut[now],0));
	e[tInn[now]].push_back (m_p(tInn[ls],0));
	e[tInn[now]].push_back (m_p(tInn[rs],0));
}

void updInn(int L,int R,int l,int r,int now,int x,int cost) {
	if(L == l && R == r) {
		e[x].push_back (m_p(tInn[now],cost));
		return;
	}
	int mid = Mid;
	if(R <= mid)
		updInn(L,R,l,mid,ls,x,cost);
	else if(L >= mid+1)
		updInn(L,R,mid+1,r,rs,x,cost);
	else {
		updInn(L,mid,l,mid,ls,x,cost);
		updInn(mid+1,R,mid+1,r,rs,x,cost);
	}
}

void updOut(int L,int R,int l,int r,int now,int x,int cost) {
	if(L == l && R == r) {
		e[tOut[now]].push_back (m_p(x,cost));
		return;
	}
	int mid = Mid;
	if(R <= mid)
		updOut(L,R,l,mid,ls,x,cost);
	else if(L >= mid+1)
		updOut(L,R,mid+1,r,rs,x,cost);
	else {
		updOut(L,mid,l,mid,ls,x,cost);
		updOut(mid+1,R,mid+1,r,rs,x,cost);
	}
}

void dijkstra() {
	priority_queue < pair<int,int>, vector< pair<int,int> >,greater< pair<int,int> > > q;
	memset(dis,INF,sizeof(dis));
	dis[s] = 0;
	q.push (m_p(0,s));
	while(!q.empty()) {
		int u = q.top().second;
		q.pop();
		if(vis[u]) continue;
		vis[u] = true;
		for(int i = 0; i<e[u].size(); i++) {
			int v = e[u][i].first;
			int cost = e[u][i].second;
			if(!vis[v] && dis[v] > dis[u]+cost) {
				dis[v] = dis[u] + cost;
				q.push (m_p(dis[v],v));
			}
		}
	}
}

signed main() {
	scanf("%lld%lld%lld",&n,&Q,&s);
	cnt = n;
	build(1,n,1);
	for(int i = 1; i <= Q; i++) {
		scanf("%lld",&op);
		if(op == 1) {
			scanf("%lld%lld%lld",&x,&y,&z);
			e[x].push_back (m_p(y,z));
		}
		if(op == 2) {
			scanf("%lld%lld%lld%lld",&x,&L,&R,&z);
			updInn(L,R,1,n,1,x,z);
		}
		if(op == 3) {
			scanf("%lld%lld%lld%lld",&y,&L,&R,&z);
			updOut(L,R,1,n,1,y,z);
		}
	}
	dijkstra();
	for(int i = 1; i <= n; i++)
		if(dis[i] == INF) printf("-1 ");
		else printf("%lld ",dis[i]);
	return 0;
}