2020.7.4模拟 浇花 (flower)
题目描述
\(Alice\)和\(Bob\)要传递一个\(10^9\)以内的数字。有一个\(4\times 4\)的棋盘,最开始,格子\((sx,sy)\)上有一颗棋子。一共有\(T=3600\)秒钟,每一秒之内,\(Alice\)和\(Bob\)之间的某个人可以把棋子移动到四周相邻的格子里,这个人不会不移动棋子。一个人最多连续移动\(100\)次。
交互协议
你需要实现以下两个类:
class Alice {
public :
void initA (int type ,int v ) {}
int moveA (int x ,int y ) {}
};
class Bob {
public :
void initB (int type ) {}
int moveB (int x ,int y ) {}
};
其中函数和过程的意义如下:
\(init()\)只会在交互过程开始时被交互库调用一次。
\(type\)表示数据编号,\(v\)表示要传递的数字。
\(x,y\)表示棋子目前的坐标。
返回值\((-1,-2,-3,-4)\)表示(左,右,上,下),另外\(Bob\)可以返回一个不大于\(10^9\)的正整数,使交互过程立即终止。
前置条件
- 通过判断棋子是否被移动判断另一个人是否已经操作。
传递方式
- 用四进制传递数字。

以在绿色的格子时为例。
\(Alice\)通过移到上下左右的某个位置来表示一个数字。因为不能不移动,所以一定要有两个位置,以便一个人来回移动。中间的四个格子都满足这个条件。
\(Bob\)可以通过一次移动将棋子还原到中间的四个格子之一。
最多需要\(3000\)次操作。
初始化
棋子初始可能在边角位置,且不能确定\(Alice\)和\(Bob\)谁先移动。
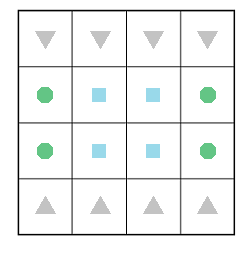
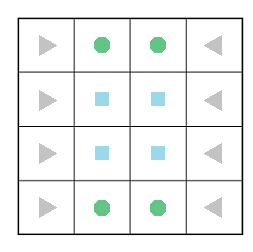
对于\(Alice\),设置规则\(1\)和规则\(2\)。
当处于三角形时,向最近的圆形或矩形移动;当处于圆形(矩形)时,向最近的矩形(圆形)移动。
\(Alice\)发现\(Bob\)移动前,采取规则\(1\)移动。
\(Alice\)发现\(Bob\)移动后,采取规则\(2\)移动。
\(Bob\)发现\(Alice\)采取规则\(2\)移动前,可以随意移动。
\(Bob\)发现\(Alice\)采取规则\(2\)移动后,将棋子移到中间的四个格子之一。
\(Alice\)在采取规则\(2\)后,再次发现\(Bob\)移动后,开始传递信息。
初始化所需的最大次数是\(400\)次(即每个人都连续移动\(100\)次)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号